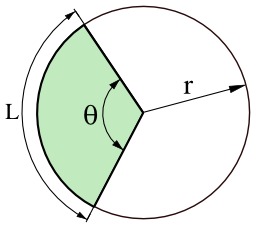
Arc de cercle

Cercle de rayon "r", arc de cercle de longueur "L" soustendu par un angle θ (theta) avec un secteur circulaire de surface "A".

→

Archimède en 1620

Archimède en 1620, par le peintre italien Domenico Feti.

→

Bas-relief de l'université d'agronomie de Pelotas au Brésil

Bas-relief de l'université d'agronomie de Pelotas au Brésil : Escola Eliseu Maciel.

→

Blason universitaire avec compas et équerre

Blason de l'Institut Parobé, Université Fédérale de Rio Grande do Sul au Brésil. Le nom Parobé est un hommage rendu à l'ingénieur João Batista Parobé, responsable de la construction de la ligne de chemin de fer Novo Hamburgo - Canela - Taquara, qui permit l'émergence et l'existence de la future commune à partir de 1903. Les premiers colonisateurs furent essentiellement des Allemands. Source : https://fr.wikipedia.org/wiki/Parob%C3%A9

→

Boussole - Compas

Boussole.

→

Cabine de planeur

Instrumentation d'un planeur moderne Schempp hirth Janus. En 2003 en France les dispositifs et les instruments d'aide au pilotage impératifs sont les suivants : l'anémomètre, sonde Pitot ou « badin » (mesure la vitesse air) en km/h ; l'altimètre (mesure l'altitude) en mètres ; le variomètre (mesure la vitesse verticale) en m/s ; le compas (indique le cap magnétique) ; la bille.

→

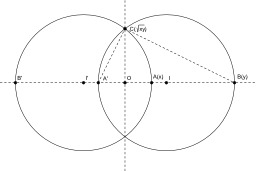
Calcul de racine carrée au compas

Construction au compas seul de la racine carrée du produit xy. Si A a pour abscisse x et B pour abscisse y, on construit les points A' et B' d'abscisses -x et -y Les cercles de diamètres [AB'] et [A'B] se coupent sur l'axe des ordonnées en un point d'ordonnée sqrt{xy} (propriété de la hauteur dans un triangle rectangle). Il est toujours possible de rabattre sqrt{xy} en abscisse par symétrie par rapport à la première bissectrice (constructible au compas).

→

Compas

→

Compas en Héraldique

Compas en Héraldique : élément pour le dessin de blasons.

→

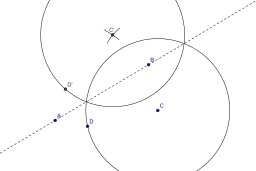
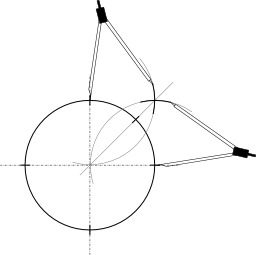
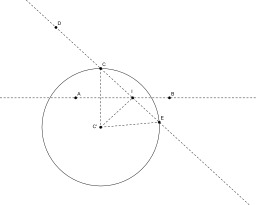
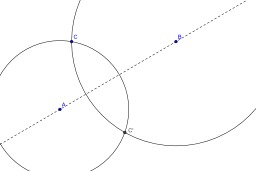
Construction au compas de l'intersection d'une droite et d'un cercle

Construction au compas seul de l'intersection d'une droite et d'un cercle (cas général) : Si la droite (AB) n'est pas un diamètre du cercle, il suffit de construire le symétrique du cercle par rapport à la droite (AB). Les points d'intersection des deux cercles sont aussi les points d'intersection du cercle de départ avec la droite (AB).

→

Construction au compas du milieu d'un segment

Construction au compas seul du milieu d'un segment : Le point A' est le symétrique de A par rapport à B. Les cercles de centre A' passant par A et de centre A passant par B se rencontrent en C et D. Le point D' est le symétrique de D par rapport à A. I est le quatrième point du parallélogramme AD'CI.

→

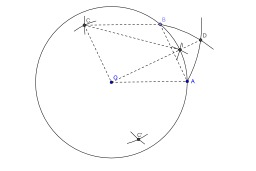
Construction d'un parallélogramme au compas

Construction au compas seul du quatrième point d'un parallélogramme : Les points A, B et C étant donnés, le quatrième point D du parallélogramme ABCD est le point d'intersection du cercle de centre A et de rayon BC et du cercle de centre C et de rayon BA non situé dans le demi-plan de frontière (CA) contenant B.

→

Construction d'une parallèle

Construction à la règle et au compas d'une parallèle à une droite passant par un point donné : La parallèle à la droite (AB) passant par un point C se construit à l'aide de la propriété de la droite des milieux. On construit le symétrique C1 du point C par rapport à A puis le symétrique C2 du point C1 par rapport à B. la droite recherchée est la droite (CC2). Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès.

→

Construction d'une perpendiculaire

Construction à la règle et au compas d'une perpendiculaire à une droite passant par une point extérieur à la droite : La perpendiculaire à la droite (AB) passant par un point C non situé sur (AB) est la droite (CC') joignant le point C à son symétrique par rapport à la droite (AB). Si le point C est situé sur (AB), il suffit de prendre le symétrique A' (ou B') du point A (ou du point B) par rapport à C, la perpendiculaire est alors la médiatrice de [AA'] (ou de [BB']).

→

Construction du milieu d'un arc au compas

Construction au compas seul du milieu d'un arc : OABC est un parallélogramme de la forme OA=OB, I est le milieu de l'arc AB de centre O, D est le point de la demi-droite [OI) telle que CA=CD, alors OD=CI. En effet, CD^2=CA^2=2CO^2+OA^2. Ensuite il suffit d'appliquer le théorème de Pythagore dans les deux triangles rectangle COI et COD : CI^2=CO^2+OI^2=CO^2+OA^2, OD^2=CD^2-CO^2=CO^2+OA^2. Or cette figure est réalisable au compas seul et permet donc de placer le point I. Si l'on suppose donnés le point O et l'arc AB, on construit le point C intersection du cercle de centre B et passant par A avec le cercle de centre O et de rayon AB. On construit de même le point C' intersection du cercle de centre A passant par O et du cercle de centre O et de rayon AB. Le point D est à l'intersection des cercles de centre C et C' et passant par A et B. Le point I est à l'intersection des cercles de centre C et C' et de rayon OD.

→

Couper un cercle en 8

Le tracé d'une bissectrice permet de définir deux arcs égaux, et ici de diviser le cercle en 8 parties égales : placer un point entre chaque point déjà placé : on place la pointe du compas sur un des points et l'on trace un arc de cercle à l'extérieur du cercle de base, et l'on fait de même sur le point voisin ; l'intersection des deux arcs définit un point. Puis, on trace à la règle le diamètre passant par ce point-là ; il coupe l'arc de cercle en deux parts égales (bissectrice de l'angle). Ainsi, si le cercle est déjà coupé en 4 parts, on en obtient 8 ; si le cercle est déjà coupé en 12 parts, on en obtient 24. On peut recouper les arcs en 2 par la même méthode, et multiplier ainsi le nombre d'arcs par 2, pour obtenir encore plus d'arcs.

→

Couper un cercle en douze parties égales

Méthode pour couper un cercle en douze parties égales en trois étapes : Avant de tracer le cercle, on trace les diamètres horizontal et vertical (droites horizontale et verticale passant par le centre) ; ce sont les « traits d'axe du cercle ». Ainsi, lorsque l'on trace le cercle, celui-ci est séparé en 4 quartiers. Pour le séparer en 12 parts égales, on place la pointe du compas sur l'intersection d'un axe et du cercle, tout en gardant un écartement égal au rayon. Puis, on trace les arcs de cercle coupant le cercle. On procède ainsi pour chaque intersection axe-cercle, on obtient au total 12 parts égales.

→

Dessin d'un cercle au compas

Dessin d'un cercle au compas.

→

Galilée à l'Université de Padoue

Félix Parra, Galilée démontre les Nouvelles Théories Astronomiques à l'Université de Padoue, 1873. Galilée est un mathématicien, géomètre, physicien et astronome italien du XVIIe siècle mort à 77 ans. Parmi ses réalisations techniques, il a inventé la lunette astronomique, perfectionnement de la découverte hollandaise d'une lunette d'approche, pour procéder à des observations rapides et précoces qui ont bouleversé les fondements de la discipline astronomique. Félix Parra (1845 - 1919) est un peintre mexicain. Source : http://fr.wikipedia.org/wiki/Galil%C3%A9e_%28savant%29

→

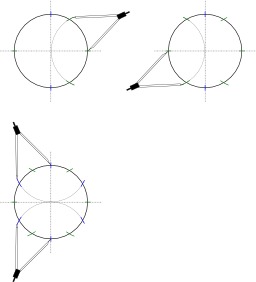
Intersection d'une droite et d'un cercle au compas

Construction au compas seul de l'intersection d'un cercle avec son diamètre : Si la droite (AB) est un diamètre du cercle, et si le point D n'est pas situé sur (AB). On construit de symétrique de D par rapport à (AB). Les deux points à chercher sont les milieux des deux arcs d'extrémités DD'.

→

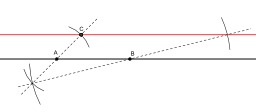
Intersection de deux droites

Construction au compas seul de l'intersection de deux droites (étape 1) : construction du point C' symétrique de C par rapport à (AB) et du point E sur (CD) tel que C'C=C'E.

→

Le fabricant de compas

Gravure extraite du livre des métiers de Jost Amman (Das Ständbuch, 1568), représentant un atelier de fabricant de compas et un client.

→

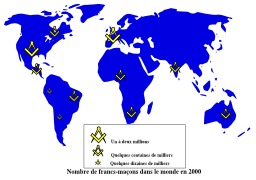
Répartition mondiale des francs-maçons en 2000

Carte du nombre de francs-maçons dans le monde en l'an 2000. Source : informations publiées dans la revue "l'histoire", n°256, juillet août 2001. Le nombre de francs-maçons en France serait erroné : selon le reportage d'"Enquêtes et révélations" diffusé sur TF1 le mardi 2 novembre 2010 à 0h20, ce nombre serait en constante augmentation, mais ne dépasserait pas les 150 000 adeptes. Logo de l'équerre et du compas : leur association symbolise une conjonction d’opposés (masculin et féminin, terrestre et céleste, matériel et spirituel), un équilibre à construire ou à maintenir. Le compas représente le ciel, alors que l’équerre représente la terre ; quand les deux symboles sont entrecroisés, microcosme et macrocosme sont imbriqués.

→

Salle de théâtre

Photo d'une salle de théâtre : The Journal Tyne Theatre

→

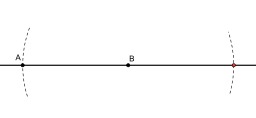
Symétrique d'un point par rapport à un point

Construction du symétrique d'un point A par rapport à un point B, à la règle et au compas.

→

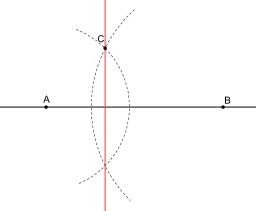
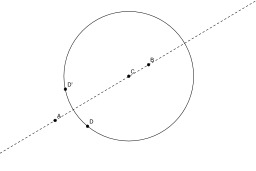
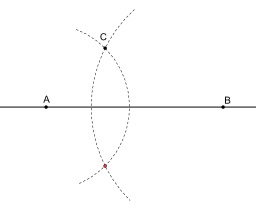
Symétrique d'un point par rapport à une droite

Construction du symétrique d'un point C par rapport à une droite à la règle et au compas : Le symétrique du point C par rapport à la droite (AB) s'obtient en construisant le point d'intersection (différent de C) entre le cercle de centre A passant par C et le cercle de centre B et passant par C. Si le point C est sur la droite (AB), il est son propre symétrique et aucune construction n'est nécessaire.

→

Symétrique d'un point par rapport à une droite

Construction au compas seul du symétrique d'un point par rapport à une droite. Le symétrique du point C par rapport à la droite (AB) est le point d'intersection des cercles de centres A et B et passant par C. Dans la construction la droite (AB) est tracée en pointillés pour permettre de suivre le raisonnement mais elle ne sert pas en tant que telle dans la construction. En géométrie classique plane, le théorème de Mohr Mascheroni, démontré par Georg Mohr en 1672 et par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas seul (sauf le tracé effectif des droites). Est considéré comme constructible tout point d'intersection de deux cercles dont les centres sont des points déjà construits et dont les rayons sont des distances entre des points déjà construits.

→

Tableau de bord aérien

Tableau de bord avec six instruments de vol : compas électro-mécanique (en bas au centre). Les 4 instruments de base en T sont complétés par, en bas à gauche l'indicateur de virage, en bas à droite le variomètre.

→

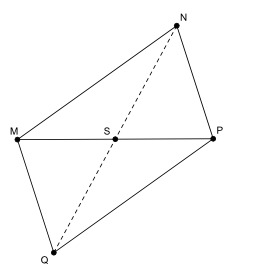
Théorème d'Apollonius

Le théorème de la médiane, ou théorème d'Apollonius, est une relation entre la longueur d'une médiane d'un triangle et la longueur de ses côtés : si S est le centre du parallélogramme, alors 2NS^2 + frac 12 MP^2 = NM^2+NP^2 2NS^2 =frac 12 NM^2+NP^2 NQ^2=NM^2+2NP^2 . Apollonios de Perga ou Apollonius de Perge (en grec ancien Ἀπολλώνιος / Apollốnios, v. 262 – v. 190 av. J.-C.) était un géomètre et astronome grec. Il serait originaire de Pergé (ou Perga, ou encore Pergè actuelle Aksu en Turquie).

→

Une leçon d'Euclide

Détail du tableau de Raphaël intitulé "L'école d'Athènes" représentant un mathématicien grec dessinant une construction géométrique avec un compas sur une ardoise posée à terre. Tableau datant de 1509 : Fresque décorant la Chambre de la signature de l'appartement de Jules II au Vatican (une des trois Stanze du musée du Vatican).

→

Une petite trousse d'écolier

Une petite trousse noire ouverte avec crayon à papier, compas, règle de 15cm et stylos à billes.

→