Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Antiquités, Antiquités grecques, noir, Rouge, Cercle, Péloponnèse (Grèce), Histoire de la guerre du Péloponnèse - Thucydide (0460?-0395? av. J.-C.), Batailles navales, Grèce (Guerre du Péloponnèse) (431-404 av. J.-C.), Patras (Grèce)
Bataille de Patras
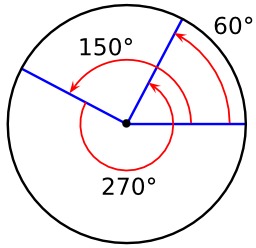
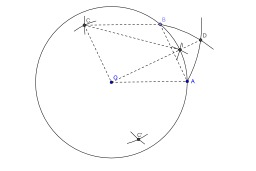
La bataille de Patras fut livrée pendant l'été 429 av. J.-C., au large de Patras, au sud de la Grèce, pendant la guerre du Péloponnèse. Les 20 trirèmes athéniennes de l'amiral Phormion y anéantirent un convoi spartiate et corinthien de 47 navires chargés d'approvisionnements destinés au troupes péloponnésiennes engagées dans la campagne d'Acarnanie. Les navires péloponnésiens, qui n'étaient pas équipés pour une bataille, se placèrent en cercle (en noir) pour mieux se défendre mais les équipages athéniens (en rouge), beaucoup plus expérimentés, manœuvrèrent afin de faire entrer en collision les navires adverses, en resserant le cercle. Quand cela arriva, avec l'aide du vent, la flotte athénienne passa à l'attaque et captura 12 navires, les autres prenant la fuite.
Cercle de pierres
Photo du cercle de pierres de Swinside en Angleterre datant de la fin du néolithique, portant le nom local de "Sunkenkirk" (église enfouie).
Cercle de pierres de Bordeaux
Photo d'un cromlech dans le jardin public de Bordeaux (Gironde). Il proviendrait du site de ''Lervaut'', près de Lesparre-Médoc.
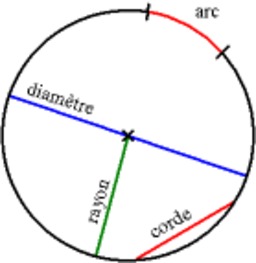
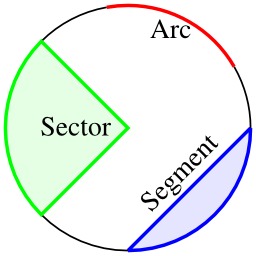
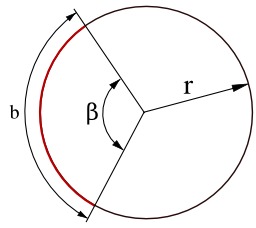
Cercle et son vocabulaire
Définition des termes géométriques concernant le cercle : arc, rayon, diamètre, corde.
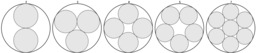
Cercles dans un cercle
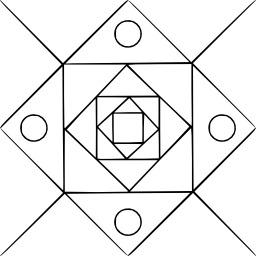
Schéma des configurations de 5 cercles avec respectivement 2, 3, 4, 5 et 7 cercles inscrits.
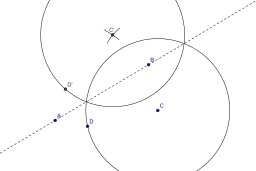
Construction au compas de l'intersection d'une droite et d'un cercle
Construction au compas seul de l'intersection d'une droite et d'un cercle (cas général) : Si la droite (AB) n'est pas un diamètre du cercle, il suffit de construire le symétrique du cercle par rapport à la droite (AB). Les points d'intersection des deux cercles sont aussi les points d'intersection du cercle de départ avec la droite (AB).
Construction du milieu d'un arc au compas
Construction au compas seul du milieu d'un arc : OABC est un parallélogramme de la forme OA=OB, I est le milieu de l'arc AB de centre O, D est le point de la demi-droite [OI) telle que CA=CD, alors OD=CI. En effet, CD^2=CA^2=2CO^2+OA^2. Ensuite il suffit d'appliquer le théorème de Pythagore dans les deux triangles rectangle COI et COD : CI^2=CO^2+OI^2=CO^2+OA^2, OD^2=CD^2-CO^2=CO^2+OA^2. Or cette figure est réalisable au compas seul et permet donc de placer le point I. Si l'on suppose donnés le point O et l'arc AB, on construit le point C intersection du cercle de centre B et passant par A avec le cercle de centre O et de rayon AB. On construit de même le point C' intersection du cercle de centre A passant par O et du cercle de centre O et de rayon AB. Le point D est à l'intersection des cercles de centre C et C' et passant par A et B. Le point I est à l'intersection des cercles de centre C et C' et de rayon OD.
Dessins et plans, Carré, Cercle, Humour, Exclamation (linguistique), Relations amoureuses, Formes (mathématiques), Mots d'esprit et jeux de mots, Odysseus, Personnages imaginaires
Hervé le carré rencontre Cléandre la ronde
Hervé le carré rencontre Cléandre la ronde, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Intersection d'une droite et d'un cercle au compas
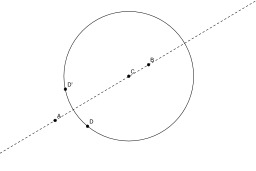
Construction au compas seul de l'intersection d'un cercle avec son diamètre : Si la droite (AB) est un diamètre du cercle, et si le point D n'est pas situé sur (AB). On construit de symétrique de D par rapport à (AB). Les deux points à chercher sont les milieux des deux arcs d'extrémités DD'.
Intersection de deux droites
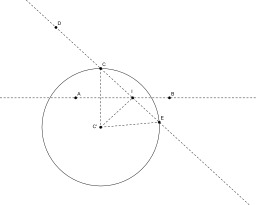
Construction au compas seul de l'intersection de deux droites (étape 1) : construction du point C' symétrique de C par rapport à (AB) et du point E sur (CD) tel que C'C=C'E.
Photographie, Dessins et plans, loup, Lièvres, Bateaux, Grenouilles, Antiquités, Gravure, Peinture, Clip art, Balles et ballons, Amphibiens, Fleurs, Géométrie, Couleurs, Accumulateurs, Piles électriques, Plages, Forêts, Sable, Parasols, Cuisine (pain), Jardinage, Jardins, Réfrigérateurs, Réfrigération et appareils frigorifiques, Bains, Bovins de boucherie, Crustacés, Cuisine -- Appareils et matériel, Nuages, Produits viticoles, feu, Linux (système d'exploitation des ordinateurs), Compas, Salades, Livres illustrés pour enfants, Ombres, laine, Poisson, Plantes des jardins, Confitures, Outillage, Pêches, Cartes à jouer, Mer, Architecture végétale des jardins, Légumes, Potages, Navires à voiles, Découpage (cuisine), Viande, Viande -- Coupe, Étoiles, Cuisine (porc), Saucisses, Enseignes, Tables (meubles), Ongle, Cuisine (aliments naturels), Thé, Bleu, Mouton (viande), soleil, Cuisine (oeufs), Peur chez les animaux, Caricatures et dessins humoristiques, noir, Mécanique, Navires, Triangle, Oeufs, Baies (fruits), Porc, Émotions, Albums à colorier, Nombres cardinaux, Éléments de cuisine, Ustensiles de cuisine, Dinde (viande), Nouvelle-Zélande -- Civilisation, Boissons non alcoolisées, Peur, Pâtisseries, Familles, Fêtes -- Accessoires, Cuisine (fromage), Gelées (confiserie), Maillots de bain, Alimentation, Ciel, Temps -- Systèmes et normes, Oeufs -- Coquilles, Poissons d'eau douce, Parents et enfants, Cuisine (poisson), Véhicules prioritaires, Poulet (viande), Râteaux, Animaux des forêts, Cheminées, Couple -- Psychologie, Espace-temps, Cuisine (sucre), Bains de soleil, Terre, Veaux, Vents, Pyramides, Couple, Graines, Filage à la main, Poissons de mer, Rouge, Aluminium, Vert, Sacs, Membres, Cercle, Navires -- Équipement, Physique, Lumière, Lumière -- Propagation, Joie, Géologie -- Cartes, Poisson rouge, Saumon rouge, Agriculture -- Outillage, Coeur, Art médiéval, Trèfles, Pyramides -- Égypte, Cristaux, Blé, Batteries, Marbre, Fillettes, Caricature, Calcaire, Plantes méditerranéennes, Géométrie euclidienne, Navigation à voile, Cuisine (légumes verts), Sacs en tissu, Pelles, Thalès, Théorème de, Seizième siècle, Dix-neuvième siècle, Dix-septième siècle, Cuivre, Grumes, Albums, Pères, Pères et filles, Sentiers, Maisons individuelles, Pattes, Refus d'obéissance, Jardins médiévaux, Lièvre d'Europe, Méditerranée (région), Cuisine (thym), Aliments crus, Parapente, Vol libre, Dix-huitième siècle, France (Révolution) (1789-1799), Albrecht Dürer (1471-1528), Vinaigre, Poisson fumé, Poisson salé, Auckland (Nouvelle-Zélande), Nouvelle-Zélande (1945-....), Aliments, Cuisine (fruits), Aliments d'origine animale, Aliments fermentés, Cuisine (légumes), Produits de l'oeuf, Boissons alcoolisées, Hérodote (0484?-0420? av. J.-C.), Circulation, Vents -- Vitesse, Métamorphisme (géologie), Savants français, Cuisine (aliments crus), Cuisine (fruits de mer), Cuisine (aliments surgelés), Volaille (viande), Cuisine (poulet), Cuisine (volaille), Produits du blé, Sirops, Sauce à salade, Cuisine (viande), Cuisine (plantes odoriférantes), Crèmes (desserts), Entremets, Poisson surgelé, Agneau (viande), Desserts, Hors-d'oeuvre, Cuisine (baies), Cuisine (vinaigre), Ondes, Cuisine (céréales), Jeux de plage, Conduits d'évacuation de fumées, Fumées, Pull-over, Bronzage, Astérides, Seaux, Serviettes, Chlorure de sodium, Cycle hercynien, Boeuf (viande), Rôtis, Rotissoires, Plats complets, Astacidés, Cuisine (écrevisses), Décapodes (crustacés), Écrevisses, Vinaigrette, Champignons cultivés, Cuisine (champignons), Cuisine (truffes), Truffe du Périgord, Tubéracées, Cassis, Cassissier, Cuisine (cassis), Aliments -- Composition, Blanquette, Cuisine (veau), Veau (viande), Veaux -- Alimentation, Omble de fontaine, Poissonneries, Saumons, Saumons -- Pêche commerciale, Cuisine (semoule), Semoule, Cônes de pin, Pignons (graines), Aliments enrichis, Cuisine (restes), Tourtes, Deux, Jeux de société, Trois, Soupes, Infusions, Lumière, Théorie ondulatoire de la, Cuisson sur réchaud de table, Fondues, Savants allemands, Jumeaux, Interférence (optique), Rhubarbe, Augustin Fresnel (1788 - 1827), Diffraction, Ondes -- Diffraction, Énergie, Photons, Temps, Mesure du, France (Chute des Girondins) ( 30 mai-2 juin 1793), Exécutions capitales et exécuteurs, France (1793), Espace de Minkowski, Relativité (physique), Cônes de lumière, Relativité générale (physique), Architecture égyptienne, Constructions en pierres sèches, Cuisine (rhubarbe), Rhubarbes, Cuisine (boeuf), Cuisines, Aliments -- Consommation, Césium, Horloges à césium, Horloges atomiques, Berne (Suisse), Échelles de temps atomique, Temps (droit international), Johannes Kepler (1571-1630), Des révolutions des orbes célestes - Nicolas Copernic (1473-1543), Héliocentrisme, Énergie éolienne en mer, Portance, Aérodynamique, Relativité restreinte (physique), Muons, Rayons cosmiques, Aquarelle, Le lièvre - Albrecht Dürer (1471-1528), Peintres allemands, Cuisine (plantes aromatiques), Résistance à la chaleur, Thymus (plantes), Abats, Cuisine (abats), Tripes, Aliments -- Réfrigération, Entreposage frigorifique, Frigidaire, Frigo, Danse maorie, Ethnologie -- Nouvelle-Zélande, Linux (logiciels), Rugby, Bayonne (Pyrénées-Atlantiques), Ferias, Aliment, Chevreau (viande), Tacuini sanitatis - al-Muẖtār ibn al-Ḥasan ibn ʿAbdūn ibn Saʿdūn Ibn Buṭlān (10..-1066?), Tangram, Corrosion, Corrosion électrochimique, Assemblages à rivets, Corrosion galvanique, Réactions chimiques -- Mécanismes, Électricité, Symétrie, Constructions géométriques, Génie mécanique, Ressorts et suspension, Ressorts, Volutes, Algues marines, Algues -- Aspect économique, Navires -- Australie, Navires -- Déchets -- Élimination, Navires océanographiques, Navires -- Règlements de sécurité, Sargasses, Mer des, Auteurs arabes, Yuwānīs Ibn Buṭlān (10..-1066?), Jardins -- Aspect symbolique, Famille -- Anthropologie, Famille -- Loisirs, Famille -- Santé et hygiène, Mouton (laine), Quenouilles, Regroupement familial, Veillées, Scènes de la vie quotidienne, Vie quotidienne, Révolution industrielle, Projection cinématographique, Signes et symboles, Carreau, Cartes à jouer, Jeux avec, Pique, Trèfle, Chaleur -- Convection, Dissipateurs thermiques (électronique), Électronique, Acides aminés, Protéines
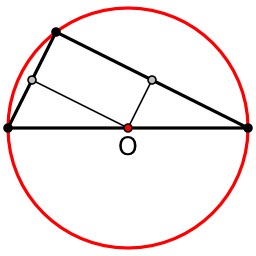
Théorème de Thalès (cercle)
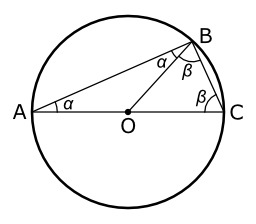
Théorème de Thalès sur le cercle. Le théorème de Thalès sur le cercle est un théorème de géométrie qui affirme qu'un triangle inscrit dans un cercle et dont un côté est un diamètre est un triangle rectangle.
Clip art, Géométrie, Triangle, Angles, Cercle, Philosophes grecs, Philosophes antiques, Thalès, Théorème de
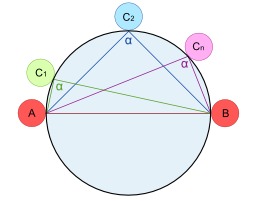
Théorème de Thalès (triangle)
Illustration du théorème de Thalès dans un demi-cercle : propriétés des angles inscrits et complémentaires.
Théorème de Thalès de Milet (triangle)
Illustration du théorème de Thalès : triangles inscrits dans un demi-cercle.
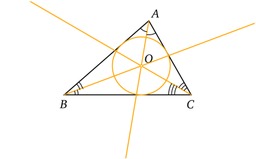
Triangle et bissectrices
Si le triangle est non plat, les trois bissectrices de ses angles (les demi-droites qui partagent les angles en deux angles de même mesure) sont concourantes en un point appelé centre du cercle inscrit, car il est le centre du seul cercle tangent aux trois côtés. Ce centre est en général noté I ou J.