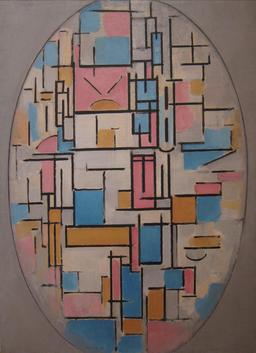Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Apiculture, Alvéoles, Giacomo Filippo Maraldi (1665-1729), Hexagone, Histoire des animaux - Aristote (0384-0322 av. J.-C.), Pappus d'Alexandrie (02..-03..)
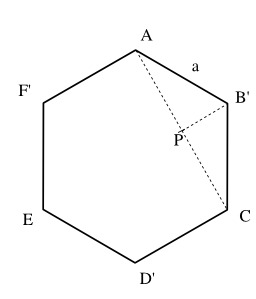
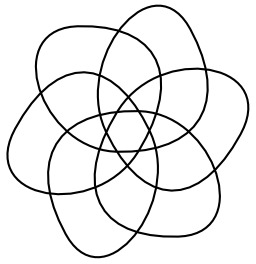
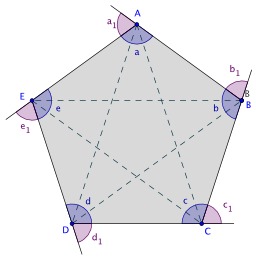
Alvéole hexagonale
Illustration pour alvéole d'abeille. La forme hexagonale des alvéoles fut repérée par Aristote dès le IVe siècle av. J.-C.(Histoire des animaux) puis traitée géométriquement huit siècles plus tard par Pappus, mathématicien grec ; mais ce n’est qu’au XVIIIe siècle que cette forme rhomboïdale fut remarquée. Ainsi, Maraldi, astronome à l’Observatoire de Paris, détermina expérimentalement en 1712 la valeur des angles de ces rhombes, égale à 109° 28′ et 70° 32′.
Photographie, Géométrie, Apiculture, Alvéoles, Gâteaux de cire, René Antoine Ferchault Réaumur (seigneur de, 1683-1757)
Alvéoles d'abeille
Intrigué par la complexité de ces formes, le physicien Réaumur soupçonne les abeilles de construire leur gâteau de cire dans un souci d’économie. Afin de vérifier son hypothèse, il demanda au géomètre allemand König de déterminer quelle était la cellule hexagonale à fond composé de trois rhombes égaux qui pouvait être construite avec le moins de matière possible.
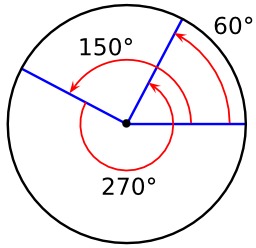
Amplitude (pendule)
Mesure de l'amplitude d'un angle de 90° par un balancier. Le balancier d’une horloge est un élément mobile animé d'un mouvement alternatif de va et vient. Il est horizontal ou circulaire au début et se nomme foliot ou balancier dans les montres actuelles. Il peut aussi prendre la forme d'un pendule, constitué d’une tige verticale, pouvant osciller autour d’un axe horizontal, et comportant un poids à son extrémité basse. Ce poids se présente généralement sous la forme d’un disque bombé, habituellement d’un métal lourd (tel que l’acier), afin de réduire l'influence des forces de résistance de l’air.
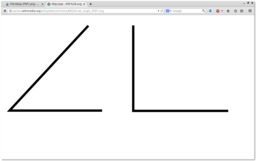
Angle aigu comparé à un angle droit
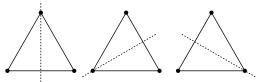
Angle aigu (à gauche) comparé à un angle droit (à droite), dessin non légendé.
Angle aigu comparé à un angle droit
Angle aigu comparé à un angle droit, traduction en francais als-33.
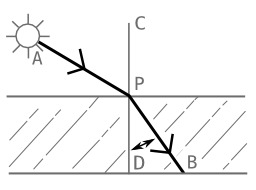
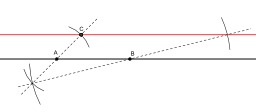
Angle de réfraction
Angle de réfraction : La réfraction, en physique des ondes — notamment en optique, acoustique et sismologie — est un phénomène de déviation d'une onde lorsque sa vitesse change entre deux milieux. La réfraction survient généralement à l'interface entre deux milieux, ou lors d'un changement de densité ou d'impédance du milieu.
Dessins et plans, Géométrie, Barcelone (Espagne), Astronomes, Dunkerque (Nord), Trigonométrie, Jean-Baptiste Delambre (1749-1822), Pierre Méchain (1744-1804), Télémètres
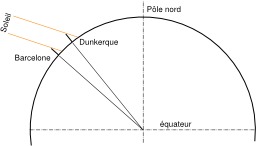
Angle Dunkerque Barcelone
Mesure de l'angle de l'arc de méridien entre Dunkerque (France) et Barcelone (Espagne) en utilisant l'ombre d'un bâton planté à la verticale. Ceci fut fait par des expéditions menées par Delambre et Méchain. Pour mesurer la distance de Dunkerque à Barcelone (qui sont sur un même méridien), on mesura la distance de proche en proche entre des points bien visibles : sommet des églises et des collines. Pour cela, on se place en un point, et on vise l'autre point, selon un principe similaire au télémètre ; la mesure des angles permet de déterminer la distance.
Dessins et plans, Géométrie, Aires (surfaces), Aires (surfaces) -- Mesure, Nombres transcendants, Pi (le nombre), British library -- Manuscrits. Papyrus 10188, Papyrus Bremner-Rhind
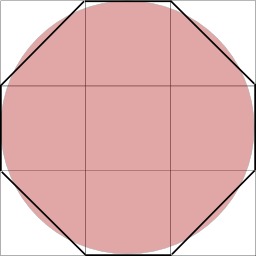
Approximation de PI par Ahmès
Illustration de l'approximation de π (PI) par Ahmès (Égypte). Découvert en 1855, le papyrus de Rhind contient le texte, recopié vers l’an 1650 avant notre ère par le scribe égyptien Ahmès, d’un manuel de problèmes pédagogiques très ancien. On y trouve une méthode pour évaluer l’aire d’un disque en prenant le carré dont le côté est égal au diamètre du disque diminué d’un neuvième. Cette méthode conduit à une évaluation de π de 256/81. Dans l’illustration ci-contre, le disque a pour diamètre 9. L’aire du disque est légèrement supérieure à l’aire de l’octogone irrégulier obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l’aire du disque est alors évaluée à 64 soit l’aire d’un carré de côté 8. Le rapport entre l’aire du disque et le carré du rayon est alors évalué par 64/(9/2)^2, c’est-à-dire 256/81.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
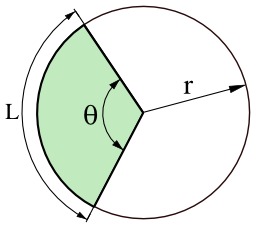
Arc de cercle
Cercle de rayon "r", arc de cercle de longueur "L" soustendu par un angle θ (theta) avec un secteur circulaire de surface "A".
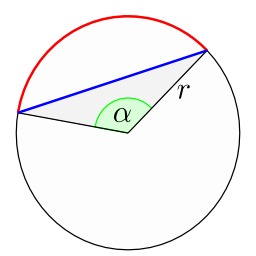
Arc et corde d'un cercle
Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Une corde (en bleu) est un segment de droite dont les extrémités se trouvent sur le cercle. Un arc est une portion de cercle délimitée par deux points (en rouge). Un secteur circulaire est une partie du disque comprise entre deux rayons. Un angle au centre (vert) est un angle formé par deux rayons du cercle.
Dessins et plans, Géométrie, Jouets de papier, Jouets, Origami, Pliages en papier, Avions en papier, Planeurs
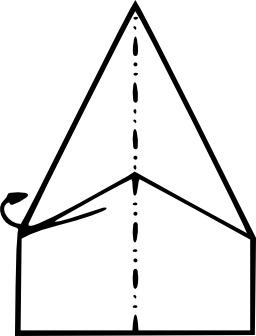
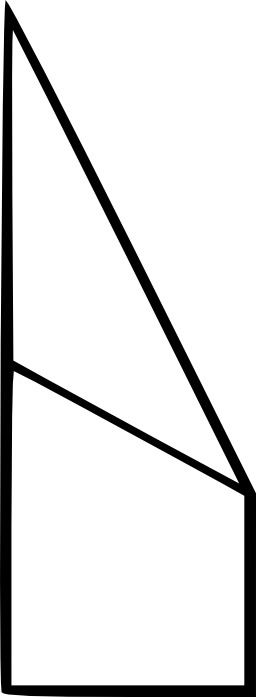
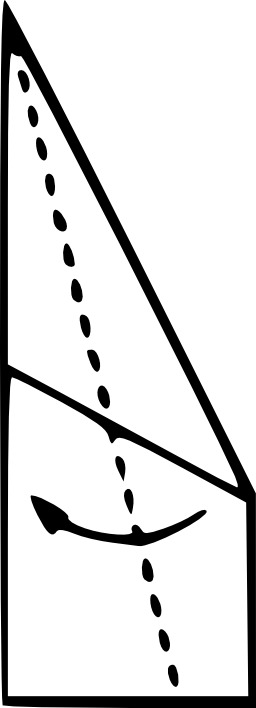
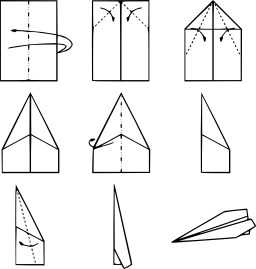
Avion de papier par pliage 10
Neuf étapes de fabrication d'un avion en papier par pliage (origami).
Photographie, Géométrie, Compas, Armoiries, Équerres, Blasons, Architecture, Bas-reliefs, Porto Alegre (Brésil)
Blason universitaire avec compas et équerre
Blason de l'Institut Parobé, Université Fédérale de Rio Grande do Sul au Brésil. Le nom Parobé est un hommage rendu à l'ingénieur João Batista Parobé, responsable de la construction de la ligne de chemin de fer Novo Hamburgo - Canela - Taquara, qui permit l'émergence et l'existence de la future commune à partir de 1903. Les premiers colonisateurs furent essentiellement des Allemands. Source : https://fr.wikipedia.org/wiki/Parob%C3%A9
Dessins et plans, Géométrie, Rubans, Bouteilles, Mathématiciens, Ferdinand Möbius (1790-1868), Felix Klein (1849-1925)
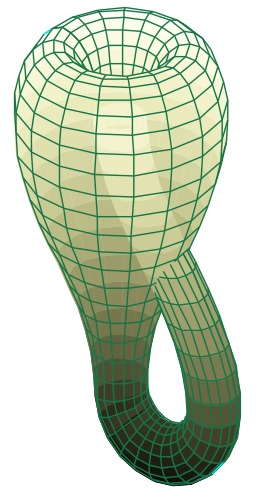
Bouteille de Klein
Vue de la bouteille de Klein dans un espace à trois dimensions. En mathématiques, la bouteille de Klein (prononcé kla.in) est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle il n'est pas possible de définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein (1849-1925). Elle est étroitement liée au ruban de Möbius.
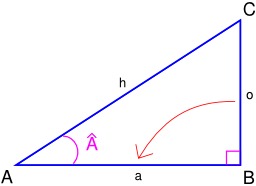
Calcul de la tangente de l'angle A
Représentation géométrique de la tangente dans un triangle rectangle. La tangente d'un angle est le rapport de la longueur du côté opposé à la longueur du côté adjacent :tan(Â) = longueur du côté opposé / longueur du côté adjacent = o/a. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique
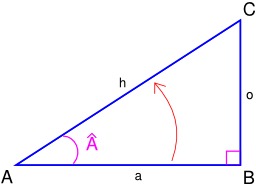
Calcul du Cosinus de l'angle A
Représentation géométrique d'un cosinus dans un triangle rectangle : Le cosinus d'un angle est le rapport de la longueur du côté adjacent par la longueur de l'hypoténuse :cos(Â) = longueur de côté adjacent / longueur de l'hypoténuse = a/h. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique
Calcul du Sinus de l'angle A
Représentation géométrique du sinus dans un triangle rectangle. Le sinus d'un angle est le rapport de la longueur du côté opposé par la longueur de l'hypoténuse :sin(Â) = longueur du côté opposé / longueur de l'hypoténuse = o/h. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
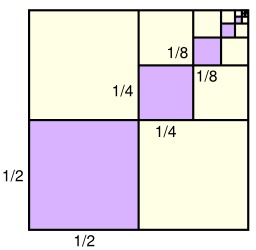
Carrés géométriques
Illustration de l'égalité 1/4 + 1/16 + 1/64 + 1/256 + ⋯ = 1/3 : chacun des carrés violets mesure 1/4 de la surface du grand carré le plus proche (1/2×1/2 = 1/4, 1/4×1/4 = 1/16, etc.). Par ailleurs, la somme des aires des carrés violets est égale à un tiers de la superficie du grand carré.
Dessins et plans, Géométrie, Tapis, Architecture -- Dessins et plans, Symétrie, Tapis persans, Art iranien, Systèmes de quadrillage, Art décoratifs, Tapis -- Cartons
Carton de tapis iranien
Angle d'un plan ("carton") de tapis iranien à formes géométriques, avec indication des couleurs, sur papier quadrillé.
Photographie, Géométrie, Tapis, Croquis (art), Symétrie, Arts décoratifs, Tapis persans, Art iranien, Tapis -- Modèles, Tapis -- Cartons
Cartons de tapis iraniens
Plans ("cartons") de tapis iraniens sur papier quadrillé avec indications de coloriage.
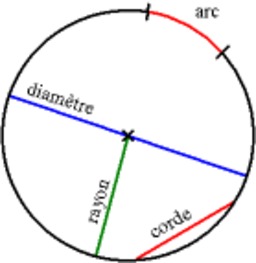
Cercle et son vocabulaire
Définition des termes géométriques concernant le cercle : arc, rayon, diamètre, corde.
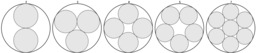
Cercles dans un cercle
Schéma des configurations de 5 cercles avec respectivement 2, 3, 4, 5 et 7 cercles inscrits.
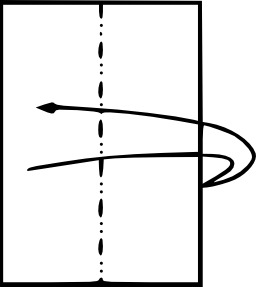
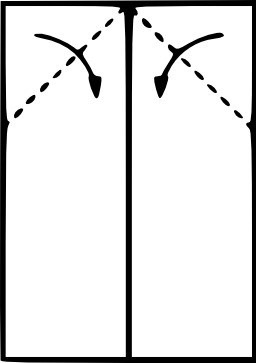
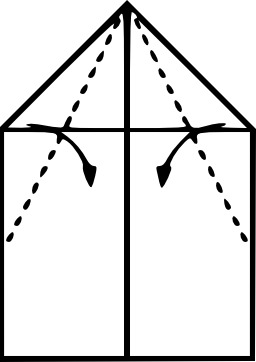
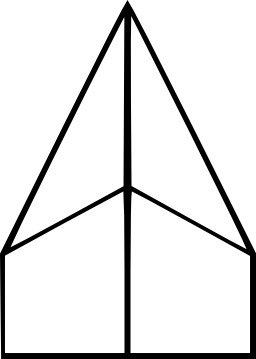
Cinq formes de tentes
Cinq formes de tentes légères : 1. géodésique, 2. dome, 3. tunnel, 4. crête, 5. pyramide. les tentes gonflables : la membrane est conçue pour se tendre sous l'action d'un gaz, celui-ci exerce une pression qui lui donne sa forme. Il s'agit ensuite de lester et de haubaner l'ensemble pour garantir une résistance optimale. Les formes obtenues sont généralement des solides gaussiens facilement concevables avec les logiciels de mise en forme 3D.
Dessins et plans, Géométrie, Bleu, Rouge, Vert, Humour, Lapins, Formes animales dans les arts décoratifs, Formes -- Aspect symbolique, Jeux géométriques
Comment dessiner un lapin
Comment dessiner un lapin avec Inkscape en utilisant trois formes et trois couleurs.
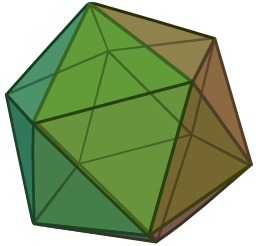
Composé polyédrique de cinq tétraèdres
Composé polyédrique de cinq tétraèdres (Wenninger modèle 25). Un composé polyédrique est un polyèdre qui est lui-même composé de plusieurs autres polyèdres partageant un centre commun, l'analogue tridimensionnel des composés polygonaux tels que l'hexagramme. Enveloppe convexe : Dodécaèdre ; Noyau : Icosaèdre ; Source : http://fr.wikipedia.org/wiki/Compos%C3%A9_poly%C3%A9drique.
Photographie, Géométrie, Illusions d'optique, Art contemporain, Art optique, Art abstrait, Op art, Pécs (Hongrie), Victor Vasarely (1908-1997)
Composition monumentale de Vasarely en Hongrie
Œuvre de Vasarely (1908-1997) devant l'église Pálosok (Pálosok templom), rue János Hunyadi (Hunyadi János utca), à Pécs, en Hongrie. Op art, ou art optique, est une expression utilisée pour décrire certaines pratiques et recherches artistiques faites à partir des années 1960, et qui exploitent la faillibilité de l'œil à travers des illusions ou des jeux optiques. Les œuvres d'op art sont essentiellement abstraites. Les pièces donnent l'impression de mouvement, d'éclat de lumière et de vibration ou de mouvements alternés. Ces sollicitations visuelles placent le corps du spectateur en situation instable, entre plaisir et déplaisir, plongé dans une sensation de vertige proche de certains états d’ivresse légère. Ce phénomène est parfois renforcé par le caractère monumental des pièces, parfois des environnements, voire dans le cas d’art opticocinétique de réelles sources de lumière jaillissant de l’ombre. Source : http://fr.wikipedia.org/wiki/Op_Art
Composition ovale avec plans en couleurs en 1914
Composition ovale avec plans en couleurs en 1914, par Piet Mondrian. Museum of Modern Art (New York).
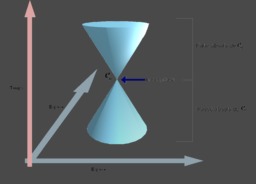
Cône de Lumière
Le cône de lumière de l'évènement e0. La flèche rose montre la dimension temporelle et les flèches grises, les dimensions spatiales. Un événement étant donné, l'ensemble des événements physiquement joignables dans le futur et de ceux du passé à partir desquels on pouvait joindre l'événement donné, forme un cône dans l'espace de Minkowski, appelé cône de lumière, et permettant des raisonnements purement géométriques par des dessins appelés diagrammes de Minkowski. Cet espace est pseudo-euclidien : bien que la métrique ne soit qu'une pseudo-métrique, les géodésiques y sont les droites, ce qui fait dire que cet espace est plat comme dans un espace euclidien. Les inégalités triangulaires qui y sont valables montrent qu'un segment est le chemin le plus long entre deux points, ce qui est une nette différence avec la géométrie euclidienne.
Dessins et plans, Géométrie, Compas, Parallèles (géométrie), Constructions géométriques, Milieux (géométrie), Segments (géométrie)
Construction au compas du milieu d'un segment
Construction au compas seul du milieu d'un segment : Le point A' est le symétrique de A par rapport à B. Les cercles de centre A' passant par A et de centre A passant par B se rencontrent en C et D. Le point D' est le symétrique de D par rapport à A. I est le quatrième point du parallélogramme AD'CI.
Dessins et plans, Géométrie, Compas, Règles, Parallèles (géométrie), Symétrie, Constructions géométriques
Construction d'une parallèle
Construction à la règle et au compas d'une parallèle à une droite passant par un point donné : La parallèle à la droite (AB) passant par un point C se construit à l'aide de la propriété de la droite des milieux. On construit le symétrique C1 du point C par rapport à A puis le symétrique C2 du point C1 par rapport à B. la droite recherchée est la droite (CC2). Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès.
Construction d'une perpendiculaire
Construction graphique de la perpendiculaire à un segment de droite quelconque.
Dessins et plans, Géométrie, Courbure, Espaces à courbure constante, Plans (géométrie), Surfaces à courbure constante
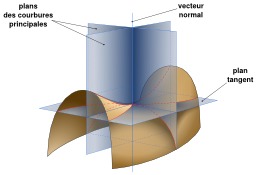
Courbures d'une surface minimale
Vue des plans définissant les courbures principales d'une surface minimale.
Découpage d'un polygone en triangles
Les triangles ont une importance capitale : en effet, tout polygone — surface délimitée par une ligne brisée fermée — peut se découper en triangles (maillage). Par ailleurs, tout triangle peut se découper en deux triangles rectangles. Ainsi, si l'on sait travailler sur un triangle rectangle, on sait travailler sur tout polygone. Par ailleurs, les triangles rectangles ont des propriétés particulières qui permettent des calculs faciles.
Dessins et plans, Géométrie, Perspective, Architecture -- Dessins et plans, Horizon, Architecture -- Dessins et plans -- Sémiotique
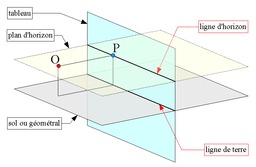
Définitions de la perspective
Schéma pour définir les termes principaux dans le domaine de la perspective en géométrie : Ligne de terre, Sol ou géométral, Plan d'horizon, Ligne d'horizon, Tableau.
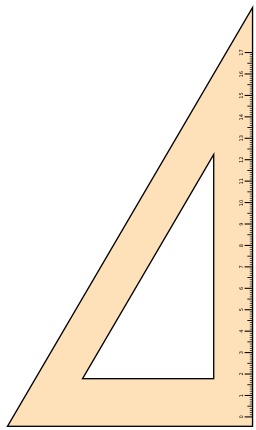
Deux équerres dos à dos
Deux équerres dos à dos, hypothénuse contre hypothénuse, formant un carré.
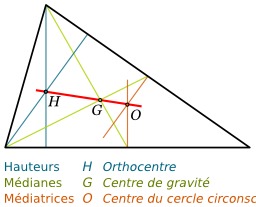
Droite d'Euler
En géométrie euclidienne, dans un triangle non équilatéral, l'orthocentre H, le centre de gravité ou isobarycentre G et le centre du cercle circonscrit \Omega sont alignés et ne sont pas confondus. On appelle droite d'Euler la droite passant par ces trois points. Traduction en français Christophe Catarina.
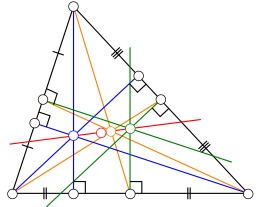
Droite d'Euler dans un triangle
En bleu : les hauteurs ; en orange : les médianes ; en vert : les médiatrices ; en rouge : la droite d'Euler. En géométrie euclidienne, dans un triangle non équilatéral, l'orthocentre H, le centre de gravité ou isobarycentre G et le centre du cercle circonscrit Omega sont alignés et ne sont pas confondus. On appelle droite d'Euler la droite passant par ces trois points.
Gravure, Géométrie, paris, Dix-neuvième siècle, Villes -- Plans, Élections, Cartographie statistique, Statistiques
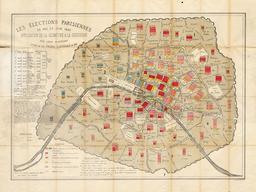
Élections parisiennes de mai et juin 1869
Les élections parisiennes de mai et juin 1869, application de la géométrie à la statistique, par Léon Montigny
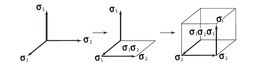
Éléments de l'algèbre géométrique
Interprétation des divers éléments d'une algèbre géométrique issue de l'espace vectoriel Euclidien 3D.
Euclide et Pythagore ou la géométrie et l'arithmétique
Euclide et Pythagore ou la géométrie et l'arithmétique (représentation au XVème siècle)
Gravure, Géométrie, Art médiéval -- Europe, Manuscrits à enluminures, Allégories -- Dans l'art, Allégories (mathématiques)
Femme enseignant la géométrie au Moyen Âge
Détail d'une enluminure du XIVe siècle, contrepoinçon d'une lettre capitale P, au début des Éléments d'Euclide, dans une traduction attribuée à Adélar de Bath. Une femme porte une équerre d'une main et utilise un compas de l'autre pour mesurer des distances sur un diagramme. Un groupe de moines, apparemment ses étudiants, la regardent. Au Moyen Âge, la représentation d'une femme dans un rôle d'enseignant est inhabituelle. La femme représentée ici serait donc plutôt une personnification de la géométrie.
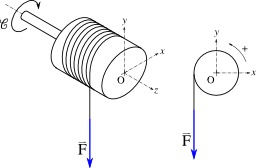
Géométrie du treuil
Géométrie d'un treuil, pour calculer le couple. En mécanique, un couple est l'effort en rotation appliqué à un axe. Il est ainsi nommé en raison de la façon caractéristique dont on obtient ce type d'action : un bras qui tire, un bras qui pousse, les deux forces étant égales et opposées. Lorsque le couple ne s'exerce pas rigoureusement dans l'axe, il se produit une rotation de cet axe (précession).
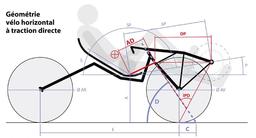
Géométrie du vélo horizontal à traction directe
Géométrie du vélo horizontal à traction directe : Un vélo couché à traction directe se différencie du vélo couché traditionnel par son pédalier, solidaire de la direction. La plupart des vélos couché sont dits "à propulsion". Leur géométrie est calquée sur celles des vélos droits, ou bicyclettes. La chaîne transmet la force du pédalier à la roue arrière, passant par toute la longueur du cadre. Si celui-ci n'est pas extrêmement rigide, une bonne partie de l'énergie fournie au pédalier est perdue. La géométrie du vélo à traction directe permet de minimiser cette perte en transmettant l'énergie à la roue avant. La conséquence est que le pédalier tourne avec la direction, nécessitant un apprentissage. L'appui sur les pédales influence la direction. On parle d'interaction pédalage/direction. Ce modèle fourni les paramètres recommandés afin d'obtenir un vélo qui soit le plus stable possible et dont l'interaction pédalage/direction soit des plus faibles. Les pourcentages indiquent l'importance de certains paramètres par rapport aux autres afin d'assurer une stabilité maximale. Plus le pourcentage est bas, moins une variation du paramètre a d'influence sur la conductabilité du vélo. La maîtrise du pilote est l'élément primordial. Une grande interaction pédalage-direction devient inexistante après plusieurs centaines de km. Respecter ces paramètres aide à avoir un vélo le plus stable possible. L'apprentissage fait le reste. En basse vitesse, c'est l'utilisateur/trice qui crée l'équilibre. A haute vitesse, les forces auto-stabilisantes sont prépondérantes. Un appui naturel de la jambe part du fémur du même côté. Pour que la force passe par l'axe D et ainsi annuler l'interaction PD, il faut inverser cet appui. Lorsque la jambe droite appuie, c'est la hanche côté gauche qui reçoit l'appui.
Gravure, Géométrie, Versailles (Yvelines) -- Château, Surfaces (mathématiques) -- Volumes, Allain Manesson-Mallet (1630-1706)
Géométrie pratique en 1702
Formes géométriques surmontées d'une vue de la Petite Écurie, où Manesson Mallet enseignait les mathématiques. "Des cylindres, hémisphères, colonnes, segmens, ou portions de sphères, cônes, etc." par Allain Manesson-Mallet, La Géométrie pratique, t. I, Paris, Anisson, 1702. (Géométrie pratique, t. 1, planche XXXIX).
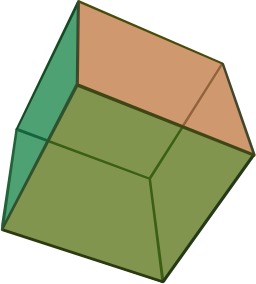
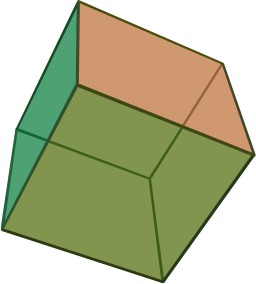
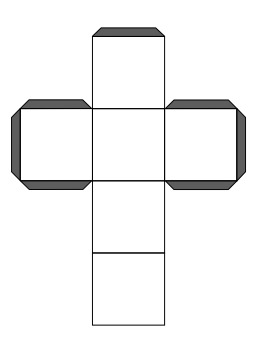
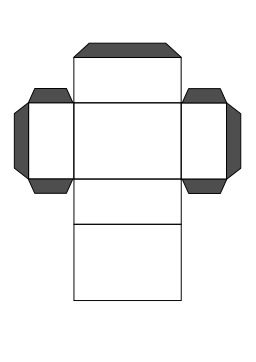
Hexaèdre régulier, le cube
En géométrie des solides, un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube. Le terme hexaèdre vient du grec heksaedros et du bas latin hexahedrum, ce qui justifie la présence de la lettre h dans la traduction anglaise "hexahedron".
Intersection de deux droites
Construction au compas seul de l'intersection de deux droites (étape 1) : construction du point C' symétrique de C par rapport à (AB) et du point E sur (CD) tel que C'C=C'E.
Photographie, Géométrie, Architecture des jardins, Architecture végétale des jardins, Podensac (Gironde. - région), Sauternes (Gironde), Vignobles, Géométrie de la ligne, Perspective
Jardin dans un vignoble
Photographie des jeux de ligne entre jardin et paysage du vignoble du Sauternais, entre minéral et végétal. Malle à Preignac-33.
Dessins et plans, Géométrie, Perspective, Espace (architecture), Espace (art), Géométrie de l'espace, Images tridimensionnelles, Vues perspectives
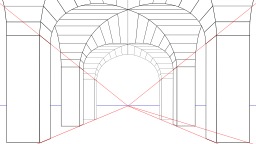
Lois de la perspective
Perspective avec lignes de fuite et point de fuite. La perspective est l'ensemble des lois permettant de représenter sur un plan des figures à trois dimensions. En art, notamment en peinture et en architecture, il faudrait parler des perspectives : diverses méthodes ont été utilisées pour donner l'illusion de la réalité tridimensionnelle.
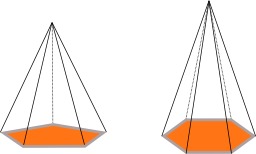
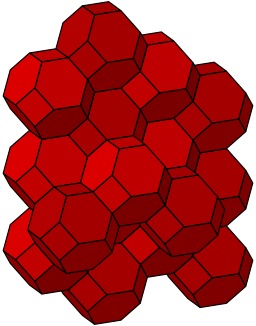
Nids d'abeille partiels
En géométrie, les polyèdres obliques infinis sont une définition étendue des polyèdres, créés par des faces polygonales régulières, et des figures de sommet non planaires. Beaucoup sont directement reliés aux nids d'abeille convexes uniformes, étant la surface polygonale d'un nid d'abeille avec certaines cellules enlevées. En tant que solides, ils sont appelés nids d'abeille partiels et aussi éponges. Ces polyèdres sont aussi appelés pavages hyperboliques parce qu'ils peuvent être regardés comme reliés aux pavages de l'espace hyperbolique qui ont aussi un défaut angulaire négatif.
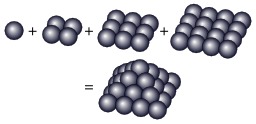
Nombre pyramidal carré 30
Représentation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16.
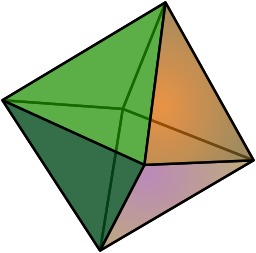
Octaèdre régulier
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces, notamment l'octaèdre régulier. Un octaèdre dont toutes les faces sont triangulaires, possède alors douze arêtes et six sommets.
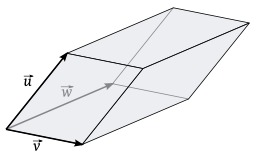
Parallélépipède déterminé par trois vecteurs
Parallélépipède déterminé par trois vecteurs. En géométrie dans l'espace, les parallélépipèdes sont des hexaèdres dont les faces sont parallèles deux à deux.
Photographie, Dessins et plans, Géométrie, Carré, rectangle, rectangles, Angles, Parallèles (géométrie), Parallélogrammes, Polygones, Tablettes d'argile cunéiformes, Pentagones, Diagonales, Racine carrée de deux, Losanges, Quadrilatères, Trapèzes, Aires (surfaces), Aires (surfaces) -- Mesure
Parallélograme
Exemple de parallélogramme. Un parallélogramme, en géométrie, est un quadrilatère dont les côtés opposés sont parallèles deux à deux
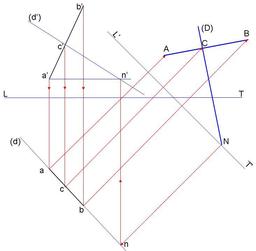
Perspective cavalière à 90°
Comparaison entre les projections orthogonales sur les plans contenant les axes (géométrie descriptive) et la perspective cavalière : report des coordonnées. Pour effectuer une représentation en perspective cavalière, il faut choisir différents paramètres : 1) un plan frontal : un segment contenu dans ce plan, ou dans un plan parallèle, est représenté en vraie grandeur ; 2) un angle de fuite : les perpendiculaires au plan frontal, appelées fuyantes sont représentées dans cette direction ; 3) un coefficient de réduction : les longueurs représentées dans la direction de fuite sont multipliées par ce coefficient de réduction. De plus, l'alignement des points, le parallélisme des droites le rapport des longueurs de deux segments parallèles, et donc les milieux, sont conservés. En revanche, les longueurs, les aires, et les angles ne sont pas conservés dans les plans non frontaux. Les éléments cachés par les faces supposées opaques sont représentés en pointillés; les éléments visibles par l'observateur sont représentés en traits pleins.
Portrait de Gaspard Monge
Le tour de la France par deux enfants, par George Bruno, pseudonyme d'Augustine Fouillée (née Tuillerie), 1877, p.108 ; manuel scolaire, édition de 1904 : Gaspard MONGE (1746-1818), mathématicien français dont l'œuvre considérable mêle géométrie descriptive, analyse infinitésimale et géométrie analytique. En parallèle à ses travaux de recherche, il enseigne une grande partie de sa vie et a comme élèves beaucoup des futurs grands mathématiciens français du XIXe siècle. Il joue un grand rôle dans la Révolution française, tant du point de vue politique que du point de vue de l'instauration d'un nouveau système éducatif : il participe à la création de l'École normale de l'an III et de l'École polytechnique (en 1794), deux écoles où il enseigne la géométrie. Il concourt également avec Berthollet, Chaptal et Laplace à la création de l'École d'arts et métiers. Il est également membre de la commission des sciences et des arts lors de la campagne d'Italie (1796-1797), et chargé de mission dans l'expédition d'Égypte (1798-1799). Le 12 décembre 1989, ses cendres ont été transférées au Panthéon.
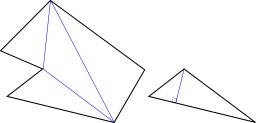
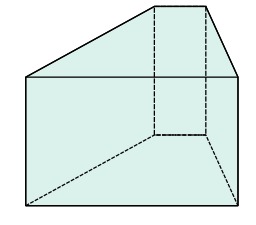
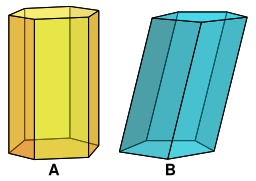
Prisme droit et prisme oblique
Prisme droit (A, jaune) et prisme oblique (B, bleu). Lorsque le plan est perpendiculaire à la droite génératrice (d), le prisme est appelé prisme droit. Lorsque le prisme est droit, les faces latérales sont des rectangles.