Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
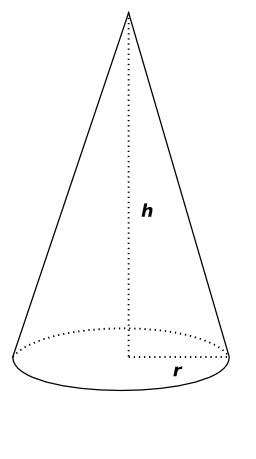
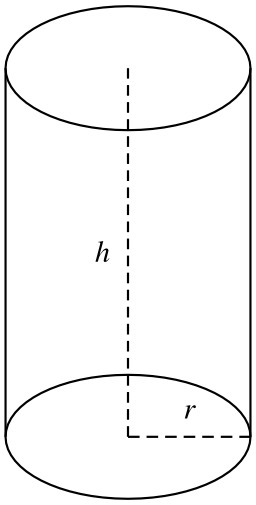
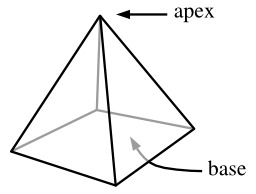
Cône de révolution
Cône de révolution avec son rayon et sa hauteur : illustré par le cornet à glace ou le chapeau de clown.
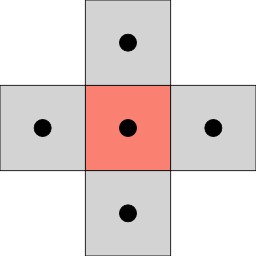
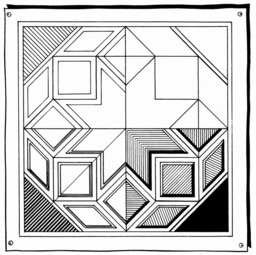
Connectivité du carré
Dans le cadre des pavages, la connectivité géométrique indique la relation entre un élément de pavage (une case ou tuile) et ses voisins. On parlera de 4-connectivité lorsqu'une case (ici un carré) comporte 4 voisins directs.
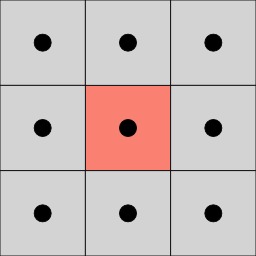
Connectivité du carré
Dans le cadre des pavages, la connectivité géométrique indique la relation entre un élément de pavage (une case ou tuile) et ses voisins. On parlera de 8-connectivité lorsqu'une case (ici un carré) comporte 8 voisins directs.
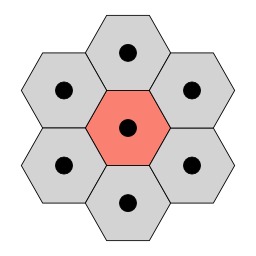
Connectivité hexagonale
Dans le cadre des pavages, la connectivité géométrique indique la relation entre un élément de pavage (une case ou tuile) et ses voisins. On parlera de 6-connectivité lorsqu'une case (ici un hexagone) comporte 6 voisins directs.
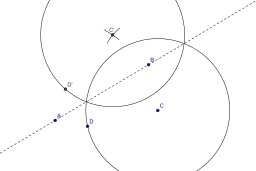
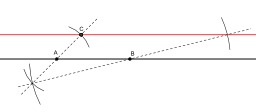
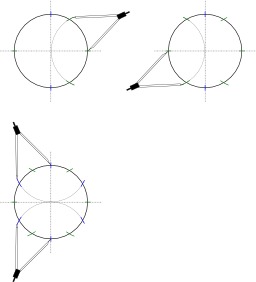
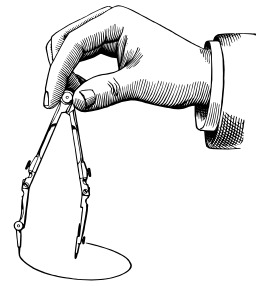
Construction au compas de l'intersection d'une droite et d'un cercle
Construction au compas seul de l'intersection d'une droite et d'un cercle (cas général) : Si la droite (AB) n'est pas un diamètre du cercle, il suffit de construire le symétrique du cercle par rapport à la droite (AB). Les points d'intersection des deux cercles sont aussi les points d'intersection du cercle de départ avec la droite (AB).
Dessins et plans, Géométrie, Compas, Parallèles (géométrie), Constructions géométriques, Milieux (géométrie), Segments (géométrie)
Construction au compas du milieu d'un segment
Construction au compas seul du milieu d'un segment : Le point A' est le symétrique de A par rapport à B. Les cercles de centre A' passant par A et de centre A passant par B se rencontrent en C et D. Le point D' est le symétrique de D par rapport à A. I est le quatrième point du parallélogramme AD'CI.
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
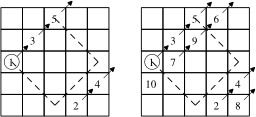
Construction d'un carré magique par la méthode du losange - 1
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
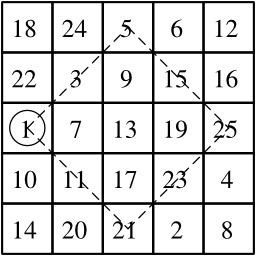
Construction d'un carré magique par la méthode du losange - 2
Un carré magique 5x5 construit selon la méthode du losange proposée par John Horton Conway : Le résultat final est un carré magique dont la constante est 65.
Construction d'un parallélogramme au compas
Construction au compas seul du quatrième point d'un parallélogramme : Les points A, B et C étant donnés, le quatrième point D du parallélogramme ABCD est le point d'intersection du cercle de centre A et de rayon BC et du cercle de centre C et de rayon BA non situé dans le demi-plan de frontière (CA) contenant B.
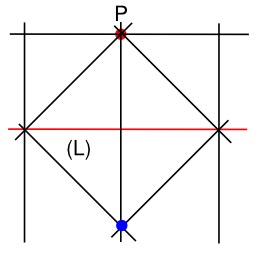
Construction d'un point symétrique par pliage
Construction du symétrique d'un point par rapport à une droite par origami : On construit la perpendiculaire à (L) passant par P puis la perpendiculaire à cette perpendiculaire passant par P (autrement dit, la parallèle à (L) passant par P). On construit les deux bissectrices en P à la parallèle à (L) et la perpendiculaire à (L). Ces deux bissectrices vont couper (L) en deux points d'où l'on trace deux nouvelles perpendiculaires à (L). Deux dernières bissectrices vont se couper en le symétrique à P cherché.
Dessins et plans, Géométrie, Compas, Règles, Parallèles (géométrie), Symétrie, Constructions géométriques
Construction d'une parallèle
Construction à la règle et au compas d'une parallèle à une droite passant par un point donné : La parallèle à la droite (AB) passant par un point C se construit à l'aide de la propriété de la droite des milieux. On construit le symétrique C1 du point C par rapport à A puis le symétrique C2 du point C1 par rapport à B. la droite recherchée est la droite (CC2). Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès.
Dessins et plans, Géométrie, Compas, Règles, Constructions géométriques, Médiatrices, Perpendiculaires
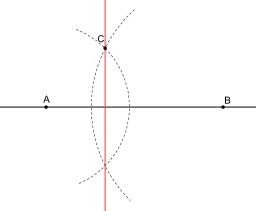
Construction d'une perpendiculaire
Construction à la règle et au compas d'une perpendiculaire à une droite passant par une point extérieur à la droite : La perpendiculaire à la droite (AB) passant par un point C non situé sur (AB) est la droite (CC') joignant le point C à son symétrique par rapport à la droite (AB). Si le point C est situé sur (AB), il suffit de prendre le symétrique A' (ou B') du point A (ou du point B) par rapport à C, la perpendiculaire est alors la médiatrice de [AA'] (ou de [BB']).
Construction d'une perpendiculaire
Construction graphique de la perpendiculaire à un segment de droite quelconque.
Construction du milieu d'un arc au compas
Construction au compas seul du milieu d'un arc : OABC est un parallélogramme de la forme OA=OB, I est le milieu de l'arc AB de centre O, D est le point de la demi-droite [OI) telle que CA=CD, alors OD=CI. En effet, CD^2=CA^2=2CO^2+OA^2. Ensuite il suffit d'appliquer le théorème de Pythagore dans les deux triangles rectangle COI et COD : CI^2=CO^2+OI^2=CO^2+OA^2, OD^2=CD^2-CO^2=CO^2+OA^2. Or cette figure est réalisable au compas seul et permet donc de placer le point I. Si l'on suppose donnés le point O et l'arc AB, on construit le point C intersection du cercle de centre B et passant par A avec le cercle de centre O et de rayon AB. On construit de même le point C' intersection du cercle de centre A passant par O et du cercle de centre O et de rayon AB. Le point D est à l'intersection des cercles de centre C et C' et passant par A et B. Le point I est à l'intersection des cercles de centre C et C' et de rayon OD.
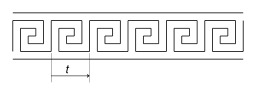
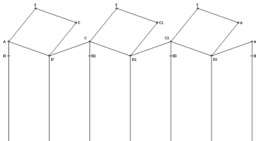
Construction géométrique d'une frise
Exemple de frise géométrique avec son vecteur de translation.
Dessins et plans, Géométrie, Drapeaux, Douze (le nombre), Pays de l'Union européenne, Histoire, Europe
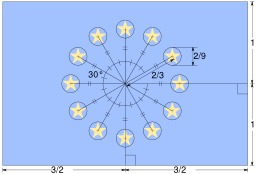
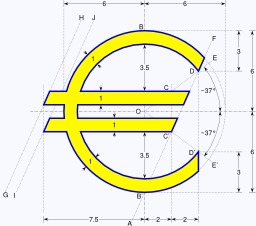
Construction géométrique du drapeau de l'Europe
Construction géométrique du drapeau de l'Europe : Le drapeau est rectangulaire avec une proportion de 2:3. Il est composé d'un cercle de douze étoiles d'or sur un champ d'azur. Toutes les étoiles sont disposées verticalement (la pointe vers le haut), ont cinq branches et sont espacées de façon égale selon les positions des heures sur cadran d'une horloge. Chaque rayon d'étoile est égal à un dix-huitième de la hauteur du guindant. La description héraldique officielle donnée par l'Union européenne est : « Le drapeau européen est représenté par un cercle de douze étoiles d'or sur fond bleu. Les étoiles symbolisent les idéaux d'unité, de solidarité et d'harmonie entre les peuples d'Europe. »
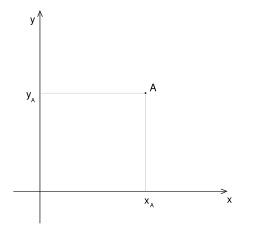
Coordonnées cartésiennes
En coordonnées cartésiennes planaires, la position d'un point A est donnée par les distances xA et yA. Le mot cartésien vient du mathématicien et philosophe français René Descartes.
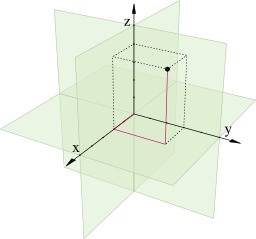
Coordonnées cartésiennes tridimensionnelles
En coordonnées cartésiennes tridimensionnelles, la position d'un point est donnée par les distances aux axes x, y et z.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas, Compas,
Couper un cercle en 8
Le tracé d'une bissectrice permet de définir deux arcs égaux, et ici de diviser le cercle en 8 parties égales : placer un point entre chaque point déjà placé : on place la pointe du compas sur un des points et l'on trace un arc de cercle à l'extérieur du cercle de base, et l'on fait de même sur le point voisin ; l'intersection des deux arcs définit un point. Puis, on trace à la règle le diamètre passant par ce point-là ; il coupe l'arc de cercle en deux parts égales (bissectrice de l'angle). Ainsi, si le cercle est déjà coupé en 4 parts, on en obtient 8 ; si le cercle est déjà coupé en 12 parts, on en obtient 24. On peut recouper les arcs en 2 par la même méthode, et multiplier ainsi le nombre d'arcs par 2, pour obtenir encore plus d'arcs.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
Couper un cercle en douze parties égales
Méthode pour couper un cercle en douze parties égales en trois étapes : Avant de tracer le cercle, on trace les diamètres horizontal et vertical (droites horizontale et verticale passant par le centre) ; ce sont les « traits d'axe du cercle ». Ainsi, lorsque l'on trace le cercle, celui-ci est séparé en 4 quartiers. Pour le séparer en 12 parts égales, on place la pointe du compas sur l'intersection d'un axe et du cercle, tout en gardant un écartement égal au rayon. Puis, on trace les arcs de cercle coupant le cercle. On procède ainsi pour chaque intersection axe-cercle, on obtient au total 12 parts égales.
Dessins et plans, Géométrie, Courbure, Espaces à courbure constante, Plans (géométrie), Surfaces à courbure constante
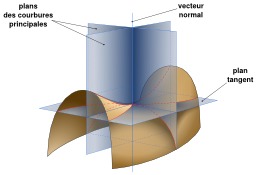
Courbures d'une surface minimale
Vue des plans définissant les courbures principales d'une surface minimale.
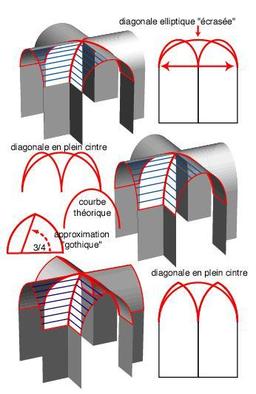
Croisée d'ogives
Genèse de la croisée d'ogives. La projection orthogonale de cette croisée selon l’axe de chacune des nefs donne une demi-ellipse posée dans sa hauteur, très résistante en son sommet. Par chance, il existe une bonne approximation de cet arc pour cette époque où, sur le chantier, à défaut de bons moyens de calcul et de mesures précises il vaut mieux recourir à des tracés simples à exécuter : il s’agit d'un arc brisé composé de deux arcs de cercle centrés respectivement au premier et au troisième quart de la distance à franchir. Cette approximation est souvent observable à une légère déformation de la voûte de la croisée à l'endroit où elle se raccorde aux nefs.
Découpage d'un polygone en triangles
Les triangles ont une importance capitale : en effet, tout polygone — surface délimitée par une ligne brisée fermée — peut se découper en triangles (maillage). Par ailleurs, tout triangle peut se découper en deux triangles rectangles. Ainsi, si l'on sait travailler sur un triangle rectangle, on sait travailler sur tout polygone. Par ailleurs, les triangles rectangles ont des propriétés particulières qui permettent des calculs faciles.
Dessins et plans, Géométrie, Perspective, Architecture -- Dessins et plans, Horizon, Architecture -- Dessins et plans -- Sémiotique
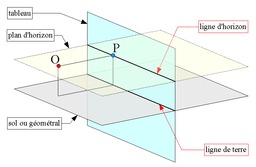
Définitions de la perspective
Schéma pour définir les termes principaux dans le domaine de la perspective en géométrie : Ligne de terre, Sol ou géométral, Plan d'horizon, Ligne d'horizon, Tableau.
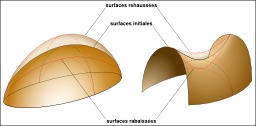
Déformation de surfaces
Vue de l'influence des déformations de surfaces sur une surface convexe et une autre en forme de selle (surface minimale).
Photographie, Géométrie, Antiquités gallo-romaines, Dessin, Dessin d'architecture, Bordeaux (Gironde), Mosaïques, Burdigala (ville ancienne), sylvanus-aquitaine
Dessin de la grande mosaïque géométrique de Burdigala
Dessin de la grande mosaïque géométrique de Burdigala, Musée d'Aquitaine, Bordeaux.
Dessin de lapin couché
Dessin de lapin couché réalisé avec Inskape : trois formes géométriques et trois couleurs.
Gravure, Géométrie, Vues, Perspective, Walter Crane (1845-1915), Perception du volume, Perception des paysages, Arts décoratifs, Tutoriels, Dessin -- Étude et enseignement
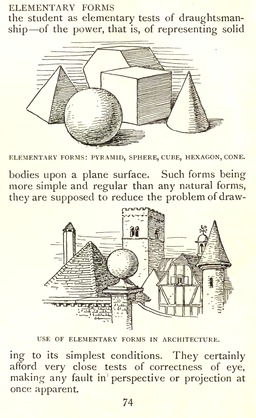
Dessin de volumes et perspective
Walter Crane, Line and Form, page 74 : Dessin de volumes et respect de la perspective.
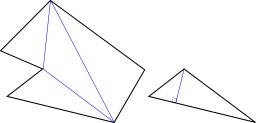
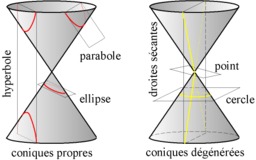
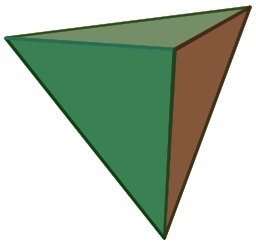
Deux types de coniques
Les coniques propres, quand le plan de coupe ne passe pas par le sommet du cône ; les coniques dégénérées, quand le plan contient le sommet du cône.
Gravure, Géométrie, Lecture, Écriture, Disques durs, Informatique, Informatique -- Appareils et matériel, Capacité totale, Disques magnétiques, Ordinateurs -- Mémoires, Ordinateurs -- Mémoires magnétiques, Stockage
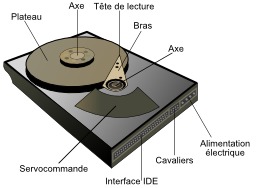
Disque dur
Schéma des composants du disque dur (légendé en français par historicair) : plateau, axe, tête de lecture, bras, alimentation électrique, interface IDE (SATA), servocommande, cavalier.
Dessins et plans, Géométrie, Cauchy (Augustin Louis, baron), 1789-1857, Dodécaèdres, Polyèdres, Projection stéréographique
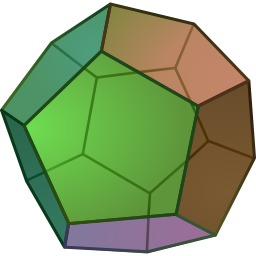
Dodécaèdre
Le dodécaèdre, un polyèdre régulier convexe. En 1811, Cauchy (1789-1857) s’intéresse dans son premier mémoire à l’égalité de polyèdres convexes dont les faces sont égales. Il propose une démonstration du théorème de Descartes-Euler, concernant les nombres de sommets, de faces et d'arêtes d'un polyèdre convexe. Sa preuve consiste à projeter le polyèdre en un graphe planaire suivant ce qui est aujourd’hui appelé une projection stéréographique. Cependant, Cauchy commit une erreur, en ne faisant pas d’hypothèse claire sur les polyèdres étudiés. Dans son second mémoire en 1812, il donna des formules pour calculer les angles diédraux.
Dodécaèdre romain
Un dodécaèdre romain est un petit objet creux de bronze ou de pierre en forme de dodécaèdre régulier à 12 faces pentagonales ayant chacune un trou circulaire en son centre. Ces objets datent du second au troisième siècle après J.-C. Source : http://fr.wikipedia.org/wiki/Dod%C3%A9ca%C3%A8dre_romain
Dôme sphérique
Dôme de la Grande mosquée de Kairouan. Usage de la sphère en architecture : voûte demi-sphérique côtelée d'un dôme de la Grande Mosquée de Kairouan (en Tunisie).
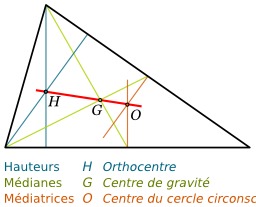
Droite d'Euler
En géométrie euclidienne, dans un triangle non équilatéral, l'orthocentre H, le centre de gravité ou isobarycentre G et le centre du cercle circonscrit \Omega sont alignés et ne sont pas confondus. On appelle droite d'Euler la droite passant par ces trois points. Traduction en français Christophe Catarina.
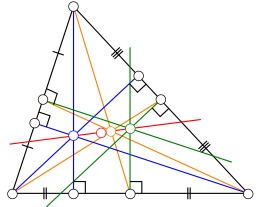
Droite d'Euler dans un triangle
En bleu : les hauteurs ; en orange : les médianes ; en vert : les médiatrices ; en rouge : la droite d'Euler. En géométrie euclidienne, dans un triangle non équilatéral, l'orthocentre H, le centre de gravité ou isobarycentre G et le centre du cercle circonscrit Omega sont alignés et ne sont pas confondus. On appelle droite d'Euler la droite passant par ces trois points.
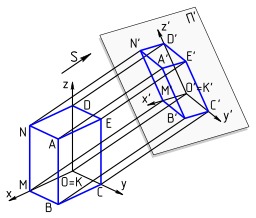
Projection axonométrique
Principe de l'axonométrie : le pavé se projette sur le plan Π' selon la direction S, l'image obtenue est une perspective axonométrique du pavé.
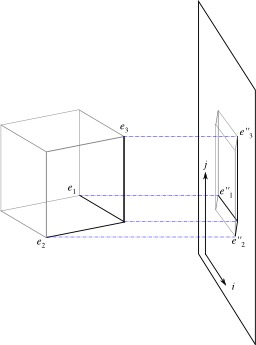
Projection orthogonale
La projection orthogonale est un type de perspective très utilisée en dessin (géométrie descriptive), et en infographie : la génération des figures est simple, par contre, on ne peut pas représenter l'éloignement (la taille des objets ne varie pas avec la distance). De manière plus générale, en algèbre linéaire, une projection orthogonale est un projecteur tel que les deux sous-espaces sont orthogonaux. La projection orthogonale permet de résoudre le problème de la plus courte distance d'un point à une droite, d'un point à un plan, ou plus généralement d'un point à un sous-espace affine d'un espace euclidien d'autre part. On peut alors utiliser ce concept pour résoudre des problèmes de type «moindres carrés». L'idée générale, basée sur le théorème de Pythagore, est que le problème de plus courte distance se ramène à une propriété d'orthogonalité.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
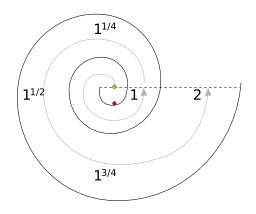
Puissance d'un point
En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
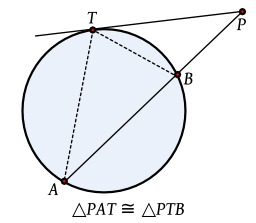
Puissance d'un point
Détermination de la valeur algébrique de la puissance d'un point extérieur à un cercle. En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
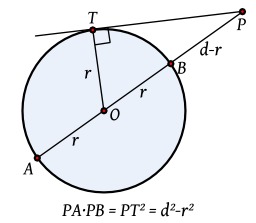
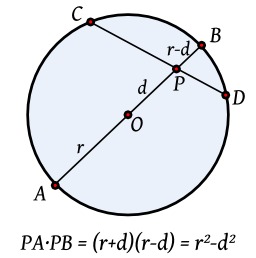
Puissance d'un point intérieur à un cercle
Détermination de la valeur algébrique de la puissance d'un point intérieur à un cercle : PAxPB = (r+d) (r-d).
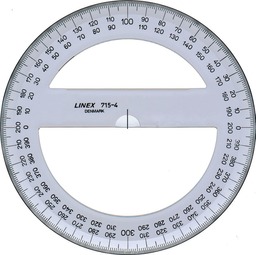
Rapporteur
Un rapporteur (ou rapporteur d'angle) est un outil utilisé en géométrie pour mesurer des angles et pour construire des figures géométriques.
Dessins et plans, Géométrie, Parallèles (géométrie), Thalès, Théorème de, Constructions géométriques, Triangles (géométrie)
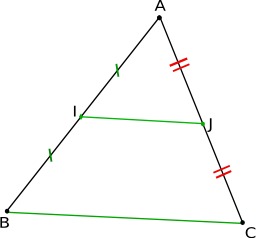
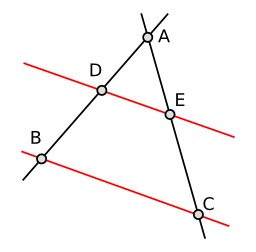
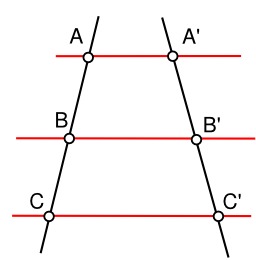
Réciproque du théorème de Thalès
Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès. Si un segment a pour extrémités les milieux de deux côtés d’un triangle, alors il est parallèle au troisième côté, et sa longueur est égale à la moitié de celle de ce troisième côté. Soient I et J les milieux respectifs des segments [AB] et [AC], alors (IJ) // (BC) et IJ = BC ÷ 2.
Segments de Droites
Les différentes représentations d'un segment de droite en géométrie descriptive.
Dessins et plans, Carré, Surfaces (mathématiques) -- Volumes, Géométrie des nombres, Johann Faulhaber (1580-1635), Pyramides (géométrie)
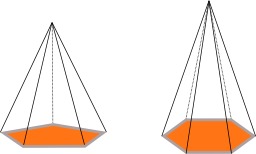
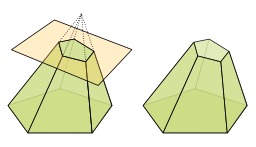
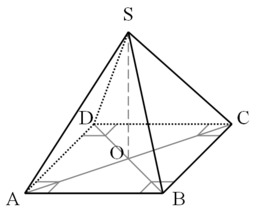
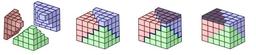
Somme des carrés
Un exemple de preuve sans mots à propos de la somme des premiers carrés : chacune des trois pyramides a pour volume la somme des carrés de 1 à n (n=4 dans cette illustration) ; le parallélépipède final est de côtés n, n+1 et n+1/2. Ce résultat se généralise pour la somme des n premières puissances strictement positives. Cette somme porte le nom de formule de Faulhaber. Johann Faulhaber (1580-1635) est un mathématicien allemand qui collabora avec Kepler.
Photographie, Géométrie, Contribution à la géométrie, Euclide (0323-0285 av. J.-C.), Géométrie euclidienne, Géométrie -- Fondements, Oxford (GB), University of Oxford -- Bibliothèques
Statue d'Euclide
Photographie de la Statue d'Euclide au Musée Universitaire d'Histoire Naturelle à 0xford (Angleterre). En grec ancien Εὐκλείδης Eukleidês (mort à Alexandrie) est un mathématicien de la Grèce antique, auteur des Éléments, qui sont considérés comme l'un des textes fondateurs des mathématiques. La géométrie euclidienne commence avec les Éléments d'Euclide, qui est à la fois une somme des connaissances géométriques de l'époque et une tentative de formalisation mathématique de ces connaissances. Les notions de droite, de plan, de longueur, d'aire y sont exposées et forment le support des cours de géométrie élémentaire. La conception de la géométrie est intimement liée à la vision de l'espace physique ambiant au sens classique du terme.
Dessins et plans, Géodésie, Terre -- Figure, Lithosphère, Pesanteur, Géoïde, Mesure (métrologie), Métrologie
Surfaces de repérage sur la Terre
Croquis des différentes surfaces de repérage sur la Terre. Dans l'acception française du terme, la géodésie s'occupe de la détermination de la forme et des dimensions de la Terre dans son ensemble (autrement dit, de la "figure de la Terre"), ainsi que de son champ de pesanteur (pour l'étude duquel on emploie actuellement le terme de géodésie physique). On définit le géoïde comme étant une surface équipotentielle du champ de pesanteur, choisie arbitrairement, mais très proche du niveau des océans que, par la pensée, nous pouvons prolonger sous les continents. On introduit des systèmes de référence pour décrire le mouvement de la Terre dans l'espace (« système céleste »), ainsi que la géométrie de surface et le champ de pesanteur de la Terre (« système terrestre »). Le choix des meilleurs systèmes de référence, compte tenu des progrès spectaculaires de la métrologie actuelle, est devenu l'une des grandes avancées de la géodésie, la géométrie globale de la Terre étant désormais mesurée à mieux que 1 cm.
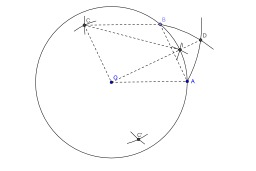
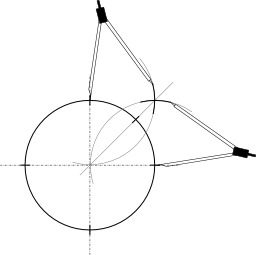
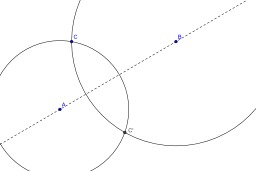
Symétrique d'un point par rapport à une droite
Construction au compas seul du symétrique d'un point par rapport à une droite. Le symétrique du point C par rapport à la droite (AB) est le point d'intersection des cercles de centres A et B et passant par C. Dans la construction la droite (AB) est tracée en pointillés pour permettre de suivre le raisonnement mais elle ne sert pas en tant que telle dans la construction. En géométrie classique plane, le théorème de Mohr Mascheroni, démontré par Georg Mohr en 1672 et par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas seul (sauf le tracé effectif des droites). Est considéré comme constructible tout point d'intersection de deux cercles dont les centres sont des points déjà construits et dont les rayons sont des distances entre des points déjà construits.
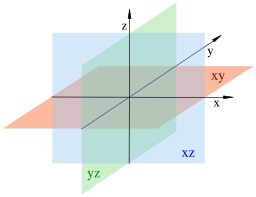
Système de coordonnées dans l'espace
En géométrie analytique, tout point du plan ou de l'espace est « repéré », c'est-à-dire qu'on lui associe un couple (dans le plan) ou un triplet (dans l'espace) de nombres.
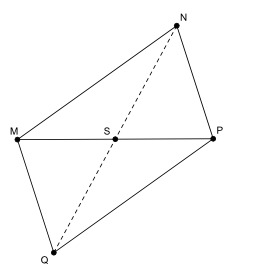
Théorème d'Apollonius
Le théorème de la médiane, ou théorème d'Apollonius, est une relation entre la longueur d'une médiane d'un triangle et la longueur de ses côtés : si S est le centre du parallélogramme, alors 2NS^2 + frac 12 MP^2 = NM^2+NP^2 2NS^2 =frac 12 NM^2+NP^2 NQ^2=NM^2+2NP^2 . Apollonios de Perga ou Apollonius de Perge (en grec ancien Ἀπολλώνιος / Apollốnios, v. 262 – v. 190 av. J.-C.) était un géomètre et astronome grec. Il serait originaire de Pergé (ou Perga, ou encore Pergè actuelle Aksu en Turquie).
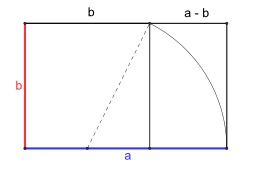
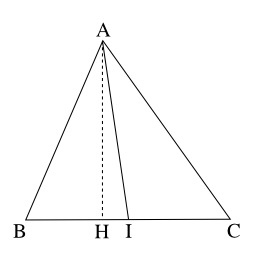
Théorème de la médiane
Médiane et hauteur d'un triangle. Le théorème de la médiane, ou théorème d'Apollonius, est une relation entre la longueur d'une médiane d'un triangle et la longueur de ses côtés. Soit ABC un triangle quelconque, et AI la médiane issue de A. On a alors la relation suivante : AB^2 + AC^2 = 2BI^2 + 2AI^2, Ou encore : AB^2 + AC^2 = {1 over 2} BC^2 + 2AI^2.
Dessins et plans, Géométrie, Pizzas, Aires (surfaces), Aires (surfaces) -- Mesure, Théorèmes -- Démonstration automatique, Théorèmes -- Preuve automatique
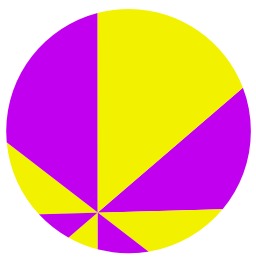
Théorème de la pizza en huit parts
En géométrie euclidienne, le théorème de la pizza donne une égalité ou une inégalité d'aires lors de la partition d'un disque par des droites concourantes. Il porte ce nom en raison d'une forte analogie avec la technique usuelle de découpage d'une pizza. Exemple avec huit parts : aire jaune = aire violette. Source : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_la_pizza.
Dessins et plans, Géométrie, Astronomie, Claude Ptolémée (0100?-0170?), Cercles, Cercles du triangle, Mathématiciens grecs
Théorème de Ptolémée
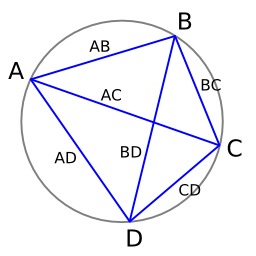
Quadrilatère illustrant le théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne. Il décrit une relation algébrique entre les longueurs des côtés et des diagonales d'un quadrilatère, équivalente à l'inscription du quadrilatère dans un cercle. L'implication directe est attribuée à l'astronome et mathématicien grec Ptolémée, dont il se servit pour ses calculs liés à l'astronomie.
Théorème de Ptolémée
Preuve géométrique du théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne. Il décrit une relation algébrique entre les longueurs des côtés et des diagonales d'un quadrilatère, équivalente à l'inscription du quadrilatère dans un cercle.
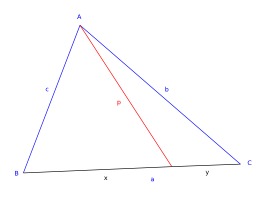
Théorème de Stewart
En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane, due au mathématicien Matthew Stewart dans les années 1746 : Théorème — Soit p une cévienne d'un triangle ABC divisant en X le côté a en deux parties x et y. On a alors la relation suivante : acdot (xy+p^{2}) = xcdot b^{2}+ycdot c^{2}. Matthew Stewart est un mathématicien écossais (1717-1785) reconnu comme un mathématicien important après la publication de son "General Theorems", en 1746.
Théorème de Thalès (cercle)
Théorème de Thalès sur le cercle. Le théorème de Thalès sur le cercle est un théorème de géométrie qui affirme qu'un triangle inscrit dans un cercle et dont un côté est un diamètre est un triangle rectangle.
Théorème de Thalès (cercle)
Théorème de Thalès sur le cercle. Le théorème de Thalès sur le cercle est un théorème de géométrie qui affirme qu'un triangle inscrit dans un cercle et dont un côté est un diamètre est un triangle rectangle.
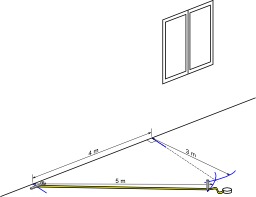
Trace d'une perpendiculaire avec la méthode du 3 4 5
Tracé d'une perpendiculaire en maçonnerie, méthode du 3-4-5 : le triangle est rectangle (théorème de Pythagore).
Dessins et plans, Géométrie, Règles, Dessin -- Matériel, Parallèles (géométrie), Dessin -- Instruments, Dessin -- Technique, Lignes du quadrillage
Tracer une parallèle avec une règle et une équerre
Métode pour tracer une parallèle avec une règle et une équerre. On prend une équerre et l'on appuie un côté sur la droite de référence. On place une règle contre un autre côté de l'équerre. Puis, on appuie fermement sur la règle, et l'on fait glisser l'équerre contre la règle sans appuyer sur l'équerre, ceci afin d'éviter de faire bouger la règle. Source : Mécanique pour l'enseignement technique industriel/Éléments de géométrie (fr.wikiversity.org ).
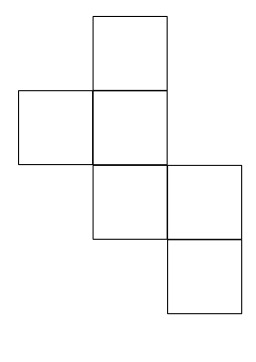
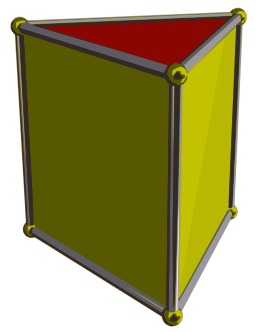
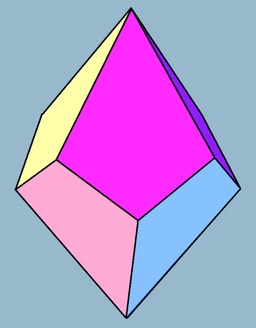
Trapézoèdre tétragonal
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces, par exemple le trapézoèdre tétragonal. Le nom trapézoèdre est trompeur puisque les faces ne sont pas des trapèzes. Le trapézoèdre ou antidiamant ou deltoèdre n-gonal est le polyèdre dual d'un antiprisme n-gonal régulier. Ses 2n faces sont des deltoïdes congrus (ou cerfs-volants). Les faces sont décalées symétriquement.
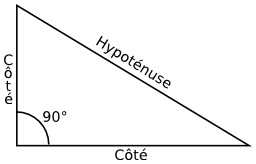
Triangle rectangle
Triangle rectangle : Dans un triangle rectangle, l'hypoténuse (AB) est le côté non adjacent à l'angle droit, ou le côté opposé à l'angle droit (en C).
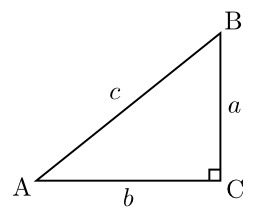
Triangle rectangle
Triangle ABC rectangle en C. Le côté le plus long d'un triangle rectangle est appelé "hypoténuse" (côté AB dans cette image), les deux autres sont les "côtés de l'angle droit". Le théorème de Pythagore énonce, avec les notation du dessin ci-contre, que AB2 = AC2 + BC2.
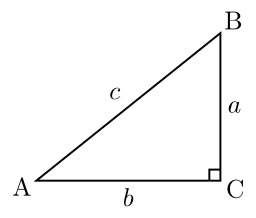
Triangle rectangle
Triangle rectangle en C dont les côtés sont légendés en français : AB = Hypothénuse ; AC = Côté adjacent à l'angle A ; BC = Côté opposé à l'angle A.
Photographie, Géométrie, Vitraux, Métaphore, Triangles (géométrie), Art contemporain, Carlo Roccella (né en 1956), Contribution au vitrail, Art abstrait, Issy-les-Moulineaux (Hauts-de-Seine), Trinité -- Dans l'art
Vitrail moderne à Issy-les-Moulineaux
Vitrail de la Trinité à Issy les Moulineaux, le fils, par Carlo Roccella (né en 1956). Source : http://fr.wikipedia.org/wiki/Carlo_Roccella
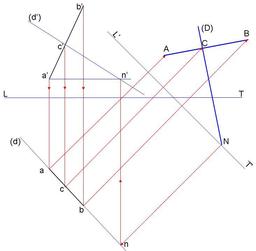
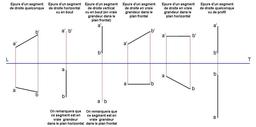
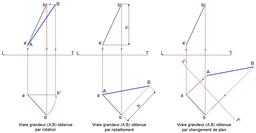
Vraie Grandeur de droite
Vraie grandeur d'une droite obtenue avec la technique dite du changement de plan.
Vtt carbone
Specialized Epic Marathon Carbone 2007, montrant la géométrie générale du cadre, y compris le positionnement spécifique de l'amortisseur arrière. Photo retravaillée par Arnaud Pérat. Le Specialized Epic est un vélo de type VTT destiné à la pratique du X-country, conçu et fabriqué par le constructeur américain Specialized. Il est commercialisé depuis 2003, et a subi une refonte importante en 2009. Comme tous les cadres de bicyclette suspendus de la marque Specialized, l'Epic se base sur une géométrie FSR à point de pivot virtuel, qui permet de limiter l'influence de la transmission sur le travail de la suspension. Cependant, la mise en œuvre de la géométrie diffère selon les générations, surtout au niveau du design de la bicyclette. Source : https://fr.wikipedia.org/wiki/Specialized_Epic