Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.

Votre recherche ...

Nuage de mots clés

rectangles | Dessins et plans | Géométrie | Géométrie affine | Puzzles | Multiplication (arithmétique) | Pavages (mathématiques) | Pentaminos | Photographie | Carré | rectangle | Angles | Parallèles (géométrie) | Parallélogrammes | Polygones | Tablettes d'argile cunéiformes | Pentagones | Diagonales | Racine carrée de deux | Losanges | ...
Les quatre pentaminos. Source : http://data.abuledu.org/URI/50bc18c6-les-quatre-pentaminos

Dessins et plans, rectangles, Puzzles, Multiplication (arithmétique), Pavages (mathématiques), Pentaminos

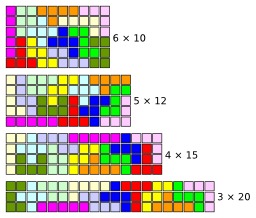
Les quatre pentaminos

Avec les pentaminos, le puzzle classique est de paver une surface rectangulaire sans trou et ni chevauchement. Chaque pentamino, au nombre de 12, contient 5 carrés. En conséquence, le rectangle doit faire 60 carrés de surface ; les dimensions possibles sont donc 6×10, 5×12, 4×15 et 3×20. Les joueurs les plus motivés parviennent à les compléter en quelques heures à la main.

→

Parallélograme. Source : http://data.abuledu.org/URI/51802eaf-pentagone-regulier-et-ses-elements

Photographie, Dessins et plans, Géométrie, Carré, rectangle, rectangles, Angles, Parallèles (géométrie), Parallélogrammes, Polygones, Tablettes d'argile cunéiformes, Pentagones, Diagonales, Racine carrée de deux, Losanges, Quadrilatères, Trapèzes, Aires (surfaces), Aires (surfaces) -- Mesure

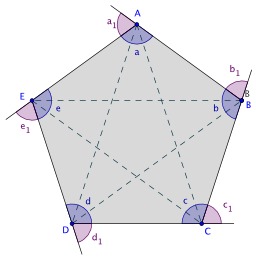
Parallélograme

Exemple de parallélogramme. Un parallélogramme, en géométrie, est un quadrilatère dont les côtés opposés sont parallèles deux à deux

→

Patron de parallélépipède. Source : http://data.abuledu.org/URI/5403243e-patron-de-parallelepipede

Clip art, Géométrie, rectangles, Bricolage -- Appareils et matériel, Ateliers de bricolage (éducation), Découpage (art), Découpages, Pliages en papier, Activités dirigées, Patrons (géométrie)

Patron de parallélépipède

Patron de parallélépipède avec bandes de collage.

→

Rectangle d'or. Source : http://data.abuledu.org/URI/5023eef1-rectangle-d-or

Dessins et plans, Géométrie, rectangles, Géométrie affine, Nombre d'or

Rectangle d'or

Tracé d'un rectangle d'or et divine proportion.

→

Rectangle definition. Source : http://data.abuledu.org/URI/5023ede2-rectangle-definition

Dessins et plans, Géométrie, rectangles, angles droits, Géométrie affine

Rectangle definition

Rectangle avec angles droits symbolisés

→

Rectangles. Source : http://data.abuledu.org/URI/5023ed43-rectangles

Dessins et plans, Infographie couleur, rectangles

Rectangles

Vision artistique de rectangles rouges

→