Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
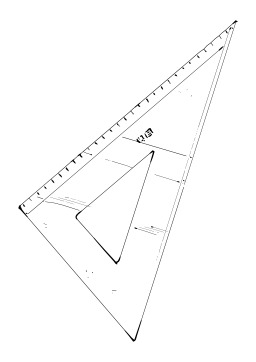
Amplitude (pendule)
Mesure de l'amplitude d'un angle de 90° par un balancier. Le balancier d’une horloge est un élément mobile animé d'un mouvement alternatif de va et vient. Il est horizontal ou circulaire au début et se nomme foliot ou balancier dans les montres actuelles. Il peut aussi prendre la forme d'un pendule, constitué d’une tige verticale, pouvant osciller autour d’un axe horizontal, et comportant un poids à son extrémité basse. Ce poids se présente généralement sous la forme d’un disque bombé, habituellement d’un métal lourd (tel que l’acier), afin de réduire l'influence des forces de résistance de l’air.
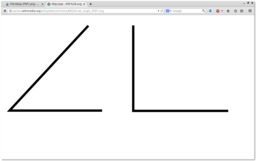
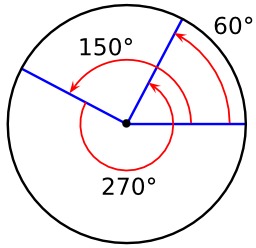
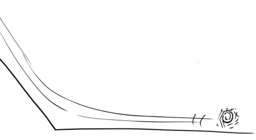
Angle aigu comparé à un angle droit
Angle aigu (à gauche) comparé à un angle droit (à droite), dessin non légendé.
Angle aigu comparé à un angle droit
Angle aigu comparé à un angle droit, traduction en francais als-33.
Dessins et plans, Angles, Liquides, Physique, Gouttes, Vapeurs, Solides, Mouillage (chimie des surfaces), Angle de mouillage
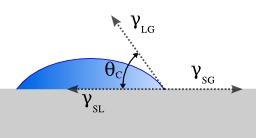
Angle de mouillage entre liquide et solide
Légende : SL = Solide-Liquide, LG = Tension de surface Liquide-Gaz, SG = Solide-Gaz (Vapeur) : l'angle de raccordement d'un liquide sur un solide est l'angle formé par la surface du solide avec la tangente à une goutte du liquide déposée sur ce solide passant par le bord de la goutte. La forme de la goutte est déterminée par la mouillage. L'angle de raccordement n'est pas limité à un solide et un liquide. Ça pourrait être également un interface entre deux liquides ou deux vapeurs. Il est donné par la loi de Young-Dupré.
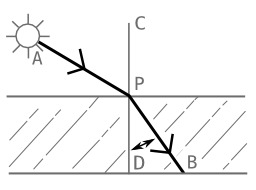
Angle de réfraction
Angle de réfraction : La réfraction, en physique des ondes — notamment en optique, acoustique et sismologie — est un phénomène de déviation d'une onde lorsque sa vitesse change entre deux milieux. La réfraction survient généralement à l'interface entre deux milieux, ou lors d'un changement de densité ou d'impédance du milieu.
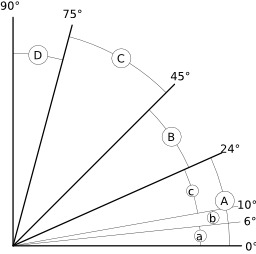
Angles des pentes
Angles des pentes d'escalier : A) rampe ; a) rampe douce, b) rampe normale, c) rampe forte ; B) escalier courant ; C) escalier de machine ; D) échelle.
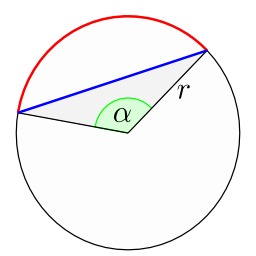
Arc et corde d'un cercle
Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Une corde (en bleu) est un segment de droite dont les extrémités se trouvent sur le cercle. Un arc est une portion de cercle délimitée par deux points (en rouge). Un secteur circulaire est une partie du disque comprise entre deux rayons. Un angle au centre (vert) est un angle formé par deux rayons du cercle.
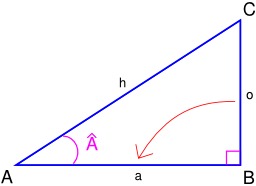
Calcul de la tangente de l'angle A
Représentation géométrique de la tangente dans un triangle rectangle. La tangente d'un angle est le rapport de la longueur du côté opposé à la longueur du côté adjacent :tan(Â) = longueur du côté opposé / longueur du côté adjacent = o/a. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique
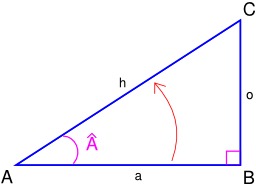
Calcul du Cosinus de l'angle A
Représentation géométrique d'un cosinus dans un triangle rectangle : Le cosinus d'un angle est le rapport de la longueur du côté adjacent par la longueur de l'hypoténuse :cos(Â) = longueur de côté adjacent / longueur de l'hypoténuse = a/h. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique
Calcul du Sinus de l'angle A
Représentation géométrique du sinus dans un triangle rectangle. Le sinus d'un angle est le rapport de la longueur du côté opposé par la longueur de l'hypoténuse :sin(Â) = longueur du côté opposé / longueur de l'hypoténuse = o/h. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
Gravure, Livres, Angles, Walter Crane (1845-1915), Arts décoratifs, Composition (art), Plumes à écrire, Tutoriels, Dessin -- Étude et enseignement
Composition et angles
Walter Crane, Line and Form, page 85 : composition et angles, livres et plume à écrire.
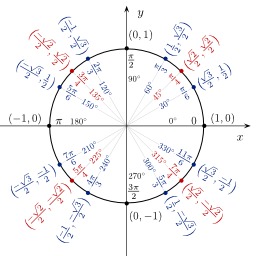
Fonctions trigonométriques dans le cercle unité
Représentation des fonctions trigonométriques dans le cercle unité. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre 0 et π/2. Sur ce cercle sont représentés certains angles communs, et sont indiquées leurs mesures en radians figurant dans l'intervalle [–2π, 2π], soit deux mesures par angle et même trois pour l'angle nul. Notez que les angles positifs sont dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive Ox de l'axe des abscisses coupe le cercle en un point de coordonnées (cos θ, sin θ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
Dessins et plans, Carré, Angles, Humour, Formes (mathématiques), Dessin en noir et blanc, Odysseus, Personnages imaginaires
Hervé le carré a perdu tous ses angles
Hervé le carré a perdu tous ses angles, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Photographie, Dessins et plans, Géométrie, Carré, rectangle, rectangles, Angles, Parallèles (géométrie), Parallélogrammes, Polygones, Tablettes d'argile cunéiformes, Pentagones, Diagonales, Racine carrée de deux, Losanges, Quadrilatères, Trapèzes, Aires (surfaces), Aires (surfaces) -- Mesure
Parallélograme
Exemple de parallélogramme. Un parallélogramme, en géométrie, est un quadrilatère dont les côtés opposés sont parallèles deux à deux
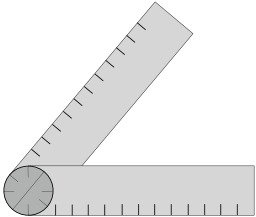
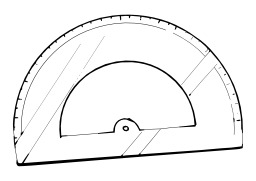
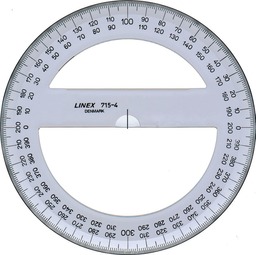
Rapporteur
Un rapporteur (ou rapporteur d'angle) est un outil utilisé en géométrie pour mesurer des angles et pour construire des figures géométriques.
Clip art, Géométrie, Triangle, Angles, Cercle, Philosophes grecs, Philosophes antiques, Thalès, Théorème de
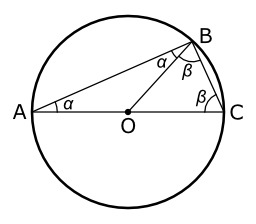
Théorème de Thalès (triangle)
Illustration du théorème de Thalès dans un demi-cercle : propriétés des angles inscrits et complémentaires.
Clip art, Géométrie, Angles, Claude Ptolémée (0100?-0170?), Almageste - Claude Ptolémée (0100?-0170?)
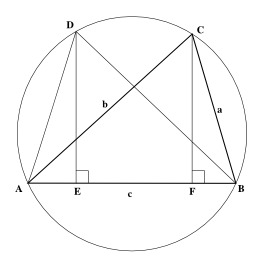
Théorème du cosinus de Ptolémée
Au IIe siècle de notre ère, Ptolémée d’Alexandrie dans son « Almageste », a établi des égalités de rapport équivalentes aux formules d'addition et de soustraction donnant sin(A+B) et cos(A+B). Ptolémée établit une formule équivalente à la formule de l’angle moitié sin^2(A/2)=(1-cos A)/2 et dressa une table de ses résultats.
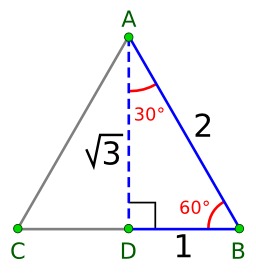
Triangle équilatéral
Représentation géométrique de fonctions trigonométriques : triangle équilatéral divisé en 2 pour calcul du sin, du cos, et de la tan pour 30° et 60°.
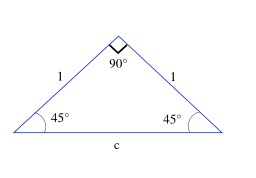
Triangle rectangle isocèle
Triangle rectangle isocèle : c = √2. Pour 45 degrés (π/4 radians) : les deux angles du triangle rectangle sont égaux ; les longueurs a et b étant égales, nous pouvons choisir a = b = 1. On détermine alors le sinus, le cosinus et la tangente d'un angle de 45 degrés en utilisant le théorème de Pythagore : c = sqrt{a^2 + b^2} = sqrt{2}. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.