Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
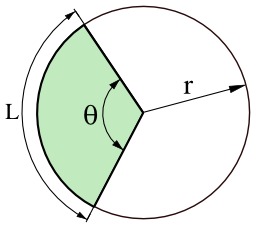
Arc de cercle
Cercle de rayon "r", arc de cercle de longueur "L" soustendu par un angle θ (theta) avec un secteur circulaire de surface "A".
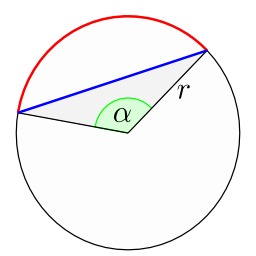
Arc et corde d'un cercle
Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Une corde (en bleu) est un segment de droite dont les extrémités se trouvent sur le cercle. Un arc est une portion de cercle délimitée par deux points (en rouge). Un secteur circulaire est une partie du disque comprise entre deux rayons. Un angle au centre (vert) est un angle formé par deux rayons du cercle.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas, Compas,
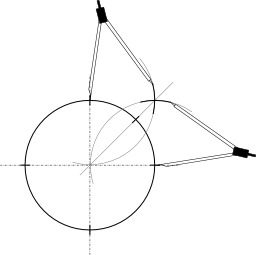
Couper un cercle en 8
Le tracé d'une bissectrice permet de définir deux arcs égaux, et ici de diviser le cercle en 8 parties égales : placer un point entre chaque point déjà placé : on place la pointe du compas sur un des points et l'on trace un arc de cercle à l'extérieur du cercle de base, et l'on fait de même sur le point voisin ; l'intersection des deux arcs définit un point. Puis, on trace à la règle le diamètre passant par ce point-là ; il coupe l'arc de cercle en deux parts égales (bissectrice de l'angle). Ainsi, si le cercle est déjà coupé en 4 parts, on en obtient 8 ; si le cercle est déjà coupé en 12 parts, on en obtient 24. On peut recouper les arcs en 2 par la même méthode, et multiplier ainsi le nombre d'arcs par 2, pour obtenir encore plus d'arcs.
Hercule et les oiseaux du lac Stymphale
Détail de la mosaïque des douze travaux de Liria (Espagne), première moitié du IIIe siècle, représentant Hercule tuant de ses flècles les oiseaux d'acier de Stymphale. (Musée archéologique de Madrid).
La fée Clochette en archer
Dessin d'un elfe-archer habillé en Robin des Bois : rappelle la Fée Clochette de Peter Pan.