Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Cinq Poids en fonte
Cinq poids en fonte hexagonaux pour balance : 5 kg, 2 kg, 1 kg, 0,5 kg, 0,2 kg.
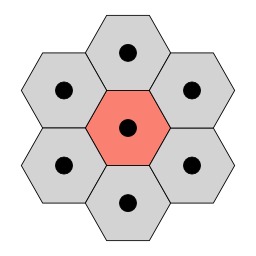
Connectivité hexagonale
Dans le cadre des pavages, la connectivité géométrique indique la relation entre un élément de pavage (une case ou tuile) et ses voisins. On parlera de 6-connectivité lorsqu'une case (ici un hexagone) comporte 6 voisins directs.
Photographie, hiver, Neige, Microscopes, Hexagones, Flocons de neige, Cristallographie, Cristaux de neige, Dendrites (cristallographie)
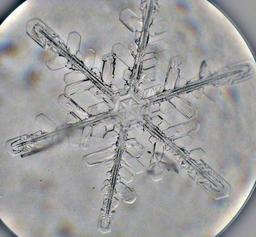
Flocon de neige
Flocon de neige au microscope : dendrites d'un flocon de neige (microscopie optique). Une dendrite est un cristal ramifié, en forme d'arbre (du grec "dendron") : il présente un tronc avec des branches. Les dendrites apparaissent lors de la solidification.
Photographie, hiver, Neige, noir, Vermont (États-Unis), Hexagones, Flocons de neige, Cristallographie, Cristaux de neige, Photographes américains, Velours, Wilson Bentley (1865-1931)
Flocon de neige de Bentley 13
Wilson Bentley (1865-1931), né à Jéricho dans le Vermont aux États-Unis, est le premier photographe connu de flocons de neige. Il perfectionna un procédé où le flocon pouvait être photographié sur du velours noir avant de se fondre ou de se sublimer. Durant sa vie, Bentley réalise plus de 5000 images de cristaux. Il décrit les flocons de neige comme de « petits miracles de beauté » et les cristaux de glace des comme des « fleurs de neige ». Malgré ces descriptions poétiques, Bentley a un œil objectif sur son travail ; son œuvre est à la jonction entre les sciences et l'art.
Photographie, noir, Hexagones, Flocons de neige, Cristallographie, Cristaux de neige, Photographes américains, Velours, Wilson Bentley (1865-1931)
Flocon de neige de Bentley 3
Wilson Bentley (1865-1931), né à Jéricho dans le Vermont aux États-Unis, est le premier photographe connu de flocons de neige. Il perfectionna un procédé où le flocon pouvait être photographié sur du velours noir avant de se fondre ou de se sublimer. Durant sa vie, Bentley réalise plus de 5000 images de cristaux. Il décrit les flocons de neige comme de « petits miracles de beauté » et les cristaux de glace des comme des « fleurs de neige ». Malgré ces descriptions poétiques, Bentley a un œil objectif sur son travail ; son œuvre est à la jonction entre les sciences et l'art.
Photographie, noir, Vermont (États-Unis), Hexagones, Flocons de neige, Cristallographie, Cristaux de neige, Photographes américains, Velours, Wilson Bentley (1865-1931)
Flocon de neige de Bentley 4
Wilson Bentley (1865-1931), né à Jéricho dans le Vermont aux États-Unis, est le premier photographe connu de flocons de neige. Il perfectionna un procédé où le flocon pouvait être photographié sur du velours noir avant de se fondre ou de se sublimer. Durant sa vie, Bentley réalise plus de 5000 images de cristaux. Il décrit les flocons de neige comme de « petits miracles de beauté » et les cristaux de glace des comme des « fleurs de neige ». Malgré ces descriptions poétiques, Bentley a un œil objectif sur son travail ; son œuvre est à la jonction entre les sciences et l'art.
Photographie, hiver, Neige, noir, Vermont (États-Unis), Hexagones, Flocons de neige, Cristallographie, Cristaux de neige, Photographes américains, Velours, Wilson Bentley (1865-1931)
Flocon de neige de Bentley 5
Wilson Bentley (1865-1931), né à Jéricho dans le Vermont aux États-Unis, est le premier photographe connu de flocons de neige. Il perfectionna un procédé où le flocon pouvait être photographié sur du velours noir avant de se fondre ou de se sublimer. Durant sa vie, Bentley réalise plus de 5 000 images de cristaux. Il décrit les flocons de neige comme de « petits miracles de beauté » et les cristaux de glace des comme des « fleurs de neige ». Malgré ces descriptions poétiques, Bentley a un œil objectif sur son travail ; son œuvre est à la jonction entre les sciences et l'art.
Photographie, Neige, noir, Hexagones, Flocons de neige, Cristallographie, Cristaux de neige, Photographes américains, Velours, Wilson Bentley (1865-1931)
Flocon de neige de Bentley 8
Wilson Bentley (1865-1931), né à Jéricho dans le Vermont aux États-Unis, est le premier photographe connu de flocons de neige. Il perfectionna un procédé où le flocon pouvait être photographié sur du velours noir avant de se fondre ou de se sublimer. Durant sa vie, Bentley réalise plus de 5000 images de cristaux. Il décrit les flocons de neige comme de « petits miracles de beauté » et les cristaux de glace des comme des « fleurs de neige ». Malgré ces descriptions poétiques, Bentley a un œil objectif sur son travail ; son œuvre est à la jonction entre les sciences et l'art.
Photographie, hiver, Neige, Microscopes électroniques, Hexagones, Flocons de neige, Cristaux de neige, Dendrites (cristallographie), Cristalographie, Cristaux dendritiques
Flocon de neige hexagonal
Flocon de neige hexagonal (micrographie électronique) présentant des extensions dendritiques.
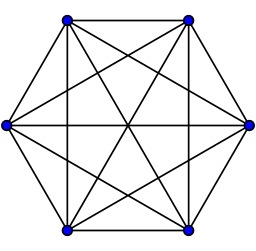
Graphe à six côtés
En théorie des graphes, le graphe complet K_n est l'unique graphe à isomorphisme près possédant n sommets tous reliés deux à deux par une arête, ici 6.
Hexagone magique (3)
Hexagone magique d'ordre 3 : les nombres de 1 à 19 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 38. En mathématiques, un hexagone magique d'ordre n est un arrangement de nombres formant un gabarit hexagonal centré avec n cellules sur chaque côté. La somme des nombres dans chaque rangée ou dans les trois directions font la même somme. Un hexagone magique normal contient tous les entiers allant de 1 à 3n2 − 3n + 1. Il existe seulement deux arrangements respectant ces conditions, celui d'ordre 1 et celui d'ordre 3. De plus, la solution d'ordre 3 est unique.
Hexagone magique (4)
Hexagone magique (4 cases par côté) : les nombres de 3 à 38 sont placés dans cette grille hexagonale pour que la somme des nombres de chaque rangée soit égale à 111.
Hexagone magique (5)
Hexagone magique d'ordre 5 : les nombres de 6 à 66 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 244.
Hexagone magique (7)
Hexagone magique d'ordre 7 : les nombres de 2 à 128 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 635.
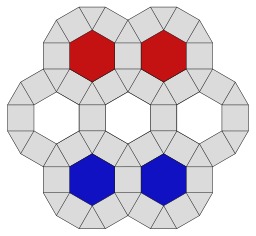
Pavage d'hexagones et de triangles
Pavage régulier à partir de deux formes géométriques, un hexagone (jaune) et un triangle (bleu).
Dessins et plans, Jeux éducatifs, Jeux de logique, Carrés, Triangles, Hexagones, Jeux de stratégie sur plateau, Londres (GB) -- Kensington Palace
Plateau du jeu de Kensington
Kensington est un jeu de société créé par Brian Taylor et Peter Forbes en 1979 et édité par les auteurs. Pour 2 joueurs, à partir de 7 ans pour environ 20 minutes. Le nom du jeu est celui d'un quartier de Londres. Le tablier représente un réseau de triangles, carrés et hexagones ; le jeu comporte 15 pions bleus et 15 rouges. Les règles sont simples et le tablier est séduisant. Malheureusement, le jeu n'est pas très profond. Celui qui forme le premier triangle ou le premier carré est presque assuré de pouvoir disperser les pions adverses et de gagner sans difficulté. Le moyen pour gagner est donc d'être le premier à disperser les pions adverses. La pose et le déplacement des pions font penser au jeu du moulin.
Dessins et plans, Neige, Dix-septième siècle, Savants français, Savants allemands, Johannes Kepler (1571-1630), Hexagones, Symétrie, Symétrie (physique), Cristallographie, Cristaux de neige, Astronomes, René Descartes (1596-1650)
Schémas de cristaux de neige par Descartes
Schémas de cristaux de neige par René Descartes (1596-1650), à partir de l'ouvrage de Johannes Kepler (1571-1630). En 1611, Kepler publie "L’Étrenne ou la neige sexangulaire", premier traité scientifique de 24 pages qui étudie les cristaux de neige, observant notamment leur symétrie hexagonale. René Descartes observe en 1635 à l'œil nu des cristaux de neige et décrit notamment des formes rares, cristaux à douze branches, plaques hexagonales et colonnes.
Photographie, Abeilles mellifères, Géométrie, Miel, Hexagones, Polygones, Agriculture, Produits du rucher, Structures en nids d'abeilles
Structure hexagonale des rayons de miel
Les hexagones réguliers peuvent se juxtaposer les uns les autres sans laisser aucune lacune, comme les carrés et les triangles équilatéraux, et sont ainsi utiles pour construire des pavages. Les cellules des rayons dans une ruche d'abeilles à miel sont hexagonales pour cette raison et parce que cette forme permet une utilisation efficace de l'espace et des matériaux de construction.