Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Connectivité triangulaire
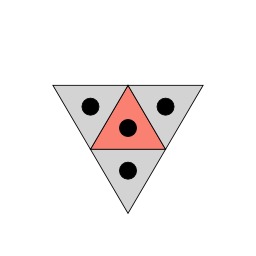
Dans le cadre des pavages, la connectivité géométrique indique la relation entre un élément de pavage (une case ou tuile) et ses voisins. On parlera de 3-connectivité lorsqu'une case comporte 3 voisins directs, comme ici avec le triangle. Les connectivités les plus classiques sont celles correspondant à un pavage régulier :
Deux équerres dos à dos
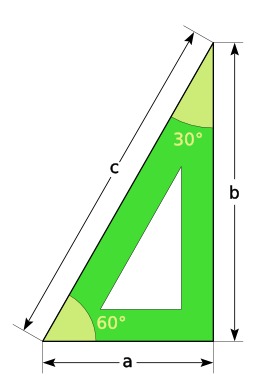
Deux équerres dos à dos, hypothénuse contre hypothénuse, formant un carré.
Pavage d'hexagones et de triangles
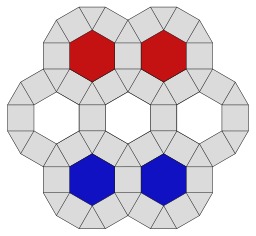
Pavage régulier à partir de deux formes géométriques, un hexagone (jaune) et un triangle (bleu).
Pavage jaune, bleu et vert
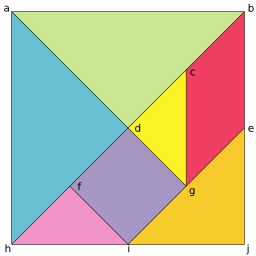
Pavage régulier obtenu avec deux formes géométriques, un carré (jaune) et un triangle (bleu, vert).
Dessins et plans, Jeux éducatifs, Jeux de logique, Carrés, Triangles, Hexagones, Jeux de stratégie sur plateau, Londres (GB) -- Kensington Palace
Plateau du jeu de Kensington
Kensington est un jeu de société créé par Brian Taylor et Peter Forbes en 1979 et édité par les auteurs. Pour 2 joueurs, à partir de 7 ans pour environ 20 minutes. Le nom du jeu est celui d'un quartier de Londres. Le tablier représente un réseau de triangles, carrés et hexagones ; le jeu comporte 15 pions bleus et 15 rouges. Les règles sont simples et le tablier est séduisant. Malheureusement, le jeu n'est pas très profond. Celui qui forme le premier triangle ou le premier carré est presque assuré de pouvoir disperser les pions adverses et de gagner sans difficulté. Le moyen pour gagner est donc d'être le premier à disperser les pions adverses. La pose et le déplacement des pions font penser au jeu du moulin.