Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
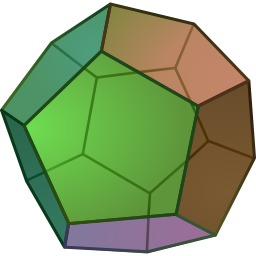
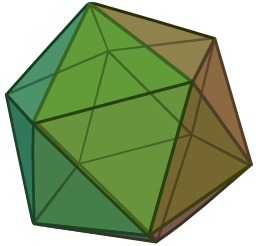
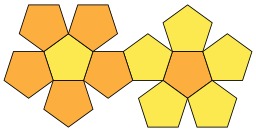
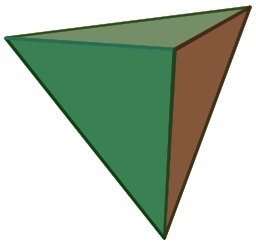
Composé polyédrique de cinq tétraèdres
Composé polyédrique de cinq tétraèdres (Wenninger modèle 25). Un composé polyédrique est un polyèdre qui est lui-même composé de plusieurs autres polyèdres partageant un centre commun, l'analogue tridimensionnel des composés polygonaux tels que l'hexagramme. Enveloppe convexe : Dodécaèdre ; Noyau : Icosaèdre ; Source : http://fr.wikipedia.org/wiki/Compos%C3%A9_poly%C3%A9drique.
Dessins et plans, Géométrie, Cauchy (Augustin Louis, baron), 1789-1857, Dodécaèdres, Polyèdres, Projection stéréographique
Dodécaèdre
Le dodécaèdre, un polyèdre régulier convexe. En 1811, Cauchy (1789-1857) s’intéresse dans son premier mémoire à l’égalité de polyèdres convexes dont les faces sont égales. Il propose une démonstration du théorème de Descartes-Euler, concernant les nombres de sommets, de faces et d'arêtes d'un polyèdre convexe. Sa preuve consiste à projeter le polyèdre en un graphe planaire suivant ce qui est aujourd’hui appelé une projection stéréographique. Cependant, Cauchy commit une erreur, en ne faisant pas d’hypothèse claire sur les polyèdres étudiés. Dans son second mémoire en 1812, il donna des formules pour calculer les angles diédraux.
Photographie, Étoiles, Polyèdres, Formes (mathématiques), Artistes néerlandais, Sculpture, Maurits Cornelis Escher (1898-1972), Arts et sciences
Dodécaèdre étoilé d'Escher
Sculpture du petit dodécaèdre étoilé qui apparait dans Gravitation, 1952, d'après un dessin de M. C. Escher. Devant l'immeuble de "Mesa+" sur le Campus. En géométrie, le petit dodécaèdre étoilé est un solide de Kepler-Poinsot. C'est un des quatre polyèdres réguliers non convexes. Il est composé de 12 faces pentagrammiques, avec cinq pentagrammes se rencontrant à chaque sommet. Les 12 sommets coïncident avec ceux d'un icosaèdre. Les 30 arêtes sont obtenues en reliant chacun des 12 sommets aux 5 sommets les plus éloignés de lui, autres que le sommet diamétralement opposé. Elles sont partagées par le grand icosaèdre. Source : https://fr.wikipedia.org/wiki/Petit_dod%C3%A9ca%C3%A8dre_%C3%A9toil%C3%A9
Dessins et plans, Géométrie, Solides, Tétraèdres, Polyèdres, Groupes de rotations, Symétrie, Symétrie (physique)
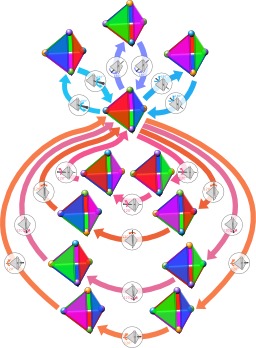
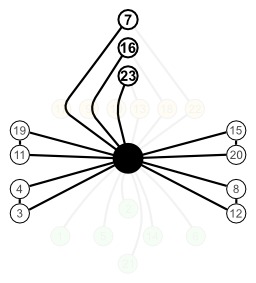
Groupe de symétrie du tétraèdre régulier
Un tétraèdre régulier peut être placé dans 12 positions distinctes par une seule rotation. Celles-ci sont illustrées dans le format d'un graphe de cycles avec des rotations à 180° par rapport à une arête (flèches bleues) et à 120° par rapport à un sommet (flèches rouges) qui permutent le tétraèdre dans toutes les positions. Les 12 rotations forment le groupe (de symétrie) de rotation de la figure.
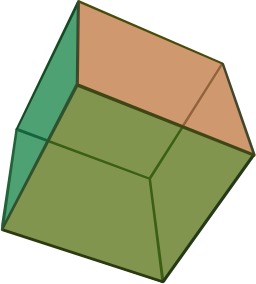
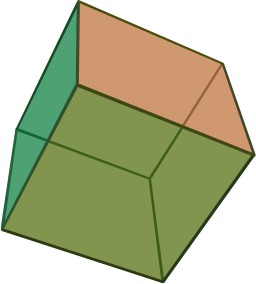
Hexaèdre régulier, le cube
En géométrie des solides, un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube. Le terme hexaèdre vient du grec heksaedros et du bas latin hexahedrum, ce qui justifie la présence de la lettre h dans la traduction anglaise "hexahedron".
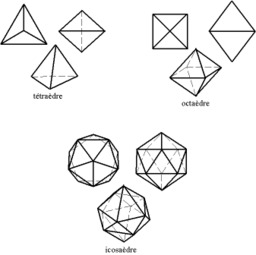
Les trois polyèdres réguliers convexes à faces triangulaires
Plusieurs polyèdres (réguliers ou non) ont des faces triangulaires, comme le tétraèdre, l'octaèdre, l'icosaèdre et le grand icosaèdre. Les polyèdres dont toutes les faces sont des triangles équilatéraux sont appelés deltaèdres.
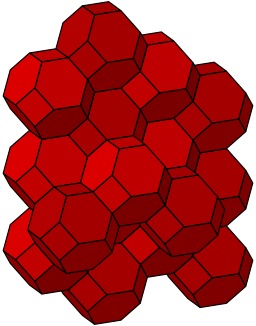
Nids d'abeille partiels
En géométrie, les polyèdres obliques infinis sont une définition étendue des polyèdres, créés par des faces polygonales régulières, et des figures de sommet non planaires. Beaucoup sont directement reliés aux nids d'abeille convexes uniformes, étant la surface polygonale d'un nid d'abeille avec certaines cellules enlevées. En tant que solides, ils sont appelés nids d'abeille partiels et aussi éponges. Ces polyèdres sont aussi appelés pavages hyperboliques parce qu'ils peuvent être regardés comme reliés aux pavages de l'espace hyperbolique qui ont aussi un défaut angulaire négatif.
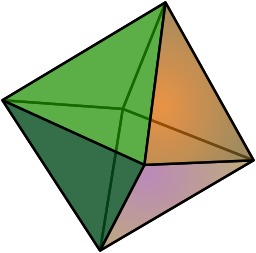
Octaèdre régulier
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces, notamment l'octaèdre régulier. Un octaèdre dont toutes les faces sont triangulaires, possède alors douze arêtes et six sommets.
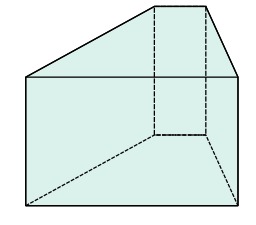
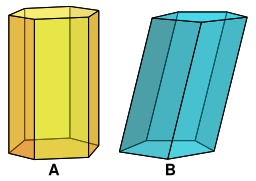
Prisme droit et prisme oblique
Prisme droit (A, jaune) et prisme oblique (B, bleu). Lorsque le plan est perpendiculaire à la droite génératrice (d), le prisme est appelé prisme droit. Lorsque le prisme est droit, les faces latérales sont des rectangles.
Rotations du tétraèdre
Rotations du tétraèdre : Tout groupe de symétrie dont les éléments ont un point fixe commun, ce qui est vrai pour tous les groupes de symétrie de figures bornées, peut être représenté comme un sous-groupe du groupe orthogonal O(n) en choisissant comme origine un point fixe. Le groupe de symétrie propre est alors un sous-groupe du groupe spécial orthogonal SO(n), c'est pourquoi il est aussi appelé le groupe de rotation de la figure.
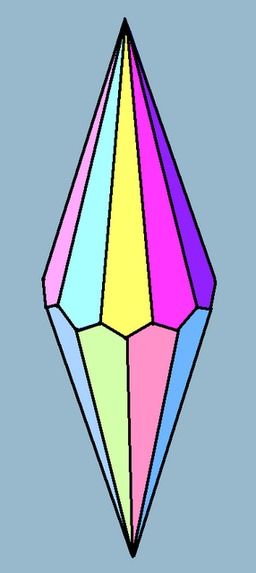
Trapézoèdre hexagonal
Trapézoèdre hexagonal. La partie n-gonale du nom ne fait pas référence aux faces mais à l'arrangement des sommets autour d'un axe de symétrie. L'antiprisme dual n-gonal possède deux faces n-gonales. Un trapézoèdre n-gonal peut être décomposé en deux pyramides n-gonales égales et un antiprisme n-gonal.
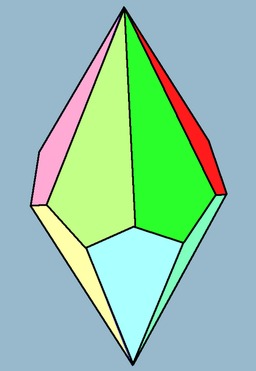
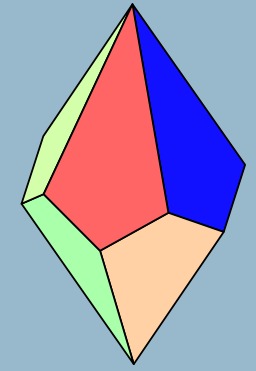
Trapézoèdre pentagonal
Trapézoèdre pentagonal : 10 faces en cerf-volant - dual : antiprisme pentagonal. Le trapézoèdre pentagonal est le premier solide différent des solides de Platon utilisé comme un dé dans les jeux de rôle tels que Donjons et Dragons. Ayant 10 côtés, il peut être utilisé en répétition pour générer n'importe quelle probabilité discrète désirée de base décimale.
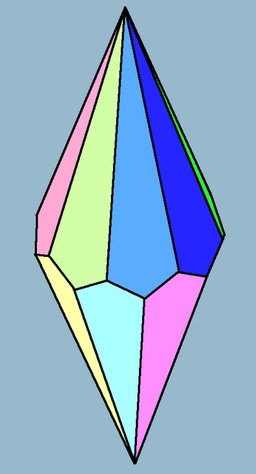
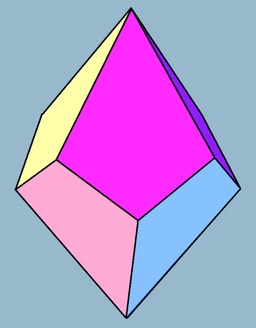
Trapézoèdre tétragonal
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces, par exemple le trapézoèdre tétragonal. Le nom trapézoèdre est trompeur puisque les faces ne sont pas des trapèzes. Le trapézoèdre ou antidiamant ou deltoèdre n-gonal est le polyèdre dual d'un antiprisme n-gonal régulier. Ses 2n faces sont des deltoïdes congrus (ou cerfs-volants). Les faces sont décalées symétriquement.
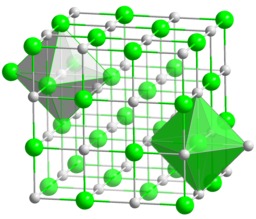
Structure du chlorure de sodium
Structure cristalline cubique à faces centrées du chlorure de sodium (NaCl) : mise en valeur des polyèdres de coordination au sein de la maille. La structure NaCl correspond à deux sous réseaux cubiques à face centrée d'ions, décalés de la moitié du côté de la maille selon l'une des directions des côtés de la maille. La plupart des solides sont des cristaux. Les atomes d'un cristal sont disposés dans l'espace de manière régulière et ordonnée. Les distances interatomiques restent constantes, on parle d'ordre à grande distance
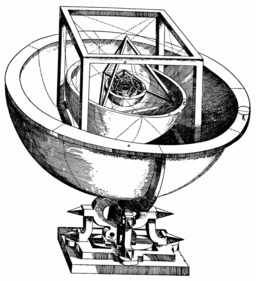
Système solaire de Képler
Source : "Mysterium Cosmographicum" (1596). Le modèle d’Univers de Képler, fondé sur les cinq polyèdres réguliers. La théorie des solides emboîtés, qui amènera plus tard Kepler à découvrir deux nouveaux solides réguliers (voir Les polyèdres de Kepler-Poinsot), si elle nous paraît fantaisiste aujourd’hui, a permis à Kepler d’entrer en contact avec ses contemporains Galilée et Tycho Brahe, mathématicien impérial à la cour de Prague. Ce livre a surtout été apprécié en son temps car il constituait le premier plaidoyer convaincant pour la théorie copernicienne, ne se contentant pas, ainsi que Rheticus l'avait fait, de présenter les avantages du système héliocentrique du point de vue mathématique. Kepler, en effet, cherche (et croit avoir trouvé) les causes (physiques et métaphysiques) du nombre, de la disposition et des mouvements des planètes. Cette recherche des causes (physiques), que Kepler poursuivra tout au long de sa vie, constitue l'acte fondateur de l'invention d'une nouvelle science : l'astrophysique.