Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Objets en déplacement dans l'espace-temps
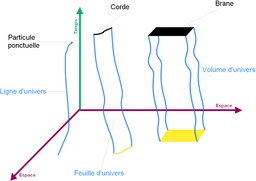
Une ligne d'univers, une feuille d'univers et un volume d'univers, engendrés par une particule ponctuelle, une corde, et une brane. Une ligne d'univers trace la trajectoire d'un seul point dans l'espace-temps, défini comme collection de points appelés événements, avec un système coordonné et continu, identifiant les événements. Chaque événement peut être libellé par quatre nombres : une coordonnée de temps et 3 coordonnés d'espaces ; donc l'espace-temps est un espace quadridimensionnel. Une feuille d'univers est la surface bidimensionnelle analogue, tracée par une ligne (comme une corde) voyageant à travers l'espace-temps. La feuille d'univers d'une corde ouverte est un ruban, et celle d'une corde fermée, un cylindre. Source : http://fr.wikipedia.org/wiki/Ligne_d%27univers
Relativité restreinte : collision entre deux particules
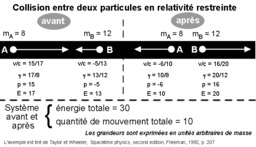
Conservation du quadrivecteur énergie-impulsion dans une collision entre deux particules. Une collision de deux particules est représenté dans la figure ci-contre. Une particule A de masse 8 (en unités arbitraires) animée d'une vitesse v/c de 15/17 dirigée vers la droite frappe une particule de masse 12 arrivant en sens inverse avec une vitesse v/c de 5/13 (les chiffres ont été choisis pour que les calculs "tombent juste"). Après la collision, A rebondit dans l'autre sens en ayant communiqué à B une partie de sa quantité de mouvement. L'énergie totale, somme des énergies des particules A et B est conservée, de même que la quantité de mouvement totale. Les grandeurs E et p indiquées représentent en réalité (E/c2) et (p/c) et sont exprimées en unités de masse, arbitraires. Avec ces grandeurs on a la relation E 2 = p 2 + m 2. Le facteur γ est toujours défini par γ = [1 - (v/c)2]-1/2.
Photographie, Plaques commémoratives, Albert Einstein (1879-1955), Espagnol (langue), Bancs, Relativité (physique), Homme -- Position assise, Montevideo (Uruguay)
Rencontre entre Einstein et Vaz Ferreira à Montevideo
Monument et plaque commémorative de la rencontre entre Einstein et Vaz Ferreira, Montevideo, Uruguay. Physicien. - Membre, Preußische Akademie der Wissenschaften, Berlin (1914-1933). - Professeur, Institute of advanced study, Princeton university, N.J. (1933-1955). - Prix Nobel de physique (1921). Source : data-bnf
Photographie, Dessins et plans, loup, Lièvres, Bateaux, Grenouilles, Antiquités, Gravure, Peinture, Clip art, Balles et ballons, Amphibiens, Fleurs, Géométrie, Couleurs, Accumulateurs, Piles électriques, Plages, Forêts, Sable, Parasols, Cuisine (pain), Jardinage, Jardins, Réfrigérateurs, Réfrigération et appareils frigorifiques, Bains, Bovins de boucherie, Crustacés, Cuisine -- Appareils et matériel, Nuages, Produits viticoles, feu, Linux (système d'exploitation des ordinateurs), Compas, Salades, Livres illustrés pour enfants, Ombres, laine, Poisson, Plantes des jardins, Confitures, Outillage, Pêches, Cartes à jouer, Mer, Architecture végétale des jardins, Légumes, Potages, Navires à voiles, Découpage (cuisine), Viande, Viande -- Coupe, Étoiles, Cuisine (porc), Saucisses, Enseignes, Tables (meubles), Ongle, Cuisine (aliments naturels), Thé, Bleu, Mouton (viande), soleil, Cuisine (oeufs), Peur chez les animaux, Caricatures et dessins humoristiques, noir, Mécanique, Navires, Triangle, Oeufs, Baies (fruits), Porc, Émotions, Albums à colorier, Nombres cardinaux, Éléments de cuisine, Ustensiles de cuisine, Dinde (viande), Nouvelle-Zélande -- Civilisation, Boissons non alcoolisées, Peur, Pâtisseries, Familles, Fêtes -- Accessoires, Cuisine (fromage), Gelées (confiserie), Maillots de bain, Alimentation, Ciel, Temps -- Systèmes et normes, Oeufs -- Coquilles, Poissons d'eau douce, Parents et enfants, Cuisine (poisson), Véhicules prioritaires, Poulet (viande), Râteaux, Animaux des forêts, Cheminées, Couple -- Psychologie, Espace-temps, Cuisine (sucre), Bains de soleil, Terre, Veaux, Vents, Pyramides, Couple, Graines, Filage à la main, Poissons de mer, Rouge, Aluminium, Vert, Sacs, Membres, Cercle, Navires -- Équipement, Physique, Lumière, Lumière -- Propagation, Joie, Géologie -- Cartes, Poisson rouge, Saumon rouge, Agriculture -- Outillage, Coeur, Art médiéval, Trèfles, Pyramides -- Égypte, Cristaux, Blé, Batteries, Marbre, Fillettes, Caricature, Calcaire, Plantes méditerranéennes, Géométrie euclidienne, Navigation à voile, Cuisine (légumes verts), Sacs en tissu, Pelles, Thalès, Théorème de, Seizième siècle, Dix-neuvième siècle, Dix-septième siècle, Cuivre, Grumes, Albums, Pères, Pères et filles, Sentiers, Maisons individuelles, Pattes, Refus d'obéissance, Jardins médiévaux, Lièvre d'Europe, Méditerranée (région), Cuisine (thym), Aliments crus, Parapente, Vol libre, Dix-huitième siècle, France (Révolution) (1789-1799), Albrecht Dürer (1471-1528), Vinaigre, Poisson fumé, Poisson salé, Auckland (Nouvelle-Zélande), Nouvelle-Zélande (1945-....), Aliments, Cuisine (fruits), Aliments d'origine animale, Aliments fermentés, Cuisine (légumes), Produits de l'oeuf, Boissons alcoolisées, Hérodote (0484?-0420? av. J.-C.), Circulation, Vents -- Vitesse, Métamorphisme (géologie), Savants français, Cuisine (aliments crus), Cuisine (fruits de mer), Cuisine (aliments surgelés), Volaille (viande), Cuisine (poulet), Cuisine (volaille), Produits du blé, Sirops, Sauce à salade, Cuisine (viande), Cuisine (plantes odoriférantes), Crèmes (desserts), Entremets, Poisson surgelé, Agneau (viande), Desserts, Hors-d'oeuvre, Cuisine (baies), Cuisine (vinaigre), Ondes, Cuisine (céréales), Jeux de plage, Conduits d'évacuation de fumées, Fumées, Pull-over, Bronzage, Astérides, Seaux, Serviettes, Chlorure de sodium, Cycle hercynien, Boeuf (viande), Rôtis, Rotissoires, Plats complets, Astacidés, Cuisine (écrevisses), Décapodes (crustacés), Écrevisses, Vinaigrette, Champignons cultivés, Cuisine (champignons), Cuisine (truffes), Truffe du Périgord, Tubéracées, Cassis, Cassissier, Cuisine (cassis), Aliments -- Composition, Blanquette, Cuisine (veau), Veau (viande), Veaux -- Alimentation, Omble de fontaine, Poissonneries, Saumons, Saumons -- Pêche commerciale, Cuisine (semoule), Semoule, Cônes de pin, Pignons (graines), Aliments enrichis, Cuisine (restes), Tourtes, Deux, Jeux de société, Trois, Soupes, Infusions, Lumière, Théorie ondulatoire de la, Cuisson sur réchaud de table, Fondues, Savants allemands, Jumeaux, Interférence (optique), Rhubarbe, Augustin Fresnel (1788 - 1827), Diffraction, Ondes -- Diffraction, Énergie, Photons, Temps, Mesure du, France (Chute des Girondins) ( 30 mai-2 juin 1793), Exécutions capitales et exécuteurs, France (1793), Espace de Minkowski, Relativité (physique), Cônes de lumière, Relativité générale (physique), Architecture égyptienne, Constructions en pierres sèches, Cuisine (rhubarbe), Rhubarbes, Cuisine (boeuf), Cuisines, Aliments -- Consommation, Césium, Horloges à césium, Horloges atomiques, Berne (Suisse), Échelles de temps atomique, Temps (droit international), Johannes Kepler (1571-1630), Des révolutions des orbes célestes - Nicolas Copernic (1473-1543), Héliocentrisme, Énergie éolienne en mer, Portance, Aérodynamique, Relativité restreinte (physique), Muons, Rayons cosmiques, Aquarelle, Le lièvre - Albrecht Dürer (1471-1528), Peintres allemands, Cuisine (plantes aromatiques), Résistance à la chaleur, Thymus (plantes), Abats, Cuisine (abats), Tripes, Aliments -- Réfrigération, Entreposage frigorifique, Frigidaire, Frigo, Danse maorie, Ethnologie -- Nouvelle-Zélande, Linux (logiciels), Rugby, Bayonne (Pyrénées-Atlantiques), Ferias, Aliment, Chevreau (viande), Tacuini sanitatis - al-Muẖtār ibn al-Ḥasan ibn ʿAbdūn ibn Saʿdūn Ibn Buṭlān (10..-1066?), Tangram, Corrosion, Corrosion électrochimique, Assemblages à rivets, Corrosion galvanique, Réactions chimiques -- Mécanismes, Électricité, Symétrie, Constructions géométriques, Génie mécanique, Ressorts et suspension, Ressorts, Volutes, Algues marines, Algues -- Aspect économique, Navires -- Australie, Navires -- Déchets -- Élimination, Navires océanographiques, Navires -- Règlements de sécurité, Sargasses, Mer des, Auteurs arabes, Yuwānīs Ibn Buṭlān (10..-1066?), Jardins -- Aspect symbolique, Famille -- Anthropologie, Famille -- Loisirs, Famille -- Santé et hygiène, Mouton (laine), Quenouilles, Regroupement familial, Veillées, Scènes de la vie quotidienne, Vie quotidienne, Révolution industrielle, Projection cinématographique, Signes et symboles, Carreau, Cartes à jouer, Jeux avec, Pique, Trèfle, Chaleur -- Convection, Dissipateurs thermiques (électronique), Électronique, Acides aminés, Protéines