Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Gravure, Chouettes, Caricatures et dessins humoristiques, Inscriptions, Savants, Artistes allemands, Conférences, Joseph Wolf (1820–1899), Congrès et conférences, Embryologie
Caricature de savant
Cours d'embryologie, caricature de savant, 1895, par Joseph Wolf (1820–1899) : Trop de science rend bête.
Textes, Chasseurs, Histoire, Seizième siècle, Électeurs, Savants, Hérauts, Chevaliers et chevalerie, Soldats, Collections de costumes, Soldats -- Pièces d'équipement, Deuil -- Coutumes, Juifs, Martin Luther (1483-1546)
Costumes allemands du début du seizième siècle
Planche 62, Costumes allemands du début du seizième siècle, Costumes of All Nations (Londres, 1882) par Albert Kretschmer, peintre du théâtre de la Cour Royale de Berlin, et Dr. Carl Rohrbach : 1-2, 13-14 patriciens ; 3-4, soldats ; 5, électeur ; 6, Dr Martin Luther ; 7, savant ; 8, pleureur ; 9, juif ; 10, chevalier ; 11, chasseur ; 12, héraut impérial.
Peinture, Peintres français, Nains, Dix-neuvième siècle, Géants, Savants, Philosophes, Caricaturistes, Jonathan Swift (1667-1745), Les voyages de Gulliver - Jonathan Swift (1667-1745), Paul Gavarni (1804-1866)
Gulliver et les philosophes de Brobdingnag
Gulliver et les philosphes (géants) de Brobdingnag par Paul Gavarni, caricature des savants de l'époque.
Photographie, Savants, Hérodote (0484?-0420? av. J.-C.), Histoire de la guerre du Péloponnèse - Thucydide (0460?-0395? av. J.-C.), Histoires - Hérodote (0484?-0420? av. J.-C.), Thucydide (0460?-0395? av. J.-C.)
Hérodote et Thucydide
Hérodote et Thucydide ; source : "Bibliothek des allgemeinen und praktischen Wissens. Bd. 5" (1905), Abriß der Weltliteratur, Seite 46. Hérodote est un savant grec qui parcourt durant sa vie l'Égypte actuelle et le Moyen-Orient, allant jusqu'à Babylone. Dans ses Enquêtes, il veut faire œuvre de mémorialiste et raconte des événements récents, les guerres médiques, « afin que le temps n'abolisse pas les travaux des hommes ». Il se place donc dans une perspective historique qui fait qu'on a pu le qualifier de « père de l'histoire ». Thucydide a posé la méthode historique, dans le sens d'une recherche de « vérité » dans le récit, et non plus simplement de « mémoire ». Dans son Histoire de la guerre du Péloponnèse, il s'attache à relater les causes de la guerre, les faits déclencheurs, puis il raconte chronologiquement cette guerre, restant au plus près des événements, afin de donner un portrait fidèle de ce conflit qu'il considère être fondamental dans l'histoire du monde et qu'il veut expliquer aux générations futures. Il a également une vision profondément rationnelle des faits, ne voyant pas dans l'enchaînement de ceux-ci l'intervention des dieux mais la conséquence des actions des hommes.
Photographie, Savants, Scriptorium, Portraits (photographie), Dictionnaires anglais, James Augustus Henry Murray (1837-1915), Lexicographes
James Murray dans son scriptorium
James Murray dans son scriptorium alimenté par les fiches des contributeurs à l'Oxford English Dictionary : montage Cécédille pour l'intervention sur Wikipédia à l'EPN de Pessac-33. Source : https://commons.wikimedia.org/wiki/File:James-Murray.jpg
Contes, Gravure, Bougies, Ombres, Dix-neuvième siècle, Savants, Nuit, Hans Christian Andersen (1805-1875), Ombres portées
L'ombre d'Andersen - 1
Illustration par Bertall du conte d'Andersen, "L'ombre", 1876 (Hachette, wikisource).
Contes, Gravure, soleil, Dix-neuvième siècle, Savants, Hans Christian Andersen (1805-1875), Ombres portées, Sud
L'ombre d'Andersen -2
Illustration par Bertall du conte d'Andersen, "L'ombre" : "mais, dans les pays chauds, tout repousse bien vite, et, au bout de huit jours, il remarqua, à son grand plaisir, qu’une nouvelle ombre sortait de ses jambes lorsqu’il se promenait au soleil." (wikisource, 1876).
Peinture, Jardins, Balais et brosses, Contes de fées, Garçons, Jardiniers, Savants, Comtesse de Ségur (1799-1874)
Le bon petit Henri, chapitre VII
Le bon petit Henri, chapitre VII, La plante de vie, conte de la Comtesse de Ségur (1799-1874), illustré par Virginia Frances Sterrett (1900–1931) : Henri se souvint heureusement que la fée Bienfaisante lui avait dit d'appeler le docteur qui cultivait le jardin des fées, et il l'appela à haute voix. A peine l'eut-il appelé, qu'il entendit du bruit dans les plantes qui étaient près de lui, et qu'il en vit sortir un petit homme haut comme un balai de cheminée ; il tenait un livre sous le bras, avait des lunettes sur son nez crochu et portait un grand manteau noir de Docteur. "Que cherchez-vous, petit ? dit le Docteur en se redressant. Et comment avez-vous pu parvenir jusqu'ici ?"
Le conte du maître et de son élève
Illustration du conte anglais "Le maître et son élève" de Joseph Jacobs, 1891, par Batten : Le garçon profite de l'absence du savant pour lire une ligne du grimoire secret et fait apparaître Belzébuth.
Photographie, Livres, Nains, Savants, Savants polonais, Wrocław (Pologne), Breslau (Pologne), Figurines de bronze, Intellectuels, Penseurs
Le nain instruit
Le nain instruit (wykształciuch), assis sur deux livres à Wrocław en Pologne : Prof ? Le penseur ?
Peinture, Renaissance, Savants, Masques, Acteurs de théâtre, Allégories -- Dans l'art, Peintres néerlandais, Willem van der Vliet (circa 1584–1642)
Le savant et les acteurs
Le savant (assis à son bureau) et les acteurs et actrices (debout, avec et sans masques), par Willem van der Vliet (circa 1584–1642), peintre hollandais.
Photographie, Oiseaux, Humour, Espagnol (langue), Savants, Lecteurs de livres, Origami, Pliages en papier, Miguel de Unamuno (1864-1936), Produits de bricolage
Oiseau savant en origami
L'oiseau savant lit le livre de Miguel de Unamuno (1864-1936), El sentimiento tragico de la vida.
Gravure, Géométrie, Dix-huitième siècle, Savants, Savants anglais, Perspective cavalière, Axonométrie, Fortifications
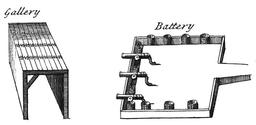
Perspective cavalière en dessins de fortifications
Source : Ephraim Chambers (1680–1740), "Cyclopaedia, or an Universal Dictionary of Arts and Sciences" 1728. La perspective cavalière est une manière de représenter en deux dimensions des objets en volume. Cette représentation ne présente pas de point de fuite : la taille des objets ne diminue pas lorsqu'ils s'éloignent. C'est une forme particulière de perspective axonométrique, où l'on situe les points grâce à leurs coordonnées dans un repère formé de trois axes. Dans cette perspective, deux des axes sont orthogonaux et ont un facteur de report de 1. Le troisième axe est incliné, en général de 30 ou 45° par rapport à l'horizontale, appelé « angle de fuite », et a un facteur de report inférieur à 1, en général. Cette perspective ne prétend pas donner l'illusion de ce qui peut être vu, mais simplement donner une information sur la notion de profondeur. Simple à réaliser, c'est une perspective naïve qui peut traduire un manque de « vision dans l'espace ». Trop souvent utilisée dans les dessins à main levée, elle est malgré tout à déconseiller par son ambiguïté de représentation : un objet éloigné d'un autre peut sembler être plutôt au-dessus ou au-dessous. Cette représentation était utilisée initialement pour la conception des fortifications militaires. Le « cavalier » est un promontoire de terre situé en arrière des fortifications et qui permet de voir par-dessus, et donc de voir les assaillants. La perspective cavalière était donc la vue que l'on avait du haut du cavalier (les anglais utilisent parfois le terme de « high view point », en français « point de vue de haut »). Certains avancent également que c'est la vue qu'a un cavalier du haut de son cheval.
Gravure, Jules Verne (1828-1905), Savants, Fumeurs, Jeunes hommes, Littérature de jeunesse, Édouard Riou (1833-1900)
Portrait d'Axel, le narrateur
Portrait d'Axel le narrateur, illustration par Édouard Riou (1833-1900) de "Voyage au centre de la Terre", 1864, de Jules Verne (1828-1905) : Non, non, répétai-je, non, je ne parlerai pas ! Il voudrait y aller, je le connais ; rien ne saurait l’arrêter. C’est une imagination volcanique, et, pour faire ce que d’autres géologues n’ont point fait, il risquerait sa vie. Je me tairai ; je garderai ce secret dont le hasard m’a rendu maître ! Le découvrir, ce serait tuer le professeur Lidenbrock ! Qu’il le devine, s’il le peut. Je ne veux pas me reprocher un jour de l’avoir conduit à sa perte ! Ceci résolu, je me croisai les bras, et j’attendis. Mais j’avais compté sans un incident qui se produisit à quelques heures de là.
Photographie, Statues, Belgique, Albert Einstein (1879-1955), Bancs, Savants, Homme -- Position assise, Année 1933, Victimes du nazisme
Statue d'Einstein en Belgique
Albert Einstein séjourne durant six mois à De Haan (Belgique) en 1933. Johnny Werbrouck crée une statue de bronze en 2006. Après un séjour aux États-Unis en tant que professeur invité, le physicien prix Nobel Albert Einstein débarqua à Anvers en mars 1933. Comme le NSDAP, le parti d'Adolf Hitler, venait de remporter les élections ce même mois, Einstein et sa femme décidèrent de ne pas rentrer en Allemagne et s'installèrent au Coq dans la partie gauche de la double villa Savoyarde, située au n° 5 de l'avenue Shakespeare. Plus tard, ses belles-filles Ilse et Margot, son assistant Walther Mayer et sa secrétaire Helen Dukas vinrent vivre avec eux. Einstein y recevra la visite de nombreux diplomates, politiciens, savants et artistes dont le peintre James Ensor avec lequel il se liera d'amitié. Sa tête ayant été mise à prix par les nazis et estimant donc la situation trop dangereuse, Einstein quitte Le Coq incognito pour l'Angleterre le 9 septembre 1933 avant de s'installer définitivement aux États-Unis en octobre de la même année. Source: http://fr.wikipedia.org/wiki/Le_Coq
Textes, Lunettes, Paris (France), Mouchoirs, Dix-neuvième siècle, Savants, Serviteurs, Honoré de Balzac (1799-1850), Romanciers français
Une rue de Paris et son habitant - 3
Une rue de Paris et son habitant, 1848, par Honoré de Balzac (1799-1850), chapitre 3 : Madame Adolphe. (490 mots)