Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
Puissance d'un point
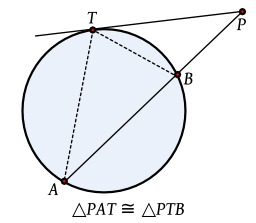
En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
Puissance d'un point
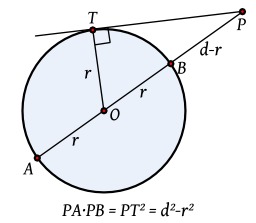
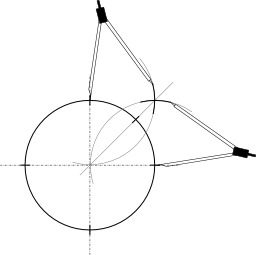
Détermination de la valeur algébrique de la puissance d'un point extérieur à un cercle. En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
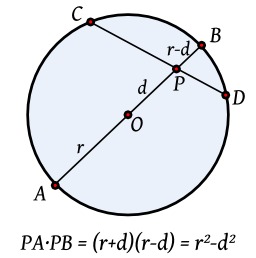
Puissance d'un point intérieur à un cercle
Détermination de la valeur algébrique de la puissance d'un point intérieur à un cercle : PAxPB = (r+d) (r-d).
Dessins et plans, Géométrie, Barcelone (Espagne), Astronomes, Dunkerque (Nord), Trigonométrie, Jean-Baptiste Delambre (1749-1822), Pierre Méchain (1744-1804), Télémètres
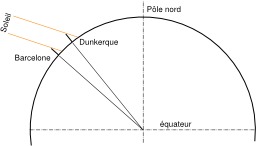
Angle Dunkerque Barcelone
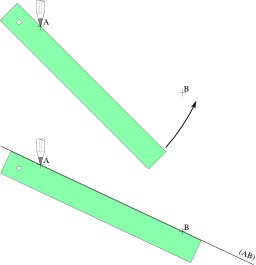
Mesure de l'angle de l'arc de méridien entre Dunkerque (France) et Barcelone (Espagne) en utilisant l'ombre d'un bâton planté à la verticale. Ceci fut fait par des expéditions menées par Delambre et Méchain. Pour mesurer la distance de Dunkerque à Barcelone (qui sont sur un même méridien), on mesura la distance de proche en proche entre des points bien visibles : sommet des églises et des collines. Pour cela, on se place en un point, et on vise l'autre point, selon un principe similaire au télémètre ; la mesure des angles permet de déterminer la distance.
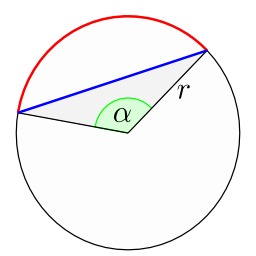
Arc et corde d'un cercle
Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Une corde (en bleu) est un segment de droite dont les extrémités se trouvent sur le cercle. Un arc est une portion de cercle délimitée par deux points (en rouge). Un secteur circulaire est une partie du disque comprise entre deux rayons. Un angle au centre (vert) est un angle formé par deux rayons du cercle.
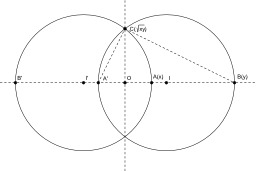
Calcul de racine carrée au compas
Construction au compas seul de la racine carrée du produit xy. Si A a pour abscisse x et B pour abscisse y, on construit les points A' et B' d'abscisses -x et -y Les cercles de diamètres [AB'] et [A'B] se coupent sur l'axe des ordonnées en un point d'ordonnée sqrt{xy} (propriété de la hauteur dans un triangle rectangle). Il est toujours possible de rabattre sqrt{xy} en abscisse par symétrie par rapport à la première bissectrice (constructible au compas).
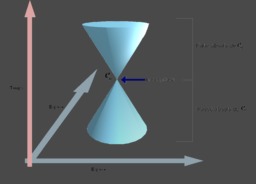
Cône de Lumière
Le cône de lumière de l'évènement e0. La flèche rose montre la dimension temporelle et les flèches grises, les dimensions spatiales. Un événement étant donné, l'ensemble des événements physiquement joignables dans le futur et de ceux du passé à partir desquels on pouvait joindre l'événement donné, forme un cône dans l'espace de Minkowski, appelé cône de lumière, et permettant des raisonnements purement géométriques par des dessins appelés diagrammes de Minkowski. Cet espace est pseudo-euclidien : bien que la métrique ne soit qu'une pseudo-métrique, les géodésiques y sont les droites, ce qui fait dire que cet espace est plat comme dans un espace euclidien. Les inégalités triangulaires qui y sont valables montrent qu'un segment est le chemin le plus long entre deux points, ce qui est une nette différence avec la géométrie euclidienne.
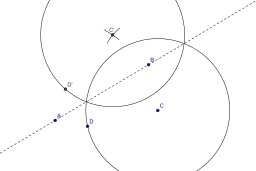
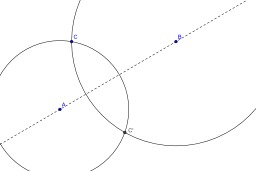
Construction au compas de l'intersection d'une droite et d'un cercle
Construction au compas seul de l'intersection d'une droite et d'un cercle (cas général) : Si la droite (AB) n'est pas un diamètre du cercle, il suffit de construire le symétrique du cercle par rapport à la droite (AB). Les points d'intersection des deux cercles sont aussi les points d'intersection du cercle de départ avec la droite (AB).
Construction d'un parallélogramme au compas
Construction au compas seul du quatrième point d'un parallélogramme : Les points A, B et C étant donnés, le quatrième point D du parallélogramme ABCD est le point d'intersection du cercle de centre A et de rayon BC et du cercle de centre C et de rayon BA non situé dans le demi-plan de frontière (CA) contenant B.
Construction d'un point symétrique par pliage
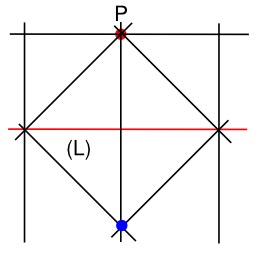
Construction du symétrique d'un point par rapport à une droite par origami : On construit la perpendiculaire à (L) passant par P puis la perpendiculaire à cette perpendiculaire passant par P (autrement dit, la parallèle à (L) passant par P). On construit les deux bissectrices en P à la parallèle à (L) et la perpendiculaire à (L). Ces deux bissectrices vont couper (L) en deux points d'où l'on trace deux nouvelles perpendiculaires à (L). Deux dernières bissectrices vont se couper en le symétrique à P cherché.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
Cordes de Motzkin entre cinq points sur un cercle
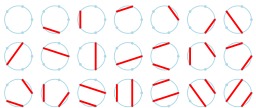
Vingt-une cordes de Motzkin (qui ne se coupent pas) entre cinq points sur un cercle.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
Cordes de Motzkin entre quatre points sur un cercle
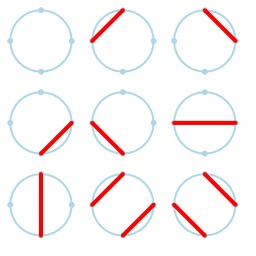
Cordes de Motzkin sur un cercle : les neuf manières de dessiner des cordes qui ne se coupent pas entre quatre points d'un cercle. Le nombre de Motzkin est le nombre de façons de choisir des cordes ne se coupant pas, parmi les cordes reliant n points disposés sur un cercle. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas, Compas,
Couper un cercle en 8
Le tracé d'une bissectrice permet de définir deux arcs égaux, et ici de diviser le cercle en 8 parties égales : placer un point entre chaque point déjà placé : on place la pointe du compas sur un des points et l'on trace un arc de cercle à l'extérieur du cercle de base, et l'on fait de même sur le point voisin ; l'intersection des deux arcs définit un point. Puis, on trace à la règle le diamètre passant par ce point-là ; il coupe l'arc de cercle en deux parts égales (bissectrice de l'angle). Ainsi, si le cercle est déjà coupé en 4 parts, on en obtient 8 ; si le cercle est déjà coupé en 12 parts, on en obtient 24. On peut recouper les arcs en 2 par la même méthode, et multiplier ainsi le nombre d'arcs par 2, pour obtenir encore plus d'arcs.
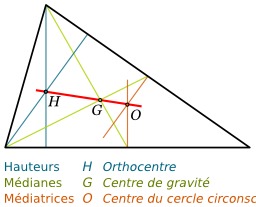
Droite d'Euler
En géométrie euclidienne, dans un triangle non équilatéral, l'orthocentre H, le centre de gravité ou isobarycentre G et le centre du cercle circonscrit \Omega sont alignés et ne sont pas confondus. On appelle droite d'Euler la droite passant par ces trois points. Traduction en français Christophe Catarina.
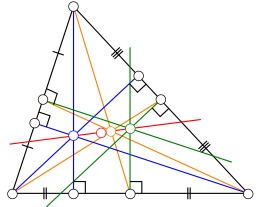
Droite d'Euler dans un triangle
En bleu : les hauteurs ; en orange : les médianes ; en vert : les médiatrices ; en rouge : la droite d'Euler. En géométrie euclidienne, dans un triangle non équilatéral, l'orthocentre H, le centre de gravité ou isobarycentre G et le centre du cercle circonscrit Omega sont alignés et ne sont pas confondus. On appelle droite d'Euler la droite passant par ces trois points.
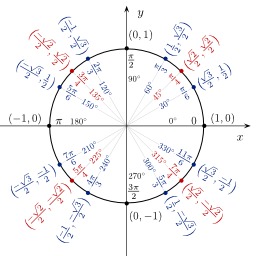
Fonctions trigonométriques dans le cercle unité
Représentation des fonctions trigonométriques dans le cercle unité. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre 0 et π/2. Sur ce cercle sont représentés certains angles communs, et sont indiquées leurs mesures en radians figurant dans l'intervalle [–2π, 2π], soit deux mesures par angle et même trois pour l'angle nul. Notez que les angles positifs sont dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive Ox de l'axe des abscisses coupe le cercle en un point de coordonnées (cos θ, sin θ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
Clip art, Signalisation routière, Panneaux à message variable, Traitement d'images -- Techniques numériques, Traitement vectoriel
Image vectorielle d'Hopital
L'informatique utilise le terme de vecteur, à la fois pour des raisons géométriques et algébriques. Le codage d'une image sur un écran d'ordinateur utilise au choix deux techniques : matricielle et vectorielle. La première utilise des éléments graphiques définis point par point. À chaque pixel est associé la quantité de couleurs primaires correspondante. Si cette méthode est économique en termes de puissance de calcul, un agrandissement de la taille de l'image possède pour conséquence un effet d'escalier. Un dessin vectoriel est une représentation composée d'objets géométriques (lignes, points, polygones, courbes…) ayant des attributs de forme, de position, de couleur, etc. À la différence de la technique précédente, il s'agit d'une méthode plus coûteuse en termes de puissance de calcul mais dans laquelle l'effet d'escalier n'existe pas. La représentation des données en informatique, pour les fonctions de mémoire ou de calcul, se fonde sur des tableaux d'octets. Si un octet est identifié à un scalaire, ce qui se conçoit car deux octets s'additionnent et se multiplient, alors un tel tableau s'apparente à une famille de composantes vectorielles. Pour cette raison, un tel tableau est appelé vecteur. Par extension, le terme de vecteur désigne aussi des tableaux dont les composantes sont autre chose que des nombres, par exemple des pointeurs ou des structures informatiques quelconques.
Intersection d'une droite et d'un cercle au compas
Construction au compas seul de l'intersection d'un cercle avec son diamètre : Si la droite (AB) est un diamètre du cercle, et si le point D n'est pas situé sur (AB). On construit de symétrique de D par rapport à (AB). Les deux points à chercher sont les milieux des deux arcs d'extrémités DD'.
Perspective cavalière à 90°
Comparaison entre les projections orthogonales sur les plans contenant les axes (géométrie descriptive) et la perspective cavalière : report des coordonnées. Pour effectuer une représentation en perspective cavalière, il faut choisir différents paramètres : 1) un plan frontal : un segment contenu dans ce plan, ou dans un plan parallèle, est représenté en vraie grandeur ; 2) un angle de fuite : les perpendiculaires au plan frontal, appelées fuyantes sont représentées dans cette direction ; 3) un coefficient de réduction : les longueurs représentées dans la direction de fuite sont multipliées par ce coefficient de réduction. De plus, l'alignement des points, le parallélisme des droites le rapport des longueurs de deux segments parallèles, et donc les milieux, sont conservés. En revanche, les longueurs, les aires, et les angles ne sont pas conservés dans les plans non frontaux. Les éléments cachés par les faces supposées opaques sont représentés en pointillés; les éléments visibles par l'observateur sont représentés en traits pleins.
Gravure, Géométrie, Dix-huitième siècle, Savants, Savants anglais, Perspective cavalière, Axonométrie, Fortifications
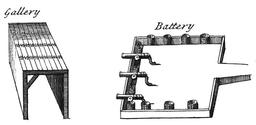
Perspective cavalière en dessins de fortifications
Source : Ephraim Chambers (1680–1740), "Cyclopaedia, or an Universal Dictionary of Arts and Sciences" 1728. La perspective cavalière est une manière de représenter en deux dimensions des objets en volume. Cette représentation ne présente pas de point de fuite : la taille des objets ne diminue pas lorsqu'ils s'éloignent. C'est une forme particulière de perspective axonométrique, où l'on situe les points grâce à leurs coordonnées dans un repère formé de trois axes. Dans cette perspective, deux des axes sont orthogonaux et ont un facteur de report de 1. Le troisième axe est incliné, en général de 30 ou 45° par rapport à l'horizontale, appelé « angle de fuite », et a un facteur de report inférieur à 1, en général. Cette perspective ne prétend pas donner l'illusion de ce qui peut être vu, mais simplement donner une information sur la notion de profondeur. Simple à réaliser, c'est une perspective naïve qui peut traduire un manque de « vision dans l'espace ». Trop souvent utilisée dans les dessins à main levée, elle est malgré tout à déconseiller par son ambiguïté de représentation : un objet éloigné d'un autre peut sembler être plutôt au-dessus ou au-dessous. Cette représentation était utilisée initialement pour la conception des fortifications militaires. Le « cavalier » est un promontoire de terre situé en arrière des fortifications et qui permet de voir par-dessus, et donc de voir les assaillants. La perspective cavalière était donc la vue que l'on avait du haut du cavalier (les anglais utilisent parfois le terme de « high view point », en français « point de vue de haut »). Certains avancent également que c'est la vue qu'a un cavalier du haut de son cheval.
Dessins et plans, Rues, Perspective, Architecture -- Dessins et plans, Dessin d'architecture, Dessin de bâtiment, Dessin en couleurs, Vues d'optique
Perspective et point de fuite
Dans le cadre de la représentation de la réalité en perspective conique, un point de fuite est un point imaginaire destiné à aider le dessinateur à construire son œuvre en perspective. La dénomination point de fuite est celle utilisée en dessin. Les géomètres, dans le cadre de la conception projective de l'espace dégagée à partir des propriétés des représentations en perspectives coniques, les appellent points à l'infini. À chaque direction de l'espace est associé un point de fuite.
Photographie, Géométrie, Carré, Triangle, Urbanisme, Isostasie, Égouts, Plaques de regard, Structures hyperstatiques
Plaque d'égout isostatique
Plaque d'égout isostatique : une plaque d'égout classique n'est jamais parfaitement plane ni l'appui sur lequel elle repose. Il en résulte un bruit de basculement, métal sur métal, chaque fois qu'on marche dessus ou, plus énervant encore, lorsqu'une roue de voiture la traverse. La solution a consisté à supprimer cet appui hyperstatique et à le remplacer par un appui en trois points : deux demi-plaques triangulaires jumelles dessinent un carré coupé en diagonale. Ces demi-plaques sont articulées selon deux côtés opposés du carré, le troisième appui étant constitué par la pointe que l'on relève pour accéder au regard. Source : http://fr.wikipedia.org/wiki/Plaque_d%27%C3%A9gout
Quarante-et-un points violets en cercles
Quarante-et-un points violets en trois cercles concentriques autour d'un point central : petit cercle de huit points et deux grands cercles de seize points.
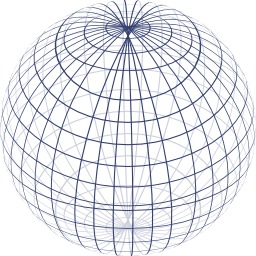
Sphère dans un espace euclidien
En géométrie dans l'espace, une sphère est une surface constituée de tous les points situés à une même distance d'un point appelé centre. La valeur de cette distance au centre est appelée le rayon de la sphère. La géométrie sphérique est la science qui étudie les propriétés des sphères.
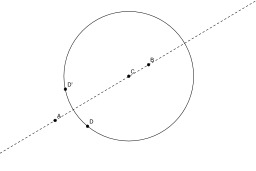
Symétrique d'un point par rapport à une droite
Construction au compas seul du symétrique d'un point par rapport à une droite. Le symétrique du point C par rapport à la droite (AB) est le point d'intersection des cercles de centres A et B et passant par C. Dans la construction la droite (AB) est tracée en pointillés pour permettre de suivre le raisonnement mais elle ne sert pas en tant que telle dans la construction. En géométrie classique plane, le théorème de Mohr Mascheroni, démontré par Georg Mohr en 1672 et par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas seul (sauf le tracé effectif des droites). Est considéré comme constructible tout point d'intersection de deux cercles dont les centres sont des points déjà construits et dont les rayons sont des distances entre des points déjà construits.
Dessins et plans, Géométrie, Règles, Dessin -- Matériel, Dessin -- Instruments, Ligne (art), Dessin -- Technique, Lignes du quadrillage, Points (mathématiques), Ensembles de
Tracer une droite entre deux points avec une règle
Comment prendre en compte la largeur de la mine pour tracer un trait entre deux points : 1) placer le crayon sur un des points A ; s'en servir comme pivot pour la règle vers le point B. 2) tracer un trait passant par ces deux point avec la règle.
Dessins et plans, Physique, Mathématiques -- Notation, Opérations (mathématiques), Règles de somme (physique), Sommes (mathématiques), Vecteurs
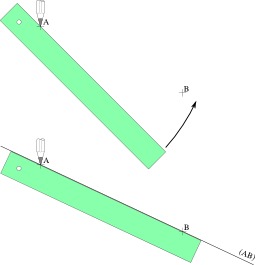
Vecteurs somme
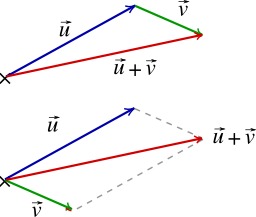
Deux vecteurs overrightarrow{u} et overrightarrow{v} et le vecteur somme. Un vecteur est représenté par un segment orienté (une flèche) ayant pour extrémités un point de départ et un point d'arrivée. L’emplacement dans le plan ou l'espace n’a pas d’importance, deux déplacements de deux points d'origine distincts peuvent correspondre au même vecteur, seuls comptent sa longueur, sa direction et son sens. Il est donc possible de le faire glisser librement dans le plan, parallèlement à lui-même. Des constructions géométriques permettent la définition de l'addition et de la multiplication par un scalaire. Le nom donné aux opérations est la conséquence de la similarité avec les opérations sur les nombres (commutativité, associativité et distributivité, présence d'un élément neutre et absorbant). Pour cette raison, non seulement les noms des opérations mais les notations sont similaires.