Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Mandala de Vajradhatu
Mandala de Vajradhatu (boudhisme tibétain) du XIXème siècle : forme de base carrée avec quatre portes d'entrée, contenant un cercle et un centre (symétrie centrale).
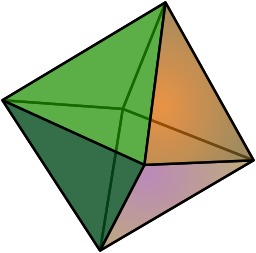
Octaèdre régulier
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces, notamment l'octaèdre régulier. Un octaèdre dont toutes les faces sont triangulaires, possède alors douze arêtes et six sommets.
Dessins et plans, Anatomie humaine, Biologie humaine, Terminologie, Vocabulaire fondamental, Références en biologie clinique, Références professionnelles
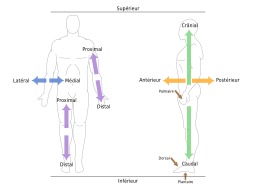
Orientations en anatomie humaine
Qualificatifs d'orientation du Système de référence en anatomie humaine : Crânial ou céphalique = en direction de la tête ou tout simplement supérieur. En embryologie, on utilise aussi l'adjectif « rostral » pour qualifier les futures structures antérieures de l'encéphale. Caudal ou inférieur = vers les pieds (historiquement la nomenclature anatomique servait aussi à décrire l'anatomie des animaux à quatre pattes, donc ce qualificatif désignait la direction de la queue, par opposition au museau ou au bec ou rostre) ; chez l'Homme le coccyx constitue le vestige de cet appendice et reste donc la référence pour le terme « caudal » ; on ne pourra donc pas appliquer cet adjectif aux éléments du membre pelvien (et par extension du membre thoracique) pour lesquels on préfèrera distal et proximal). Médian = situé sur le plan médian du corps (plan de symétrie) ou dans l'axe longitudinal d'un membre. Médial = qui se rapproche du plan médian (positionné en dedans). Latéral = qui s'éloigne du plan médian (positionné en dehors). Antérieur ou ventral = qui regarde / est situé vers l'avant. Postérieur ou dorsal = qui regarde / est situé vers l'arrière. « Dorsal » désigne aussi la face arrière de la main et la face supérieure du pied. Palmaire = pour la face avant de la main, du côté de la paume. Plantaire = pour la face inférieure du pied, du côté de la plante. Proximal = proche de la racine d'un membre. Distal = proche de l'extrémité d'un membre. Source : http://fr.wikipedia.org/wiki/Syst%C3%A8me_de_r%C3%A9f%C3%A9rence_en_anatomie.
Dessins et plans, Géométrie, Jeux mathématiques, Pavages (mathématiques), Mathématiciens, Tuiles, Divertissements mathématiques
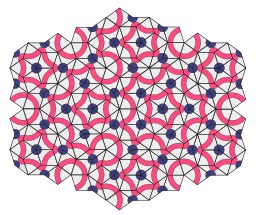
Pavage de Penrose avec tuiles apériodiques
Pavage de Penrose réalisé avec deux tuiles apériodiques. Roger Penrose est un mathématicien anglais. Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement. Plus généralement toute portion finie du pavage, aussi grande soit-elle, se répète infiniment dans le pavage. Les pavages de Penrose ne seraient restés qu'un joli divertissement mathématique si n'avaient été découverts, en 1984, des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux. Les pavages non périodiques, en particulier ceux de Penrose, s'avérèrent alors un modèle plausible de ces étranges matériaux. Cette découverte illustra à nouveau ce que Roger Penrose lui-même avait déjà remarqué en 1973, à propos d’un sujet de relativité générale : « On ne sait jamais vraiment quand on perd son temps ». Source : http://fr.wikipedia.org/wiki/Pavage_de_Penrose.
Peinture, Céphalopodes, Biologie marine, Art nouveau (décoration), Symétrie (art), Pieuvres, Ernst Haeckel (1834-1919), Symétrie (biologie)
Pieuvre
Pieuvre (Pinnoctopus cordiformis) : Planche 54 de "Formes artistiques de la Nature" (Kunstformen der Natur), 1904, livre de lithographies illustratives de sciences naturelles publié par le biologiste allemand Ernst Haeckel (1834-1919) dont les représentations eurent une influence décisive sur le courant de l'Art nouveau au début du XXe siècle, et notamment l'École de Nancy. Cinq céphalopodes "Gamochonia, Trichterkraken".
Photographie, Anglais (langue), Plaques commémoratives, Monuments historiques, Français (langue), Lieux historiques, Nouvelle-France -- Histoire, Québec (Canada) -- Quartier Vieux-Québec, Québec (ville), Sites historiques
Plaque commémorative du Château Frontenac à Québec
Plaque commémorative bilingue du Château Frontenac à Québec : Construit en sept étapes à partir de 1892-93, cet édifice offre un excellent exemple des hôtels de style Château établis par les compagnies ferroviaires du Canada. Rehaussé par la splendeur du site, il évoque le romantisme des châteaux de la Loire des XIV° et XV° siècles. Bruce Price, qui en a conçu le plan, a toutefois délaissé la symétrie classique de ces modèles au profit de l'éclectisme pittoresque en vogue à la fin du XIX° siècle. Les interventions subséquentes des architectes Painter et Maxwell et de la firme ARCOP ont respecté l'esprit initial de sa sihouette imposante, qui est l'un des points dominants du Vieux-Québec. Commission des lieux et monuments historiques du Canada. Gouvernement du Canada.
Peinture, Céphalopodes, Biologie marine, Symétrie (art), Octopus vulgaris, Ernst Haeckel (1834-1919), Poulpe commun, Symétrie (biologie)
Poulpe commun
Pieuvre commune ou poulpe commun (Octopus vulgaris). Planche 54 de "Formes artistiques de la Nature" (Kunstformen der Natur), 1904, livre de lithographies illustratives de sciences naturelles publié par le biologiste allemand Ernst Haeckel (1834-1919) dont les représentations eurent une influence décisive sur le courant de l'Art nouveau au début du XXe siècle, et notamment l'École de Nancy. Cinq céphalopodes "Gamochonia, Trichterkraken".
Peinture, Céphalopodes, Biologie marine, Art nouveau (décoration), Symétrie (art), Octopus vulgaris, Ernst Haeckel (1834-1919), Poulpe commun, Symétrie (biologie)
Poulpe commun
Poulpe commun (Octopus vulgaris). Planche 54 de "Formes artistiques de la Nature" (Kunstformen der Natur), 1904, livre de lithographies illustratives de sciences naturelles publié par le biologiste allemand Ernst Haeckel (1834-1919) dont les représentations eurent une influence décisive sur le courant de l'Art nouveau au début du XXe siècle, et notamment l'École de Nancy. Cinq céphalopodes "Gamochonia, Trichterkraken".
Peinture, Poulpes, Biologie marine, Art nouveau (décoration), Symétrie (art), Pieuvres, Ernst Haeckel (1834-1919), Symétrie (biologie)
Poulpe Pinnoctopus cordiformis
Planche 54 de "Formes artistiques de la Nature" (Kunstformen der Natur), 1904, livre de lithographies illustratives de sciences naturelles publié par le biologiste allemand Ernst Haeckel (1834-1919) dont les représentations eurent une influence décisive sur le courant de l'Art nouveau au début du XXe siècle, et notamment l'École de Nancy. Pieuvre (Pinnoctopus cordiformis).
Gravure, Walter Crane (1845-1915), Symétrie (art), Arts décoratifs, Tutoriels, Dessin -- Étude et enseignement, Dessin décoratif -- Motifs végétaux
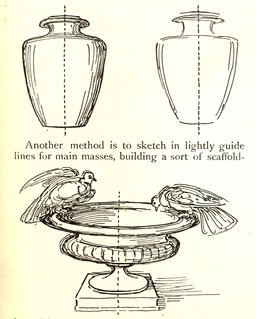
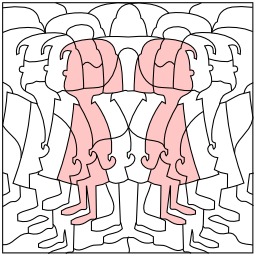
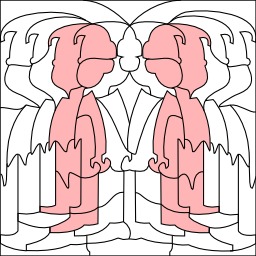
Remplissage de forme carrée
Walter Crane, Line and Form, page 80 : remplissage d'une forme carrée.
Photographie, Dix-neuvième siècle, Cercles, Symétrie (art), Londres (GB), Architecture, Dômes, Rosaces (vitraux)
Rosace à Londres
Dome et rosace du hall d'entrée de la National Gallery à Londres. Elle fut fondée en 1824 et possède rès de 2 300 tableaux. Le bâtiment actuel à Trafalgar Square est l'oeuvre de l'architecte William Wilkins (1832–38). L'entrée est l'oeuvre de Sir John Taylor (1884–7).
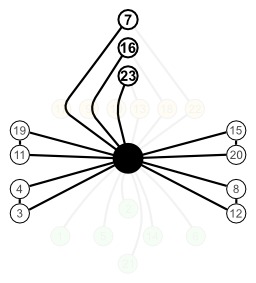
Rotations du tétraèdre
Rotations du tétraèdre : Tout groupe de symétrie dont les éléments ont un point fixe commun, ce qui est vrai pour tous les groupes de symétrie de figures bornées, peut être représenté comme un sous-groupe du groupe orthogonal O(n) en choisissant comme origine un point fixe. Le groupe de symétrie propre est alors un sous-groupe du groupe spécial orthogonal SO(n), c'est pourquoi il est aussi appelé le groupe de rotation de la figure.
Dessins et plans, Neige, Dix-septième siècle, Savants français, Savants allemands, Johannes Kepler (1571-1630), Hexagones, Symétrie, Symétrie (physique), Cristallographie, Cristaux de neige, Astronomes, René Descartes (1596-1650)
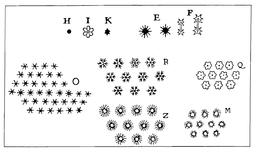
Schémas de cristaux de neige par Descartes
Schémas de cristaux de neige par René Descartes (1596-1650), à partir de l'ouvrage de Johannes Kepler (1571-1630). En 1611, Kepler publie "L’Étrenne ou la neige sexangulaire", premier traité scientifique de 24 pages qui étudie les cristaux de neige, observant notamment leur symétrie hexagonale. René Descartes observe en 1635 à l'œil nu des cristaux de neige et décrit notamment des formes rares, cristaux à douze branches, plaques hexagonales et colonnes.
Photographie, Géométrie, Nouvelle-Calédonie, Serres, Paris (France) -- Quartier du Jardin des Plantes, Symétrie (art), Architecture, Serres chaudes
Serre tropicale de la Nouvelle-Calédonie
Composition géométrique à partir de la serre tropicale de la Nouvelle-Calédonie restaurée et réouverte au public en 2010, au Jardin des Plantes de Paris 15 septembre 2010.
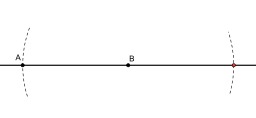
Symétrique d'un point par rapport à un point
Construction du symétrique d'un point A par rapport à un point B, à la règle et au compas.
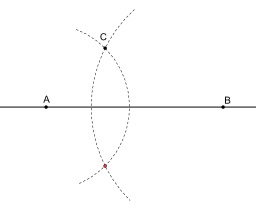
Symétrique d'un point par rapport à une droite
Construction du symétrique d'un point C par rapport à une droite à la règle et au compas : Le symétrique du point C par rapport à la droite (AB) s'obtient en construisant le point d'intersection (différent de C) entre le cercle de centre A passant par C et le cercle de centre B et passant par C. Si le point C est sur la droite (AB), il est son propre symétrique et aucune construction n'est nécessaire.
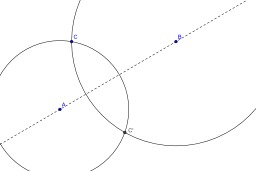
Symétrique d'un point par rapport à une droite
Construction au compas seul du symétrique d'un point par rapport à une droite. Le symétrique du point C par rapport à la droite (AB) est le point d'intersection des cercles de centres A et B et passant par C. Dans la construction la droite (AB) est tracée en pointillés pour permettre de suivre le raisonnement mais elle ne sert pas en tant que telle dans la construction. En géométrie classique plane, le théorème de Mohr Mascheroni, démontré par Georg Mohr en 1672 et par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas seul (sauf le tracé effectif des droites). Est considéré comme constructible tout point d'intersection de deux cercles dont les centres sont des points déjà construits et dont les rayons sont des distances entre des points déjà construits.
Trapézoèdre hexagonal
Trapézoèdre hexagonal. La partie n-gonale du nom ne fait pas référence aux faces mais à l'arrangement des sommets autour d'un axe de symétrie. L'antiprisme dual n-gonal possède deux faces n-gonales. Un trapézoèdre n-gonal peut être décomposé en deux pyramides n-gonales égales et un antiprisme n-gonal.
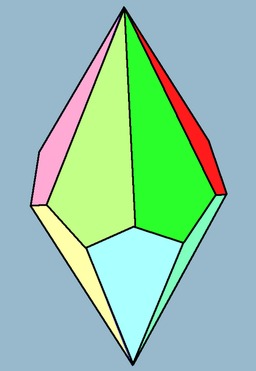
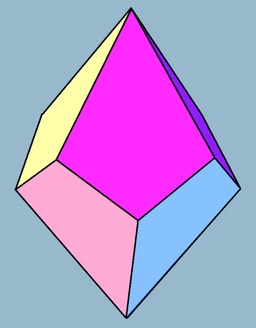
Trapézoèdre tétragonal
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces, par exemple le trapézoèdre tétragonal. Le nom trapézoèdre est trompeur puisque les faces ne sont pas des trapèzes. Le trapézoèdre ou antidiamant ou deltoèdre n-gonal est le polyèdre dual d'un antiprisme n-gonal régulier. Ses 2n faces sont des deltoïdes congrus (ou cerfs-volants). Les faces sont décalées symétriquement.
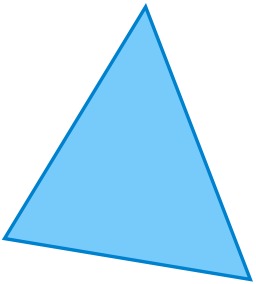
Triangle
Un triangle scalène : un triangle qui n'est ni isocèle (ce qui exclut également le cas équilatéral) ni plat est dit scalène (du grec σκαληνός (skalenos) : boiteux, inégal, déséquilibré, oblique...) Il s'agit donc d'un triangle ayant trois côtés de longueurs différentes, trois angles de mesures différentes et aucun axe de symétrie.
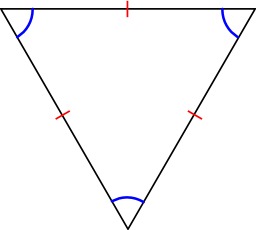
Triangle equilateral
Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur. Ses trois angles ont alors la même mesure qui vaut donc 60° et il admet trois axes de symétrie.
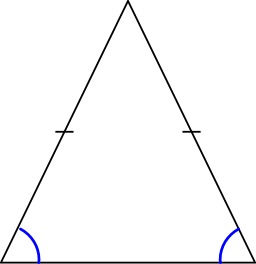
Triangle isocele
Un triangle isocèle est un triangle ayant au moins deux côtés de même longueur. Les deux angles adjacents au troisième côté sont alors de même mesure. Réciproquement, tout triangle ayant deux angles de même mesure est isocèle. Les triangles isocèles sont les seuls à admettre un axe de symétrie en dehors des triangles plats.
Triskèle
Le triskèle, également orthographié triskell ou triskel ou appelé aussi triquètre ou triscèle (du grec τρισκελης, « triskélès » qui signifie à « trois jambes ») est un symbole représentant trois jambes humaines (triskèle du premier type), ou aussi de trois spirales entrecroisées (triskèle du second type) ou tout autre symbole avec trois protubérances évoquant une symétrie de groupe cyclique. Bien qu'il soit apparu dans diverses cultures et à différentes périodes, il est considéré comme une caractéristique importante de l'art celtique à l'époque de la Tène (second âge du fer, Ve - IIe siècle av. J.-C.). On le trouve déjà sous forme de gravure sur une grande pierre du tombeau néolithique de Newgrange, sur le site de Brú na Bóinne, en Irlande.
Photographie, Papillons, Réflexion (optique), Symétrie (art), Belle-dame (animaux), Vanesse du chardon, Symétrie (biologie), Vanessa cardui
Vanesse du chardon
Vanesse du chardon (Vanessa cardui). Les deux ailes des papillons sont symétriques par réflexion : l'une est comme l'image dans un miroir de l'autre.