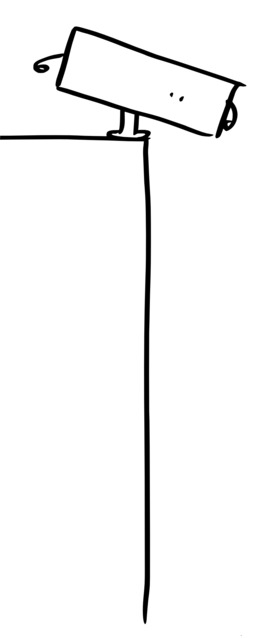Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Cube, Carré, Géométrie des nombres, Gnomonique, Abu Bakr Muhammad ibn al-Hasan al- Karaji (....-1019 ?)
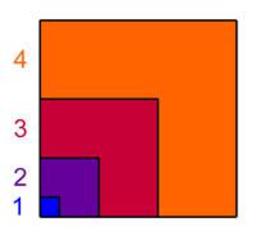
Carré d'un nombre triangulaire
Démonstration géométrique de la formule donnant le carré d'un nombre triangulaire, égal à la somme des premiers cubes parfaits : le carré du nième nombre triangulaire est égal à la somme des n premiers cubes. L'illustration géométrique permet de se convaincre de la véracité de ses propositions. L'aire de la zone orange de la figure est appelée nombre gnomonique. Elle est constituée de deux rectangles de base 4 et de côté le nombre triangulaire d'indice 4, c'est-à-dire 10. Ces deux rectangles se recoupent sur un carré de côté 4, on en déduit que l'aire orange est égale à 5 x 4 x 4 - 4 x 4, ou encore 43. Ce raisonnement est valable sur chaque nombre gnomonique, l'aire du carré de côté le nombre triangulaire d'indice 4 est égal la somme des 4 premiers cubes. De cette démonstration d'Al-Karaji, on déduit la première proposition.
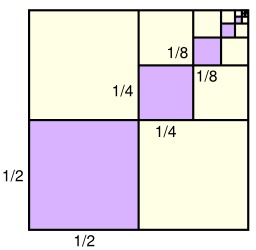
Carrés géométriques
Illustration de l'égalité 1/4 + 1/16 + 1/64 + 1/256 + ⋯ = 1/3 : chacun des carrés violets mesure 1/4 de la surface du grand carré le plus proche (1/2×1/2 = 1/4, 1/4×1/4 = 1/16, etc.). Par ailleurs, la somme des aires des carrés violets est égale à un tiers de la superficie du grand carré.
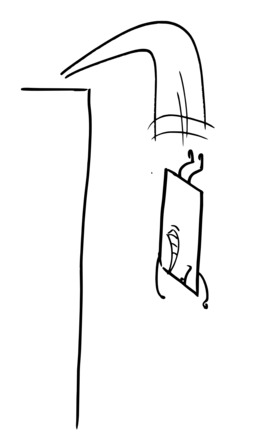
Dernière tentative de saut d'Hervé le carré
Dernière tentative de saut d'Hervé le carré, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hervé fait la roulade
Hervé fait la roulade, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Déclaration, Cercles, Formes (mathématiques), Odysseus, Personnages imaginaires, Cour amoureuse, Explication
Hervé l'ex-carré et Cléandre l'ex-ronde s'expliquent
Hervé l'ex-carré et Cléandre l'ex-ronde s'expliquent, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Surprise, Humour, Cercles, Formes (mathématiques), Transformation, Dessin en noir et blanc, Odysseus, Personnages imaginaires
Hervé l'ex-carré retrouve Cléandre l'ex-ronde
Hervé l'ex-carré retrouve Cléandre l'ex-ronde, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Personnages de bandes dessinées, dessins animés, etc., Sourire, Humour, Formes (mathématiques)
Hervé le carré
Hervé le carré, héros de "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Coeur, Humour, Relations amoureuses, Formes (mathématiques), Odysseus, Personnages imaginaires, Coeur (folklore)
Hervé le carré a le coeur brisé
Hervé le carré a le coeur brisé, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Angles, Humour, Formes (mathématiques), Dessin en noir et blanc, Odysseus, Personnages imaginaires
Hervé le carré a perdu tous ses angles
Hervé le carré a perdu tous ses angles, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hervé le carré a une idée pour s'arrondir
Hervé le carré a une idée pour s'arrondir, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Humour, Pentes et versants, Formes (mathématiques), Dessin en noir et blanc, Odysseus, Personnages imaginaires
Hervé le carré arrive en bas de la pente
Hervé le carré arrive en bas de la pente, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Humour, Pentes et versants, Formes (mathématiques), Odysseus, Onomatopées, Personnages imaginaires
Hervé le carré atterrit en bas de la pente
Hervé le carré atterrit en bas de la pente, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Formes (mathématiques), Odysseus, Collines, Personnages imaginaires
Hervé le carré au sommet de la colline
Hervé le carré au sommet de la colline, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Humour, Formes (mathématiques), Odysseus, Personnages imaginaires
Hervé le carré décide de s'arrondir
Hervé le carré décide de s'arrondir, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
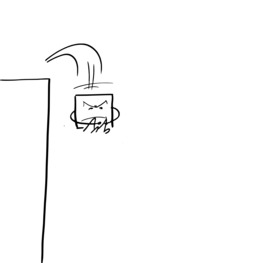
Hervé le carré est furieux
Hervé le carré est furieux, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Pentes et versants, Formes (mathématiques), Écologie des falaises, Inquiétude, Odysseus, Personnages imaginaires
Hervé le carré est inquiet
Hervé le carré est inquiet, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hervé le carré est perplexe
Hervé le carré est perplexe, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Émotions, Surprise, Cercles, Formes (mathématiques), Dessin en noir et blanc, Odysseus, Personnages imaginaires
Hervé le carré est surpris
Hervé le carré est surpris, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hervé le carré est triste
Hervé le carré est triste, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Relations amoureuses, Cercles, Formes (mathématiques), Odysseus, Personnages imaginaires, Âmes soeurs (relations amoureuses)
Hervé le carré et Cléandre la ronde se retrouvent
Hervé le carré et Cléandre la ronde se retrouvent, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Formes (mathématiques), Odysseus, Collines, Personnages imaginaires
Hervé le carré et la colline du Trapèze
Hervé le carré et la colline du Trapèze, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Humour, Pentes et versants, Formes (mathématiques), Odysseus, Onomatopées, Personnages imaginaires
Hervé le carré glisse le long de la pente
Hervé le carré glisse le long de la pente, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Peur, Falaises, Formes (mathématiques), Odysseus, Personnages imaginaires, Hésitation
Hervé le carré hésite
Hervé le carré hésite, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Falaises, Formes (mathématiques), Sauts (athlétisme), Odysseus, Personnages imaginaires
Hervé le carré réfléchit avant de sauter
Hervé le carré réfléchit avant de sauter, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Cercle, Humour, Exclamation (linguistique), Relations amoureuses, Formes (mathématiques), Mots d'esprit et jeux de mots, Odysseus, Personnages imaginaires
Hervé le carré rencontre Cléandre la ronde
Hervé le carré rencontre Cléandre la ronde, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Humour, Pentes et versants, Formes (mathématiques), Odysseus, Personnages imaginaires
Hervé le carré roule le long de la pente
Hervé le carré roule le long de la pente, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Falaises, Odysseus, Onomatopées, Personnages imaginaires, Essais d'écrasement, Essais de compression
Hervé le carré s'écrase au sol
Hervé le carré s'écrase au sol, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Chutes (accidents), Formes (mathématiques), Odysseus, Onomatopées, Personnages imaginaires
Hervé le carré s'écrase au sol
Hervé le carré s'écrase au sol, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Falaises, Chute libre, Formes (mathématiques), Odysseus, Onomatopées, Personnages imaginaires
Hervé le carré s'écrase au sol et s'aplatit
Hervé le carré s'écrase au sol et s'aplatit, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Humour, Cercles, Formes (mathématiques), Transformation, Odysseus, Personnages imaginaires
Hervé le carré s'est arrondi
Hervé le carré s'est arrondi, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hervé le carré s'est transformé en parallélogramme
Hervé le carré s'est transformé en parallélogramme, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Colère, Polygones, Formes (mathématiques), Odysseus, Personnages imaginaires
Hervé le carré s'est transformé en pentagone
Hervé le carré s'est transformé en pentagone, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Humour, Formes (mathématiques), Sauts (athlétisme), Odysseus, Collines, Personnages imaginaires
Hervé le carré saute
Hervé le carré saute, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hervé le carré saute à la verticale
Hervé le carré saute à la verticale, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Falaises, Formes (mathématiques), Sauts (athlétisme), Odysseus, Personnages imaginaires
Hervé le carré saute dans le vide
Hervé le carré saute dans le vide, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Falaises, Colère, Formes (mathématiques), Odysseus, Cris, Personnages imaginaires, Sauts
Hervé le carré saute en hurlant
Hervé le carré saute en hurlant, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
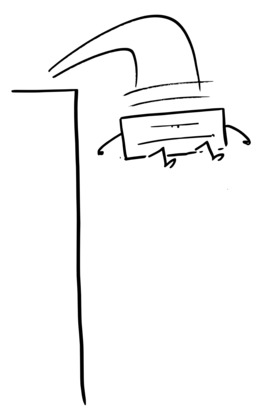
Hervé le carré saute pour la seconde fois
Hervé le carré saute pour la seconde fois, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hervé le carré se précipite dans le vide
Hervé le carré se précipite dans le vide, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Humour, Formes (mathématiques), Mots d'esprit et jeux de mots, Promenade, Personnages imaginaires
Hervé le carré se promène en Angle-Terre
Hervé le carré se promène en Angle-Terre, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Falaises, Formes (mathématiques), Odysseus, Onomatopées, Personnages imaginaires, Échec
Hervé le carré se transforme en losange
Hervé le carré se transforme en losange, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Coeur, Humour, Relations amoureuses, Formes (mathématiques), Coeur -- Folklore, Personnages imaginaires
Hervé le carré tombe amoureux de Cléandre la ronde
Hervé le carré tombe amoureux de Cléandre la ronde, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hervé revient à la colline du trapèze
Hervé revient à la colline du trapèze, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Photographie, Calcul, Carré, Jeux mathématiques, Dominos (jeu), Matériel didactique, Vulgarisation scientifique, Écrivains russes pour la jeunesse, Matériel pédagogique, Intellectuels russes, Yakov Perelman (1882-1942)
Jeu mathématique avec des dominos
Un des carrés possibles du jeu de Yakov Perelman (1882-1942), professeur russe : quatre dominos formant un carré sont disposés de façon à ce que le nombre de points de chacun des cotés soit identique.
Dessins et plans, Géométrie, Couleurs, Tapis, Carré, Mathématiciens, Savants polonais, Wacław Sierpinski (1882-1969), Fractales
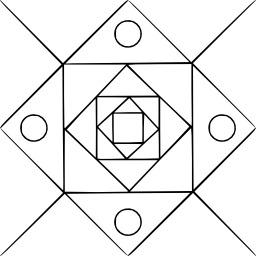
Le carré de Sierpinski
Le tapis de Sierpiński (1916), du nom de Wacław Sierpiński (1882-1969), est une fractale obtenue à partir d'un carré. Le tapis se fabrique en découpant le carré en neuf carrés égaux avec une grille de trois par trois, et en supprimant la pièce centrale, et en appliquant cette procédure indéfiniment aux huit carrés restants.
Mandala de Sable 03
Premier jour de la réalisation d'un mandala de sable "Pour la paix dans le monde", par trois lamas du temple des Mille Bouddhas, à la Tour de la Liberté de Saint-Dié-des-Vosges, les 11, 12 et 13 avril 2008 : le carré et ses quatre portes, le cercle central.
Mandala de Vajradhatu
Mandala de Vajradhatu (boudhisme tibétain) du XIXème siècle : forme de base carrée avec quatre portes d'entrée, contenant un cercle et un centre (symétrie centrale).
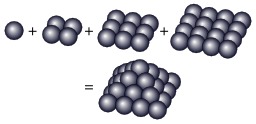
Nombre pyramidal carré 30
Représentation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16.