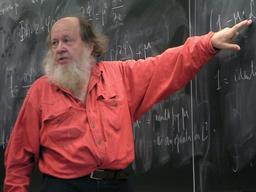Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Rubans, Bouteilles, Mathématiciens, Ferdinand Möbius (1790-1868), Felix Klein (1849-1925)
Bouteille de Klein
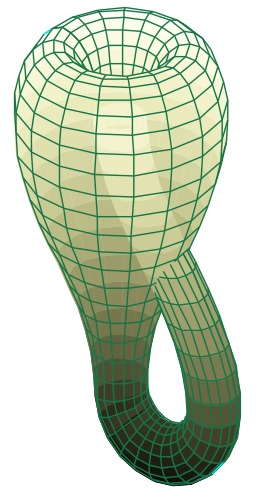
Vue de la bouteille de Klein dans un espace à trois dimensions. En mathématiques, la bouteille de Klein (prononcé kla.in) est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle il n'est pas possible de définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein (1849-1925). Elle est étroitement liée au ruban de Möbius.
Photographie, Bouteilles, Mathématiciens, Noeuds et épissures, Travail du verre, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Felix Klein (1849-1925)
Bouteille de Klein en verre
Réalisation de l'immersion de la bouteille de Klein, en verre. On peut en quelque sorte considérer que la bouteille de Klein est une surface qui fait un « nœud ». En tant que surface (objet à 2 dimensions), il lui faut 4 dimensions pour faire un nœud, de même que pour une courbe (objet à une dimension) il faut 3 dimensions pour faire un nœud.
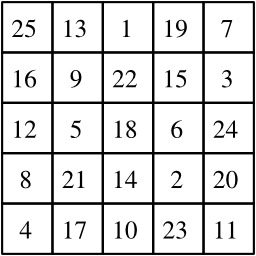
Carré magique selon Moschopoulos
Un carré magique d'ordre 5 construit selon la méthode de Moschopoulos. La méthode de construction proposée par le Byzantin Manuel Moschopoulos, dite « parcours en cavalier d'échecs », se représente par le vecteur déplacement (1, 2) et le vecteur collision (1 + 1, 2 - 2) = (2, 0).
Dessins et plans, Fruits, Citrons, Mathématiciens, Infographie, Images de synthèse, Formules mathématiques, Oberwolfach (Allemagne), Scientifiques autrichiens
Citron imaginaire
Citron imaginaire : exposition itinérante "IMAGINARY" de l'institut de mathématiques d'Oberwolfach en Allemagne, d'après une surface algébrique inventée par Herwig Hauser, mathématicien autrichien né en 1959. La formule d'origine est x^2+z^2+y^3(1-y)^3=0.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Claude-Gaspard Bachet (1581-1638)
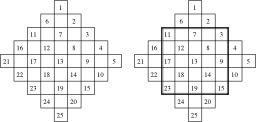
Construction d'un carré magique - 1
Construction d'un carré magique 5x5, méthode de Méziriac : Premières étapes de construction d'un carré magique d'ordre 5. Chaque diagonale allant de gauche à droite comporte un entier unique en ordre croissant. Ensuite, le contour du carré magique final est esquissé.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Claude-Gaspard Bachet (1581-1638)
Construction d'un carré magique - 2
Dernières étapes de la construction d'un carré magique 5x5 selon la méthode de Méziriac.
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
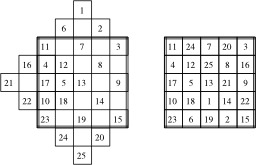
Construction d'un carré magique par la méthode du losange - 1
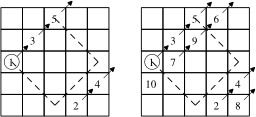
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
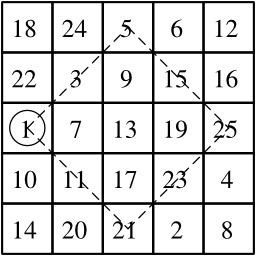
Construction d'un carré magique par la méthode du losange - 2
Un carré magique 5x5 construit selon la méthode du losange proposée par John Horton Conway : Le résultat final est un carré magique dont la constante est 65.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Siam, Simon de La Loubère (1643-1729)
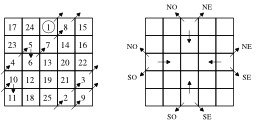
Construction d'un carré magique selon la méthode siamoise
Un carré magique d'ordre 5 avec un carré adjacent montrant des directions : construction d'un carré magique d'ordre impair selon la méthode siamoise. Dans cet exemple, le carré est rempli selon les diagonales nord-est (NE), mais elles pourraient être parallèles à sud-est (SE), à sud-ouest (SO) ou à nord-ouest (NO). 1) Placer le 1 tel que montré. 2) Décaler d'une case vers la droite puis d'une case vers le haut pour le 2, et ainsi de suite pour le 3, puis le 4, etc. 3) Si la pointe de la flèche sort du carré, revenir de l'autre côté, comme si le carré était enroulé sur un tore. 4) Si la prochaine case est occupée, décaler d'une case vers le bas. La méthode siamoise a été introduite en France par Simon de La Loubère en 1688 alors qu'il revenait de son ambassade au Siam. Source : http://fr.wikipedia.org/wiki/Carr%C3%A9_magique_%28math%C3%A9matiques%29.
Dessins et plans, Géométrie, Jeux mathématiques, Jeux de logique, Mathématiciens, Devinettes et énigmes, Casse-tête logique, Énigmes mathématiques, Henry Dudeney (1857-1930)
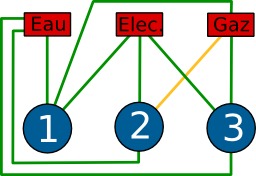
Enigme des 3 maisons
Enigme des trois maisons : Une solution généralement non admise dans l'énigme des trois maisons puisque les canalisations de gaz et d'électricité se croisent. Enigme posée en 1917 par Henry Dudeney (1857-1930) en ces termes : "Un lotissement de trois maisons doit être équipé d'eau, de gaz et d'électricité. La règlementation interdit de croiser les canalisations pour des raisons de sécurité. Comment faut-il faire ?"
Dessins et plans, Géométrie, Triangle, Mathématiciens, Itération (mathématiques), Algorithmes, Savants polonais, Wacław Sierpinski (1882-1969), Fractales, Récursivité, Théorie de la
Évolution du triangle de Sierpinski
Évolution du triangle de Wacław Sierpinski (1882-1969) en 5 itérations. Un algorithme pour obtenir des approximations arbitrairement proches du triangle de Sierpiński peut s'écrire de la manière suivante : 1-Commencer à partir d'un triangle quelconque du plan. Le triangle canonique de Sierpiński se construit à partir d'un triangle équilatéral ayant une base parallèle à l'axe des abscisses ; 2-Tracer les trois segments qui joignent deux à deux les milieux des côtés du triangle, ce qui délimite 4 nouveaux triangles ; 3-Enlever le petit triangle central. Il y a maintenant trois petits triangles qui se touchent deux à deux par un sommet, dont les longueurs des côtés sont la moitié de celles du triangle de départ (obtenue par une homothétie de rapport 1/2), et dont l'aire est divisée par 4. 4-Recommencer à la deuxième étape avec chacun des petits triangles obtenus.
Peinture, Moines, Compas, Physiciens, Galilée (1564-1642), Héliocentrisme, Physiciens italiens, Mathématiciens, Inventeurs, Astronomes, Art mexicain, Globe terrestre, Reconstitutions historiques, Padoue (Italie)
Galilée à l'Université de Padoue
Félix Parra, Galilée démontre les Nouvelles Théories Astronomiques à l'Université de Padoue, 1873. Galilée est un mathématicien, géomètre, physicien et astronome italien du XVIIe siècle mort à 77 ans. Parmi ses réalisations techniques, il a inventé la lunette astronomique, perfectionnement de la découverte hollandaise d'une lunette d'approche, pour procéder à des observations rapides et précoces qui ont bouleversé les fondements de la discipline astronomique. Félix Parra (1845 - 1919) est un peintre mexicain. Source : http://fr.wikipedia.org/wiki/Galil%C3%A9e_%28savant%29
Dessins et plans, Musique -- Intervalles et gammes, Mathématiciens, Solfège, Son, Musique en muséologie, Philosophes grecs dans l'Antiquité, Pythagore (0580?-0500? av. J.-C.)
Gamme pythagoricienne en solfège
Construction de la gamme pythagoricienne en solfège, avec 12 quintes ascendantes ramenées dans la même octave. On descend chaque fois que possible d'une octave afin de rester dans la même (représentée en bleu ciel). Pythagore (0580?-0500? av. J.-C.) est un philosophe et mathématicien grec.
Textes, Dix-neuvième siècle, Mathématiciens, Poésie, Vers alexandrin, Alphonse Rebière (1842−1901), Savants grecs
Histoire de π
Poème pour la mathématiciens grecs du nombre π, par Alphonse Rebière, Mathématiques et mathématiciens, 1898 (p. 399) : Pythagore et Archimède. 132 mots, 20 alexandrins.
Dessins et plans, Musique -- Intervalles et gammes, Mathématiciens, Solfège, Son, Musique en muséologie, Philosophes grecs dans l'Antiquité, Accords (musique), Pythagore (0580?-0500? av. J.-C.)
Intervalles de la gamme pythagoricienne
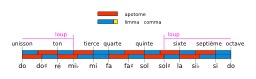
Représentation graphique d'une gamme pythagoricienne : il est possible de représenter une gamme pythagoricienne particulière en mettant les apotomes et les limmas les uns à la suite des autres selon les intervalles obtenus, le limma étant plus court que l'apotome d'un comma. Les deux demi-tons, qui sont identiques dans la gamme tempérée, sont nommés dans la gamme pythagoricienne : apotome, pour l'intervalle formé par une note et sa version altérée ; limma, pour l'intervalle formé par une note altérée et la note voisine ne portant pas le même nom. Ces intervalles sont disposés ainsi : do - apotome - do♯ - limma - ré, pour les quintes ascendantes ; do - limma - ré♭ - apotome - ré, pour les quintes descendantes. Dans la gamme pythagoricienne, les notes bémolisées sont inférieures d'un comma pythagoricien à leurs notes conjointes diésées, on en déduit l'ordre suivant : do - ré♭ - do♯ - ré. Source : http://fr.wikipedia.org/wiki/Accord_pythagoricien
Dessins et plans, Géométrie, Couleurs, Tapis, Carré, Mathématiciens, Savants polonais, Wacław Sierpinski (1882-1969), Fractales
Le carré de Sierpinski
Le tapis de Sierpiński (1916), du nom de Wacław Sierpiński (1882-1969), est une fractale obtenue à partir d'un carré. Le tapis se fabrique en découpant le carré en neuf carrés égaux avec une grille de trois par trois, et en supprimant la pièce centrale, et en appliquant cette procédure indéfiniment aux huit carrés restants.
Dessins et plans, Géométrie, Jeux mathématiques, Pavages (mathématiques), Mathématiciens, Tuiles, Divertissements mathématiques
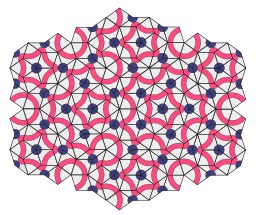
Pavage de Penrose avec tuiles apériodiques
Pavage de Penrose réalisé avec deux tuiles apériodiques. Roger Penrose est un mathématicien anglais. Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement. Plus généralement toute portion finie du pavage, aussi grande soit-elle, se répète infiniment dans le pavage. Les pavages de Penrose ne seraient restés qu'un joli divertissement mathématique si n'avaient été découverts, en 1984, des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux. Les pavages non périodiques, en particulier ceux de Penrose, s'avérèrent alors un modèle plausible de ces étranges matériaux. Cette découverte illustra à nouveau ce que Roger Penrose lui-même avait déjà remarqué en 1973, à propos d’un sujet de relativité générale : « On ne sait jamais vraiment quand on perd son temps ». Source : http://fr.wikipedia.org/wiki/Pavage_de_Penrose.
Peinture, Calculatrices, Mathématiciens, Inventeurs, Charles Xavier Thomas de Colmar (1785-1870), Machines à calculer
Portrait de Charles Xavier Thomas de Colmar
Charles Xavier Thomas de Colmar (1785-1870), portrait au château de Maisons-Laffitte : inventeur de la première machine à calculer industrielle : l’arithmomètre Thomas.
Peinture, Physiciens, Dix-septième siècle, Savants français, Mathématiciens, Parchemin, Inventeurs, Peinture de portraits (17e siècle), Machines à vapeur, Denis Papin (1647-1712?)
Portrait de Denis Papin en 1689
Portrait de Denis Papin (1647-1712?) en 1689, tenant un rouleau représentant son "digesteur" de 1689. Physicien, mathématicien et inventeur français, un des précurseurs de l'invention de la machine à vapeur, qui eu l'idée du piston (dés 1690), et inspira la machine que l'Anglais Thomas Newcomen (1664-1729) mit au point ensuite (en 1712). Calviniste, il quitta définitivement la France, après la révocation de l'Édit de Nantes (1685) et occupa une chaire de mathématiques à l'Université de Marburg, Allemagne (1687). Source : http://fr.wikipedia.org/wiki/Denis_Papin
Portrait de Gaspard Monge
Le tour de la France par deux enfants, par George Bruno, pseudonyme d'Augustine Fouillée (née Tuillerie), 1877, p.108 ; manuel scolaire, édition de 1904 : Gaspard MONGE (1746-1818), mathématicien français dont l'œuvre considérable mêle géométrie descriptive, analyse infinitésimale et géométrie analytique. En parallèle à ses travaux de recherche, il enseigne une grande partie de sa vie et a comme élèves beaucoup des futurs grands mathématiciens français du XIXe siècle. Il joue un grand rôle dans la Révolution française, tant du point de vue politique que du point de vue de l'instauration d'un nouveau système éducatif : il participe à la création de l'École normale de l'an III et de l'École polytechnique (en 1794), deux écoles où il enseigne la géométrie. Il concourt également avec Berthollet, Chaptal et Laplace à la création de l'École d'arts et métiers. Il est également membre de la commission des sciences et des arts lors de la campagne d'Italie (1796-1797), et chargé de mission dans l'expédition d'Égypte (1798-1799). Le 12 décembre 1989, ses cendres ont été transférées au Panthéon.
Gravure, Médecins, Renaissance, Seizième siècle, Philosophes, Mathématiciens, Inventeurs, Humanistes de la Renaissance, Astrologues, Francesco Gonin (1808–1889), Girolamo Cardano (1501-1576), Mages
Portrait de Girolamo Cardano
Portrait de Girolamo Cardano (1501-1576) par Francesco Gonin (1808–1889) : Girolamo Cardano, (1501-1576), est un mathématicien, un philosophe, un astrologue, un inventeur, et un médecin italien. Inventa le procédé mécanique de rotation non rectiligne sur un arbre de transmission : le cardan. Source : http://fr.wikipedia.org/wiki/Girolamo_Cardano
Photographie, Mathématiciens, Enseignants, Professeurs, Professeurs (enseignement supérieur), Professeurs de mathématiques
Professeur de mathématiques au tableau
Professeur de mathématiques au tableau : Adrien Douady à l'IHP, en 2003.
Dessins et plans, Géométrie, Douze (le nombre), Cinq (le nombre), Mathématiciens, Polygones, Numération, Un (le nombre), Léonard Euler (1707-1783), Vingt-deux (le nombre)
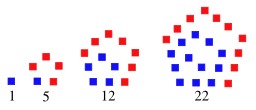
Quatre nombres pentagonaux
Un nombre pentagonal est un nombre figuré qui peut être représenté par un pentagone. Les premiers nombres pentagonaux sont : 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001. Les nombres pentagonaux sont importants dans la théorie des partages d'entiers d'Euler, et ils interviennent par exemple dans son théorème des nombres pentagonaux. Source : http://fr.wikipedia.org/wiki/Nombre_pentagonal
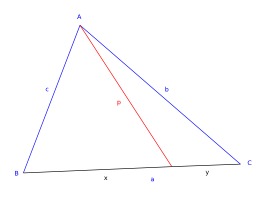
Théorème de Stewart
En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane, due au mathématicien Matthew Stewart dans les années 1746 : Théorème — Soit p une cévienne d'un triangle ABC divisant en X le côté a en deux parties x et y. On a alors la relation suivante : acdot (xy+p^{2}) = xcdot b^{2}+ycdot c^{2}. Matthew Stewart est un mathématicien écossais (1717-1785) reconnu comme un mathématicien important après la publication de son "General Theorems", en 1746.