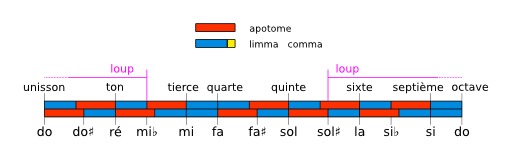
Intervalles de la gamme pythagoricienne

Description de la ressource

Représentation graphique d'une gamme pythagoricienne : il est possible de représenter une gamme pythagoricienne particulière en mettant les apotomes et les limmas les uns à la suite des autres selon les intervalles obtenus, le limma étant plus court que l'apotome d'un comma. Les deux demi-tons, qui sont identiques dans la gamme tempérée, sont nommés dans la gamme pythagoricienne : apotome, pour l'intervalle formé par une note et sa version altérée ; limma, pour l'intervalle formé par une note altérée et la note voisine ne portant pas le même nom. Ces intervalles sont disposés ainsi : do - apotome - do♯ - limma - ré, pour les quintes ascendantes ; do - limma - ré♭ - apotome - ré, pour les quintes descendantes. Dans la gamme pythagoricienne, les notes bémolisées sont inférieures d'un comma pythagoricien à leurs notes conjointes diésées, on en déduit l'ordre suivant : do - ré♭ - do♯ - ré. Source : http://fr.wikipedia.org/wiki/Accord_pythagoricien

Détails de la ressource

• Déposé par : Anne-Marie Lesca, le 2014-07-03
• Auteur : Romainbehar
• Origine : http://commons.wikimedia.org/wiki/File:Intervalles_de_la_gamme_pythagoricienne.svg
• Licence : gfdl
• Format : image/svg+xml
• Type :
• Collection :
• Description ScolomFR : http://data.abuledu.org/LOM/doc0000020900.xml

Téléchargement

512 - 1024 - Fichier Original - Source + Métadonnées SCOLOMFR

Relations et mots clés

Dessins et plans, Musique -- Intervalles et gammes, Mathématiciens, Solfège, Son, Musique en muséologie, Philosophes grecs dans l'Antiquité, Accords (musique), Pythagore (0580?-0500? av. J.-C.)