Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, animaux prédateurs, Populations, Probabilités, Prédateurs et proies, Biologie des populations, Équations, Équations d'évolution, Équations différentielles
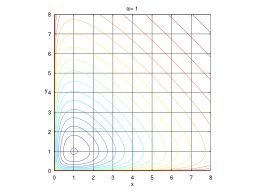
Équations proie-prédateur de Lotka-Volterra
Courbes d'évolution d'un système complexe, formé de deux espèces, proie et prédateur : équations de Lotka-Volterra. L'effectif des proies est x(t), celui des prédateurs y(t) . On retombe sur le cas précédent si y est nul. La quantité x(t)y(t) est une probabilité de rencontre, qui influe négativement sur une population (les proies), positivement sur l'autre (les prédateurs). À chaque instant, connaissant les populations en présence, on peut décrire la tendance. Ces deux équations sont couplées c'est-à-dire qu'il faut les résoudre ensemble. Mathématiquement, il faut les concevoir comme une seule équation d'inconnue le couple (x(t),y(t)) . Si l'effectif initial des populations est connu, l'évolution ultérieure est parfaitement déterminée. Elle se fait le long d'une des courbes d'évolution figurées ci-contre, qui laissent apparaître un comportement cyclique.
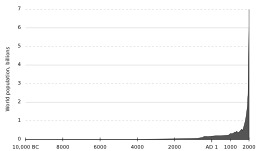
Évolution de la population mondiale depuis la préhistoire
Estimation de l'évolution de la population mondiale depuis la Préhistoire jusqu'en 2000. Légende en anglais : "world population, billions" = population mondiale en billions ; BC = avant JC. ; AD = après JC.
Dessins et plans, Environnement, Bonheur, Géographie, Populations, Cartes mondiales, Espérance de vie, Bien-être, Contribution au concept de bonheur, Écologie des populations, Économie du bien-être, Efficience écologique, Empreinte écologique, Environnement -- Cartographie
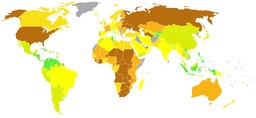
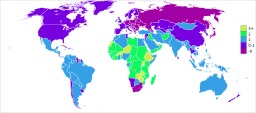
La planète du bonheur
Carte mondiale des pays du bonheur, selon les critères du HPI : L'indice de la planète heureuse (Happy Planet Index) est un indicateur économique alternatif au PIB. Créé par un "think tank" britannique, la "New Economics Foundation" (NEF), le HPI prend en compte le bien-être humain et les incidences sur l'environnement. Il classe 178 pays d'après 3 indicateurs : l’empreinte écologique, l’espérance de vie et le degré de bonheur des populations. Ainsi, ce classement donne une image très différente de la richesse et de la pauvreté des nations. C'est un indicateur d'efficience écologique.
Dessins et plans, Populations, Écosystèmes, Biosphère, ADN, Biocénoses, Biocénoses -- Structure trophique, Biomes, Communautés, Compétition entre individus (biologie), Molécules, Organes, Paysages, Plantes -- Populations, Théories du vivant, Vie (biologie)
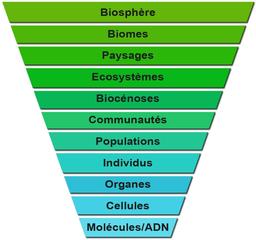
Niveau d'Organisation et d'Intégration du Vivant
Graphique représentant les différents niveaux d'organisation ou d'intégration du vivant. Il ne s'agit pas d'une hiérarchie, mais d'une présentation simplifiée, des niveaux étudiés par les biologistes et écologues : biosphère, biomes, paysages, écosystèmes, biocénoses, communautés, populations, individus, organes, cellules, molécules/ADN.
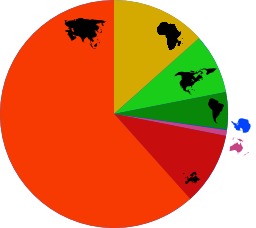
Répartition de la population mondiale par continent en 2007
Répartition de la population mondiale par continent en 2007 par diagramme ciculaire. Asie : 60,5% ; Afrique : 14% ; Europe : 11,3% ; Amérique latine et Caraïbes : 8,6% ; Amérique du Nord : 5,1% ; Océanie : 0,5%. Les régions les plus développées représentent 18,3 % de la population en 2007 contre 81,7 % pour les régions les moins développées.
Taux d'accroissement de la population mondiale en 2011
Taux d'accroissement de la population en 2011 (données CIA).
Dessins et plans, Populations, Répartition, Animaux -- Dispersion, Biologie des populations, Dispersion, Dispersion (botanique), Géographie de la population, Microorganismes -- Dispersion
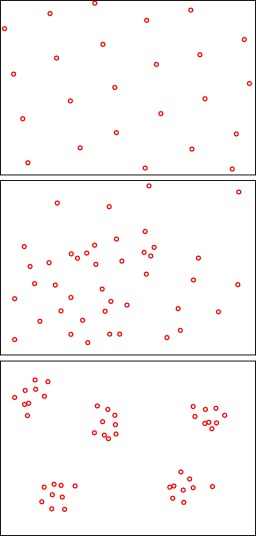
Trois types de distribution de la population
Les trois grands types de dispersion de la population. De haut en bas : la dispersion égale, la dispersion inégale et la dispersion insulaire. La distribution spatiale, en écologie, désigne l’arrangement spatial des organismes vivant dans leur milieu naturel. Elle peut aussi se définir comme la fluctuation spatiale de l’abondance des organismes dans leur aire de répartition1. Trois formes de dispersion sont généralement reconnues : égale, inégale et insulaire. La dispersion égale est celle où les organismes sont uniformément répartis dans l’espace. Les dispersions inégale et insulaire représentent les cas où les organismes ne sont pas uniformément répartis dans l’espace. La dispersion inégale donne une apparence d’arbitraire. Toutefois, les organismes sont très rarement dispersés arbitrairement dans un espace. Leur localisation est presque toujours étroitement influencée par divers facteurs biologiques et environnementaux. Dans la dispersion insulaire, les organismes forment des regroupements ou des îlots dans l’espace.