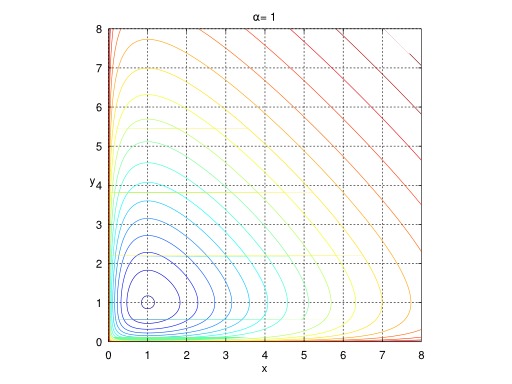
Équations proie-prédateur de Lotka-Volterra

Description de la ressource

Courbes d'évolution d'un système complexe, formé de deux espèces, proie et prédateur : équations de Lotka-Volterra. L'effectif des proies est x(t), celui des prédateurs y(t) . On retombe sur le cas précédent si y est nul. La quantité x(t)y(t) est une probabilité de rencontre, qui influe négativement sur une population (les proies), positivement sur l'autre (les prédateurs). À chaque instant, connaissant les populations en présence, on peut décrire la tendance. Ces deux équations sont couplées c'est-à-dire qu'il faut les résoudre ensemble. Mathématiquement, il faut les concevoir comme une seule équation d'inconnue le couple (x(t),y(t)) . Si l'effectif initial des populations est connu, l'évolution ultérieure est parfaitement déterminée. Elle se fait le long d'une des courbes d'évolution figurées ci-contre, qui laissent apparaître un comportement cyclique.

Détails de la ressource

• Déposé par : Anne-Marie Lesca, le 2012-12-05
• Auteur : Guillaume Jacquenot
• Origine : http://commons.wikimedia.org/wiki/File:Lotka_Volterra_Phase_plane_100.svg
• Licence : cc-by-sa
• Format : image/svg+xml
• Type : Dessins et plans
• Collection :
• Description ScolomFR : http://data.abuledu.org/LOM/doc0000005625.xml

Téléchargement

512 - 1024 - Fichier Original - Source + Métadonnées SCOLOMFR

Relations et mots clés

Dessins et plans, animaux prédateurs, Populations, Probabilités, Prédateurs et proies, Biologie des populations, Équations, Équations d'évolution, Équations différentielles