Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
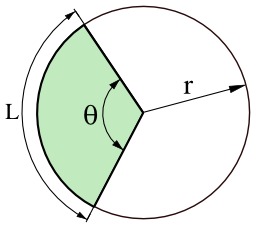
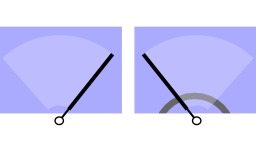
Arc de cercle
Cercle de rayon "r", arc de cercle de longueur "L" soustendu par un angle θ (theta) avec un secteur circulaire de surface "A".
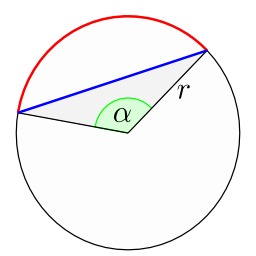
Arc et corde d'un cercle
Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Une corde (en bleu) est un segment de droite dont les extrémités se trouvent sur le cercle. Un arc est une portion de cercle délimitée par deux points (en rouge). Un secteur circulaire est une partie du disque comprise entre deux rayons. Un angle au centre (vert) est un angle formé par deux rayons du cercle.
Dessins et plans, Étoiles, Cinq (le nombre), Engrenages, Cercles, Épis de blé, Chine (République populaire), Roues dentées
Armoiries de la République populaire de Chine
Les armoiries de la République populaire de Chine représentent le Tian'anmen (la porte de la Paix céleste), entrée de la Cité interdite depuis la place Tian'anmen à Pékin, dans un cercle rouge. Au-dessus de cette représentation, on trouve les cinq étoiles également présentes sur le drapeau national. La bordure du cercle est décorée d'épis de blé, qui rappellent l'importance de l'agriculture et de la paysannerie dans l'idéologie maoïste. Au centre de la partie inférieure de la bordure se trouve une roue dentée qui symbolise le travail industriel. Source : http://fr.wikipedia.org/wiki/Embl%C3%A8me_de_la_R%C3%A9publique_populaire_de_Chine
Photographie, Bornes, Cercles, Winchester (GB), Mobilier urbain, Art contemporain, Art abstrait, Sonia Delaunay (1885-1979)
Borne anglaise peinte à la manière de Sonia Delaunay
Borne anglaise à Winchester peinte à la manière de Sonia Delaunay (1885-1979).
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres non-rationnels, Nombres transcendants, Pi (le nombre)
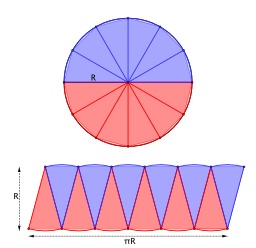
Calcul de l'aire du cercle avec Géogébra
Calcul de l'aire du cercle avec Géogébra : rayon x demi-circonférence. On déduit d’une propriété analogue pour les polygones réguliers que l’aire d’un cercle égale son demi-périmètre multiplié par son rayon. le périmètre du polygone est à peu près 2πr alors qu’en redistribuant les triangles formés on remarque que son aire est à peu près πr2. Pour formaliser le « à peu près » il faudrait faire tendre le nombre de côtés du polygone vers l’infini, ce qui illustre déjà la nature « analytique » de π.
Carottes multicolores
Carottes multicolores : Variétés des carottes sélectionnées pour leurs diverses couleurs. Certains des pigments responsables de ces couleurs sont bons pour la santé.
Cercles métalliques pour tonneaux
Empilements de cercles métalliques de tonneaux pour la mise en place des douelles : cercles de mise en place, plus épais et résistants pour le cintrage, le maintien, et la chauffe.
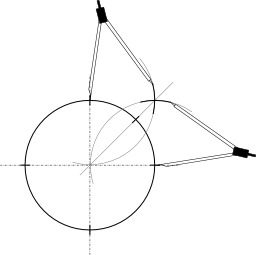
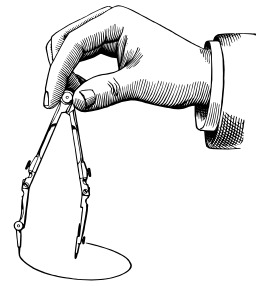
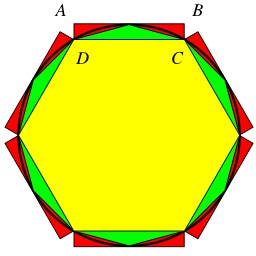
Construction d'un parallélogramme au compas
Construction au compas seul du quatrième point d'un parallélogramme : Les points A, B et C étant donnés, le quatrième point D du parallélogramme ABCD est le point d'intersection du cercle de centre A et de rayon BC et du cercle de centre C et de rayon BA non situé dans le demi-plan de frontière (CA) contenant B.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
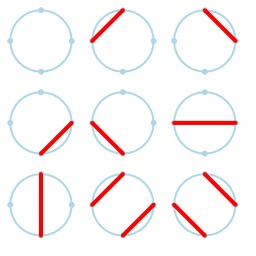
Cordes de Motzkin entre cinq points sur un cercle
Vingt-une cordes de Motzkin (qui ne se coupent pas) entre cinq points sur un cercle.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
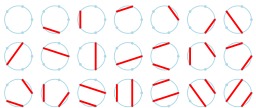
Cordes de Motzkin entre quatre points sur un cercle
Cordes de Motzkin sur un cercle : les neuf manières de dessiner des cordes qui ne se coupent pas entre quatre points d'un cercle. Le nombre de Motzkin est le nombre de façons de choisir des cordes ne se coupant pas, parmi les cordes reliant n points disposés sur un cercle. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas, Compas,
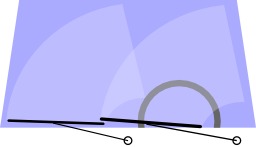
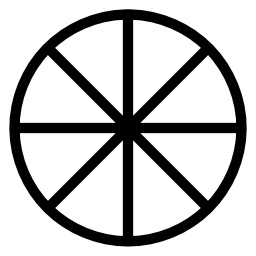
Couper un cercle en 8
Le tracé d'une bissectrice permet de définir deux arcs égaux, et ici de diviser le cercle en 8 parties égales : placer un point entre chaque point déjà placé : on place la pointe du compas sur un des points et l'on trace un arc de cercle à l'extérieur du cercle de base, et l'on fait de même sur le point voisin ; l'intersection des deux arcs définit un point. Puis, on trace à la règle le diamètre passant par ce point-là ; il coupe l'arc de cercle en deux parts égales (bissectrice de l'angle). Ainsi, si le cercle est déjà coupé en 4 parts, on en obtient 8 ; si le cercle est déjà coupé en 12 parts, on en obtient 24. On peut recouper les arcs en 2 par la même méthode, et multiplier ainsi le nombre d'arcs par 2, pour obtenir encore plus d'arcs.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
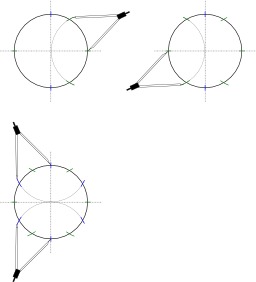
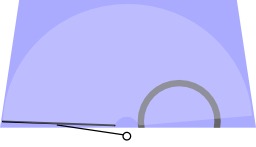
Couper un cercle en douze parties égales
Méthode pour couper un cercle en douze parties égales en trois étapes : Avant de tracer le cercle, on trace les diamètres horizontal et vertical (droites horizontale et verticale passant par le centre) ; ce sont les « traits d'axe du cercle ». Ainsi, lorsque l'on trace le cercle, celui-ci est séparé en 4 quartiers. Pour le séparer en 12 parts égales, on place la pointe du compas sur l'intersection d'un axe et du cercle, tout en gardant un écartement égal au rayon. Puis, on trace les arcs de cercle coupant le cercle. On procède ainsi pour chaque intersection axe-cercle, on obtient au total 12 parts égales.
Photographie, Dix-neuvième siècle, Cercles, Symétrie (art), Londres (GB), Architecture, Dômes, Polychromie architecturale
Dôme polychrome à Londres
Dôme polychrome de la salle centrale des Barry Rooms, dans le musée de la National Gallery de Londres. La National Gallery fut fondée en 1824 et possède une collection de plus de 2300 peintures peintes entre le milieu du XIIIe siècle et 1900. Le bâtiment actuel, situé sur la place de Trafalgar Square, est le troisième à accueillir la collection et fut conçu par William Wilkins entre 1832 et 1838. Les Barry Rooms sont plus tardives, entre 1872 et 1876, et portent le nom de l'architecte qui les a dessinées, Edward Middleton Barry. La coupole surplombe la salle n° 36 et est de style néo-Renaissance.
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres transcendants, Pi (le nombre)
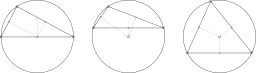
Encadrement de PI par Liu Hui
Représentation de l'encadrement de π par Liu Hui. Si les calculs pratiques peuvent se faire avec une bonne précision en utilisant la valeur 3,14 comme approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416.
Dessins et plans, Géométrie, Cercles, Automobiles -- Essuie-glace, Essuie-glace, Automobiles -- Pare-brise, Technologie
Essuie-glace antagoniste
Essuie-glace à disposition centrée-symétrique ou antagoniste : essuyage opposé.
Dessins et plans, Géométrie, Cercles, Automobiles -- Essuie-glace, Essuie-glace, Automobiles -- Pare-brise, Technologie
Essuie-glace inversé
Essuie glace antagoniste inversé, placé au repos dans l'habillage de chaque pilier du pare-brise.
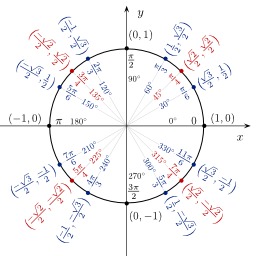
Fonctions trigonométriques dans le cercle unité
Représentation des fonctions trigonométriques dans le cercle unité. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre 0 et π/2. Sur ce cercle sont représentés certains angles communs, et sont indiquées leurs mesures en radians figurant dans l'intervalle [–2π, 2π], soit deux mesures par angle et même trois pour l'angle nul. Notez que les angles positifs sont dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive Ox de l'axe des abscisses coupe le cercle en un point de coordonnées (cos θ, sin θ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
Dessins et plans, Carré, Déclaration, Cercles, Formes (mathématiques), Odysseus, Personnages imaginaires, Cour amoureuse, Explication
Hervé l'ex-carré et Cléandre l'ex-ronde s'expliquent
Hervé l'ex-carré et Cléandre l'ex-ronde s'expliquent, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Surprise, Humour, Cercles, Formes (mathématiques), Transformation, Dessin en noir et blanc, Odysseus, Personnages imaginaires
Hervé l'ex-carré retrouve Cléandre l'ex-ronde
Hervé l'ex-carré retrouve Cléandre l'ex-ronde, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Émotions, Surprise, Cercles, Formes (mathématiques), Dessin en noir et blanc, Odysseus, Personnages imaginaires
Hervé le carré est surpris
Hervé le carré est surpris, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Relations amoureuses, Cercles, Formes (mathématiques), Odysseus, Personnages imaginaires, Âmes soeurs (relations amoureuses)
Hervé le carré et Cléandre la ronde se retrouvent
Hervé le carré et Cléandre la ronde se retrouvent, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Carré, Humour, Cercles, Formes (mathématiques), Transformation, Odysseus, Personnages imaginaires
Hervé le carré s'est arrondi
Hervé le carré s'est arrondi, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Ellipses (mathématiques), Cercles, Sections coniques, Hyperboles (mathématiques), Paraboles (mathématiques)
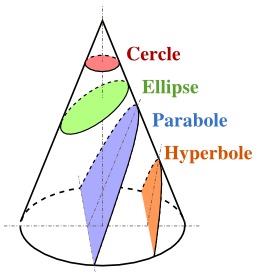
Les quatre sections coniques
Les quatre sections coniques : cercle, ellipse, parabole, hyperbole. Traduction en français Christophe Carina.
Mandala de Sable 03
Premier jour de la réalisation d'un mandala de sable "Pour la paix dans le monde", par trois lamas du temple des Mille Bouddhas, à la Tour de la Liberté de Saint-Dié-des-Vosges, les 11, 12 et 13 avril 2008 : le carré et ses quatre portes, le cercle central.
Mesure d'un tour de roue
Relation entre la rotation d'une roue et l'avance d'un véhicule : longueur de l'arc de cercle. En un tour de roue, on avance d'une longueur correspondant au périmètre.
Dessins et plans, Bleu, Rouge, Vert, Cercles, Mathématiques, Imagerie 3D, Entrelacs (arts décoratifs), Modélisation tridimensionnelle, Noeud borroméen
Noeud borroméen en 3D
Noeud borroméen en 3D : Le nœud borroméen suppose en fait une déformation de ses cercles.
Dessins et plans, Bleu, Rouge, Jaune, Cercles, Mathématiques, Trois (le nombre), Entrelacs (arts décoratifs), Théorie des noeuds, Anneaux topologiques
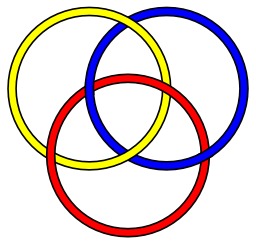
Noeud borroméen en couleur
Nœud borroméen standard. Deux quelconques des cercles sont posés l'un sur l'autre sans se croiser et pourtant l'ensemble des trois cercles est lié par l'un d'entre eux.
Dessins et plans, Cercles, Mathématiques, Trois (le nombre), Entrelacs (arts décoratifs), Théorie des noeuds, Anneaux topologiques
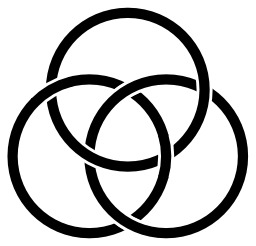
Noeud borroméen en noir et blanc
Nœud borroméen standard. Deux quelconques des cercles sont posés l'un sur l'autre sans se croiser et pourtant l'ensemble des trois cercles est lié par l'un d'entre eux.
Peinture, Néo-impressionnisme (art), Peinture de paysages, Disques, Cercles, Mosaïques, Divisionnisme (art), Robert Delaunay (1885–1941)
Paysage au disque en 1906
Paysage au disque en 1906, par Robert Delaunay (1885–1941). Musée d'Art Moderne de Paris. Entre 1904 et 1906, il réalise une série de portraits et d'autoportraits dans lesquels il applique la technique de la large touche en pavé propre au divisionnisme. Il réalise dans le même temps une série de paysages, toujours en utilisant la méthode divisionniste, dont le célèbre Paysage au disque, peint dans les derniers jours de 1906. Source : http://fr.wikipedia.org/wiki/Robert_Delaunay
Photographie, Urbanisme, Cercles, Égouts, Plaques de regard, Pont-à-Mousson SA, Voisins-le-Bretonneux (Yvelines)
Plaque de regard circulaire
Plaque de regard circulaire d'égout de Pont-à-Mousson à Voisins-le-Bretonneux.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
Puissance d'un point
En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
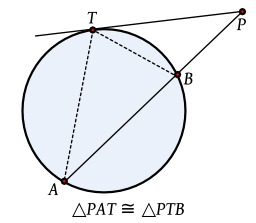
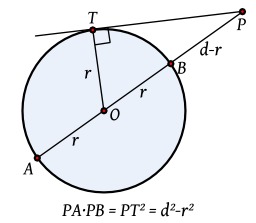
Puissance d'un point
Détermination de la valeur algébrique de la puissance d'un point extérieur à un cercle. En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
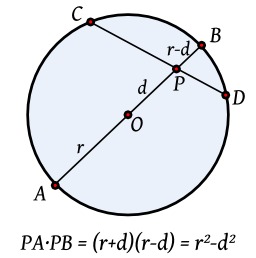
Puissance d'un point intérieur à un cercle
Détermination de la valeur algébrique de la puissance d'un point intérieur à un cercle : PAxPB = (r+d) (r-d).
Quarante-et-un points violets en cercles
Quarante-et-un points violets en trois cercles concentriques autour d'un point central : petit cercle de huit points et deux grands cercles de seize points.
Quart de cercle ayant servi à mesurer la distance à la Lune
Quart de cercle, par Jonathan Sisson, 1742. Monument Historique (Université Claude-Bernard Lyon 1 (Observatoire astronomique de Saint-Genis-Laval), exposé au Musée gallo-romain de Fourvière à Lyon. Utilisé par Jérôme de La Lande pour mesurer la distance entre la Terre et la Lune en 1751.
Peinture, Géométrie, Couleurs, Relief (sculpture), Disques, Cercles, Formes -- Aspect symbolique, Art abstrait, Robert Delaunay (1885-1941), Orphisme (art), Piet Mondrian (1872-1944), Rythme (art)
Relief-disques en 1936
"Relief-disques", 1936, par Robert Delaunay (1885-1941) : gouache et sable sur crayon.
Photographie, Dix-neuvième siècle, Cercles, Symétrie (art), Londres (GB), Architecture, Dômes, Rosaces (vitraux)
Rosace à Londres
Dome et rosace du hall d'entrée de la National Gallery à Londres. Elle fut fondée en 1824 et possède rès de 2 300 tableaux. Le bâtiment actuel à Trafalgar Square est l'oeuvre de l'architecte William Wilkins (1832–38). L'entrée est l'oeuvre de Sir John Taylor (1884–7).