Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Quarante-et-un points violets en cercles
Quarante-et-un points violets en trois cercles concentriques autour d'un point central : petit cercle de huit points et deux grands cercles de seize points.
Quart de cercle ayant servi à mesurer la distance à la Lune
Quart de cercle, par Jonathan Sisson, 1742. Monument Historique (Université Claude-Bernard Lyon 1 (Observatoire astronomique de Saint-Genis-Laval), exposé au Musée gallo-romain de Fourvière à Lyon. Utilisé par Jérôme de La Lande pour mesurer la distance entre la Terre et la Lune en 1751.
Dessins et plans, Géométrie, Douze (le nombre), Cinq (le nombre), Mathématiciens, Polygones, Numération, Un (le nombre), Léonard Euler (1707-1783), Vingt-deux (le nombre)
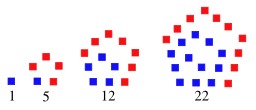
Quatre nombres pentagonaux
Un nombre pentagonal est un nombre figuré qui peut être représenté par un pentagone. Les premiers nombres pentagonaux sont : 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001. Les nombres pentagonaux sont importants dans la théorie des partages d'entiers d'Euler, et ils interviennent par exemple dans son théorème des nombres pentagonaux. Source : http://fr.wikipedia.org/wiki/Nombre_pentagonal
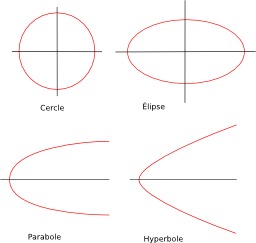
Quatre trajectoires des comètes
les quatre différentes trajectoires de comètes : les coniques forment une famille de courbes planes résultant de l'intersection d'un plan avec un cône de révolution.
Dessins et plans, Géométrie, Cube, Jeux mathématiques, Origami, Pliages en papier, Racines numériques, Racines d'un nombre
Racine cubique de 2 et origami
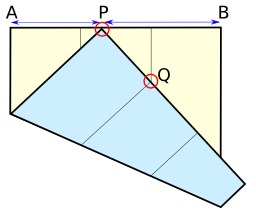
Doubler le volume d'un cube : PB/PA = racine cubique de 2. Comment construire la racine cubique de 2 par pliage d'origami : construction par Peter Messer, Problème 1054, Crux Mathematicorum, Vol. 12, No. 10, 1986, pp. 284-285.
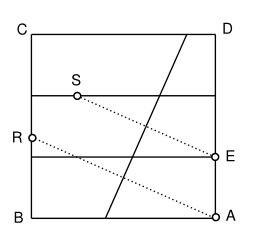
Racine cubique par origami
Construction de la racine cubique de 2 par origami (CR/BR) : On considère un carré ABCD que l'on plie en trois. On effectue un troisième pli de façon que A soit amené sur R et E sur S.
Dessins et plans, Géométrie, Triangulation, Géographie, Réseaux de triangulation, Systèmes d'information géographique
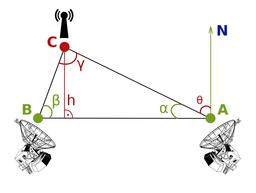
Radiotriangulation
Principe de fonctionnement de la radiotriangulation. Dans le cas d'ondes électromagnétiques (par exemple des ondes radio), la position peut se déterminer avec une antenne directionnelle (c'est-à-dire une antenne ne captant que les ondes venant d'une direction donnée) ; l'orientation pour laquelle le signal est le plus fort donne la direction de l'émetteur, il suffit alors de faire plusieurs relevés pour avoir la position de l'émetteur (radiogoniométrie). Cette méthode était par exemple utilisée durant l'occupation allemande de la France pour détecter les émetteurs radio clandestins.
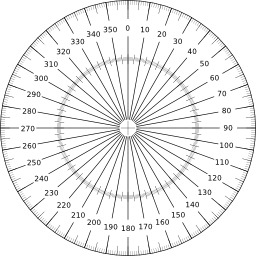
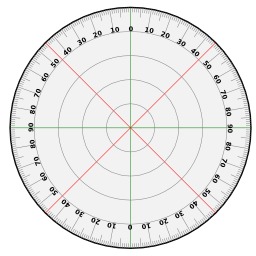
Rapporteur
Schéma d'un rapporteur (à imprimer sur une feuille transparente par exemple) afin de mesurer des angles. Les valeurs sont en degrés. Une attention particulière a été portée à la position des traits afin qu'ils soient bien centrés par rapport à la position de l'angle qu'ils décrivent.
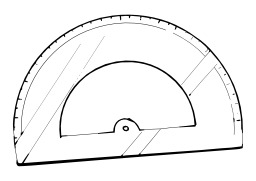
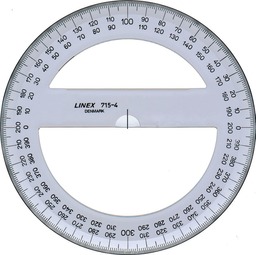
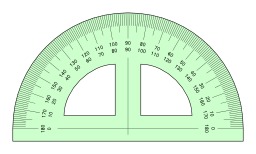
Rapporteur
Un rapporteur (ou rapporteur d'angle) est un outil utilisé en géométrie pour mesurer des angles et pour construire des figures géométriques.
Dessins et plans, Géométrie, Parallèles (géométrie), Thalès, Théorème de, Constructions géométriques, Triangles (géométrie)
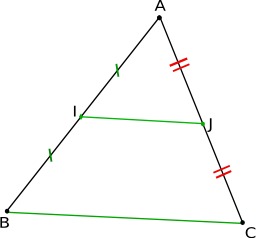
Réciproque du théorème de Thalès
Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès. Si un segment a pour extrémités les milieux de deux côtés d’un triangle, alors il est parallèle au troisième côté, et sa longueur est égale à la moitié de celle de ce troisième côté. Soient I et J les milieux respectifs des segments [AB] et [AC], alors (IJ) // (BC) et IJ = BC ÷ 2.
Peinture, Géométrie, Couleurs, Relief (sculpture), Disques, Cercles, Formes -- Aspect symbolique, Art abstrait, Robert Delaunay (1885-1941), Orphisme (art), Piet Mondrian (1872-1944), Rythme (art)
Relief-disques en 1936
"Relief-disques", 1936, par Robert Delaunay (1885-1941) : gouache et sable sur crayon.
Gravure, Géométrie, Walter Crane (1845-1915), Arts décoratifs -- Motifs du règne végétal, Motifs (art décoratif), Systèmes de quadrillage, Tutoriels, Dessin -- Étude et enseignement, Dessin décoratif -- Motifs végétaux
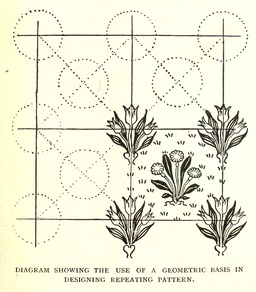
Répétition de motif sur quadrillage
Walter Crane, Line and Form, page 37 : répétition de motif végétal sur quadrillage.
Rotations du tétraèdre
Rotations du tétraèdre : Tout groupe de symétrie dont les éléments ont un point fixe commun, ce qui est vrai pour tous les groupes de symétrie de figures bornées, peut être représenté comme un sous-groupe du groupe orthogonal O(n) en choisissant comme origine un point fixe. Le groupe de symétrie propre est alors un sous-groupe du groupe spécial orthogonal SO(n), c'est pourquoi il est aussi appelé le groupe de rotation de la figure.
Photographie, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Pliages en papier, Mathématiques récréatives, Ferdinand Möbius (1790-1868)
Ruban de Moebius
Ruban de Moebius construit à partir d'une bande de papier, un ruban adhésif retenant les deux bouts. Il est facile de visualiser la bande de Möbius dans l'espace : un modèle simple se réalise en faisant subir une torsion d'un demi-tour à une longue bande de papier, puis en collant les deux extrémités. En topologie, le ruban de Möbius (aussi appelé bande de Möbius ou boucle de Möbius) est une surface compacte dont le bord est homéomorphe à un cercle. Autrement dit, il ne possède qu'une seule face contrairement à un ruban classique qui en possède deux. Elle a la particularité d'être réglée et non-orientable. Source : http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius.
Dessins et plans, Géométrie, Décoration florale, Rubans, Arts décoratifs -- Motifs du règne végétal, Entrelacs, Motifs (art décoratif)
Ruban entrecroisé
Décor géométrique classique d'entrecroisement de ruban : les entrelacs sont une forme d'ornement fondée sur la répétition de motifs de courbes entrelacées, plus ou moins complexes, entrecroisées et enchevêtrées, évoquant les nœuds qu'on peut faire avec des cordes.
Peinture, Géométrie, Couleurs, Cercles, Formes -- Aspect symbolique, Art abstrait, Robert Delaunay (1885-1941), Orphisme (art), Piet Mondrian (1872-1944), Rythme (art)
Rythme en 1932
Vers 1930 se produit un revirement assez difficile à expliquer, qui pousse Delaunay à revenir à l'orphisme, en commençant une série intitulée Rythmes, qui reprend les formes circulaires produites dans les années 1910, de manière nouvelle et plus mature, en s'inspirant notamment du travail de Piet Mondrian, et des artistes regroupés sous le nom d'abstraction-géométrique (dont la plupart reconnaissaient une dette artistique à son égard). Il y montre sa maîtrise dans l'agencement des couleurs, et atteint son but recherché dans les premières année orphiques : l'harmonie picturale. Source : http://fr.wikipedia.org/wiki/Robert_Delaunay
Photographie, Dessins et plans, loup, Lièvres, Bateaux, Grenouilles, Antiquités, Gravure, Peinture, Clip art, Balles et ballons, Amphibiens, Fleurs, Géométrie, Couleurs, Accumulateurs, Piles électriques, Plages, Forêts, Sable, Parasols, Cuisine (pain), Jardinage, Jardins, Réfrigérateurs, Réfrigération et appareils frigorifiques, Bains, Bovins de boucherie, Crustacés, Cuisine -- Appareils et matériel, Nuages, Produits viticoles, feu, Linux (système d'exploitation des ordinateurs), Compas, Salades, Livres illustrés pour enfants, Ombres, laine, Poisson, Plantes des jardins, Confitures, Outillage, Pêches, Cartes à jouer, Mer, Architecture végétale des jardins, Légumes, Potages, Navires à voiles, Découpage (cuisine), Viande, Viande -- Coupe, Étoiles, Cuisine (porc), Saucisses, Enseignes, Tables (meubles), Ongle, Cuisine (aliments naturels), Thé, Bleu, Mouton (viande), soleil, Cuisine (oeufs), Peur chez les animaux, Caricatures et dessins humoristiques, noir, Mécanique, Navires, Triangle, Oeufs, Baies (fruits), Porc, Émotions, Albums à colorier, Nombres cardinaux, Éléments de cuisine, Ustensiles de cuisine, Dinde (viande), Nouvelle-Zélande -- Civilisation, Boissons non alcoolisées, Peur, Pâtisseries, Familles, Fêtes -- Accessoires, Cuisine (fromage), Gelées (confiserie), Maillots de bain, Alimentation, Ciel, Temps -- Systèmes et normes, Oeufs -- Coquilles, Poissons d'eau douce, Parents et enfants, Cuisine (poisson), Véhicules prioritaires, Poulet (viande), Râteaux, Animaux des forêts, Cheminées, Couple -- Psychologie, Espace-temps, Cuisine (sucre), Bains de soleil, Terre, Veaux, Vents, Pyramides, Couple, Graines, Filage à la main, Poissons de mer, Rouge, Aluminium, Vert, Sacs, Membres, Cercle, Navires -- Équipement, Physique, Lumière, Lumière -- Propagation, Joie, Géologie -- Cartes, Poisson rouge, Saumon rouge, Agriculture -- Outillage, Coeur, Art médiéval, Trèfles, Pyramides -- Égypte, Cristaux, Blé, Batteries, Marbre, Fillettes, Caricature, Calcaire, Plantes méditerranéennes, Géométrie euclidienne, Navigation à voile, Cuisine (légumes verts), Sacs en tissu, Pelles, Thalès, Théorème de, Seizième siècle, Dix-neuvième siècle, Dix-septième siècle, Cuivre, Grumes, Albums, Pères, Pères et filles, Sentiers, Maisons individuelles, Pattes, Refus d'obéissance, Jardins médiévaux, Lièvre d'Europe, Méditerranée (région), Cuisine (thym), Aliments crus, Parapente, Vol libre, Dix-huitième siècle, France (Révolution) (1789-1799), Albrecht Dürer (1471-1528), Vinaigre, Poisson fumé, Poisson salé, Auckland (Nouvelle-Zélande), Nouvelle-Zélande (1945-....), Aliments, Cuisine (fruits), Aliments d'origine animale, Aliments fermentés, Cuisine (légumes), Produits de l'oeuf, Boissons alcoolisées, Hérodote (0484?-0420? av. J.-C.), Circulation, Vents -- Vitesse, Métamorphisme (géologie), Savants français, Cuisine (aliments crus), Cuisine (fruits de mer), Cuisine (aliments surgelés), Volaille (viande), Cuisine (poulet), Cuisine (volaille), Produits du blé, Sirops, Sauce à salade, Cuisine (viande), Cuisine (plantes odoriférantes), Crèmes (desserts), Entremets, Poisson surgelé, Agneau (viande), Desserts, Hors-d'oeuvre, Cuisine (baies), Cuisine (vinaigre), Ondes, Cuisine (céréales), Jeux de plage, Conduits d'évacuation de fumées, Fumées, Pull-over, Bronzage, Astérides, Seaux, Serviettes, Chlorure de sodium, Cycle hercynien, Boeuf (viande), Rôtis, Rotissoires, Plats complets, Astacidés, Cuisine (écrevisses), Décapodes (crustacés), Écrevisses, Vinaigrette, Champignons cultivés, Cuisine (champignons), Cuisine (truffes), Truffe du Périgord, Tubéracées, Cassis, Cassissier, Cuisine (cassis), Aliments -- Composition, Blanquette, Cuisine (veau), Veau (viande), Veaux -- Alimentation, Omble de fontaine, Poissonneries, Saumons, Saumons -- Pêche commerciale, Cuisine (semoule), Semoule, Cônes de pin, Pignons (graines), Aliments enrichis, Cuisine (restes), Tourtes, Deux, Jeux de société, Trois, Soupes, Infusions, Lumière, Théorie ondulatoire de la, Cuisson sur réchaud de table, Fondues, Savants allemands, Jumeaux, Interférence (optique), Rhubarbe, Augustin Fresnel (1788 - 1827), Diffraction, Ondes -- Diffraction, Énergie, Photons, Temps, Mesure du, France (Chute des Girondins) ( 30 mai-2 juin 1793), Exécutions capitales et exécuteurs, France (1793), Espace de Minkowski, Relativité (physique), Cônes de lumière, Relativité générale (physique), Architecture égyptienne, Constructions en pierres sèches, Cuisine (rhubarbe), Rhubarbes, Cuisine (boeuf), Cuisines, Aliments -- Consommation, Césium, Horloges à césium, Horloges atomiques, Berne (Suisse), Échelles de temps atomique, Temps (droit international), Johannes Kepler (1571-1630), Des révolutions des orbes célestes - Nicolas Copernic (1473-1543), Héliocentrisme, Énergie éolienne en mer, Portance, Aérodynamique, Relativité restreinte (physique), Muons, Rayons cosmiques, Aquarelle, Le lièvre - Albrecht Dürer (1471-1528), Peintres allemands, Cuisine (plantes aromatiques), Résistance à la chaleur, Thymus (plantes), Abats, Cuisine (abats), Tripes, Aliments -- Réfrigération, Entreposage frigorifique, Frigidaire, Frigo, Danse maorie, Ethnologie -- Nouvelle-Zélande, Linux (logiciels), Rugby, Bayonne (Pyrénées-Atlantiques), Ferias, Aliment, Chevreau (viande), Tacuini sanitatis - al-Muẖtār ibn al-Ḥasan ibn ʿAbdūn ibn Saʿdūn Ibn Buṭlān (10..-1066?), Tangram, Corrosion, Corrosion électrochimique, Assemblages à rivets, Corrosion galvanique, Réactions chimiques -- Mécanismes, Électricité, Symétrie, Constructions géométriques, Génie mécanique, Ressorts et suspension, Ressorts, Volutes, Algues marines, Algues -- Aspect économique, Navires -- Australie, Navires -- Déchets -- Élimination, Navires océanographiques, Navires -- Règlements de sécurité, Sargasses, Mer des, Auteurs arabes, Yuwānīs Ibn Buṭlān (10..-1066?), Jardins -- Aspect symbolique, Famille -- Anthropologie, Famille -- Loisirs, Famille -- Santé et hygiène, Mouton (laine), Quenouilles, Regroupement familial, Veillées, Scènes de la vie quotidienne, Vie quotidienne, Révolution industrielle, Projection cinématographique, Signes et symboles, Carreau, Cartes à jouer, Jeux avec, Pique, Trèfle, Chaleur -- Convection, Dissipateurs thermiques (électronique), Électronique, Acides aminés, Protéines
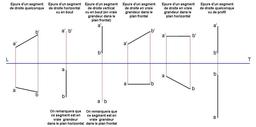
Segments de Droites
Les différentes représentations d'un segment de droite en géométrie descriptive.
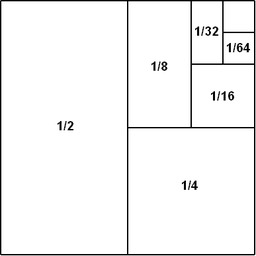
Série géométrique
En mathématiques, la série géométrique est l'un des exemples de série numérique les plus simples qu'on puisse donner. C'est la somme des termes d'une suite géométrique. Intuitivement, une série géométrique est une série avec un ratio constant des termes successifs. Par exemple, la série 1/2 + 1/4 + 1/8 + 1/16 + ... est géométrique, parce que chaque terme successif est obtenu en multipliant le terme précédent par 1/2.
Photographie, Géométrie, Nouvelle-Calédonie, Serres, Paris (France) -- Quartier du Jardin des Plantes, Symétrie (art), Architecture, Serres chaudes
Serre tropicale de la Nouvelle-Calédonie
Composition géométrique à partir de la serre tropicale de la Nouvelle-Calédonie restaurée et réouverte au public en 2010, au Jardin des Plantes de Paris 15 septembre 2010.
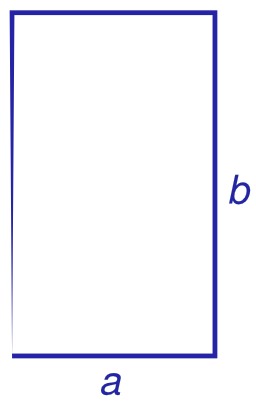
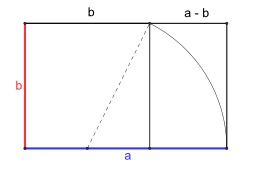
Somme des 2 puissance n.
Représentation géométrique d'une somme algébrique : la somme des 2j si j varie de 0 à n.
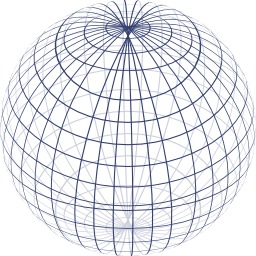
Sphère dans un espace euclidien
En géométrie dans l'espace, une sphère est une surface constituée de tous les points situés à une même distance d'un point appelé centre. La valeur de cette distance au centre est appelée le rayon de la sphère. La géométrie sphérique est la science qui étudie les propriétés des sphères.
Photographie, Géométrie, Boîtes à jeux, Engrenages en plastique, Jeux et récréations, Loisirs créatifs, Spirographes
Spirographe
Instrument de loisir créatif. Le Spirographe, marque déposée par Hasbro, est un instrument de dessin permettant de tracer des figures géométriques, des courbes mathématiques techniquement connues sous le nom d'hypotrochoïdes. Le Spirographe a été inventé par Denys Fisher, qui l'a présenté en 1965 au Salon du jouet de Nuremberg. Les droits de distribution ont été acquis par Kenner, qui l'introduit sur le marché américain en 1966. Le Spirographe est composé de différentes roues et d'anneaux dentés en plastique transparent. Les roues sont les pièces mobiles, et se positionnent dans les anneaux, pièces fixes, de manière à pouvoir y tourner grâce au système d'engrenages.
Photographie, Géométrie, Contribution à la géométrie, Euclide (0323-0285 av. J.-C.), Géométrie euclidienne, Géométrie -- Fondements, Oxford (GB), University of Oxford -- Bibliothèques
Statue d'Euclide
Photographie de la Statue d'Euclide au Musée Universitaire d'Histoire Naturelle à 0xford (Angleterre). En grec ancien Εὐκλείδης Eukleidês (mort à Alexandrie) est un mathématicien de la Grèce antique, auteur des Éléments, qui sont considérés comme l'un des textes fondateurs des mathématiques. La géométrie euclidienne commence avec les Éléments d'Euclide, qui est à la fois une somme des connaissances géométriques de l'époque et une tentative de formalisation mathématique de ces connaissances. Les notions de droite, de plan, de longueur, d'aire y sont exposées et forment le support des cours de géométrie élémentaire. La conception de la géométrie est intimement liée à la vision de l'espace physique ambiant au sens classique du terme.
Photographie, Abeilles mellifères, Géométrie, Miel, Hexagones, Polygones, Agriculture, Produits du rucher, Structures en nids d'abeilles
Structure hexagonale des rayons de miel
Les hexagones réguliers peuvent se juxtaposer les uns les autres sans laisser aucune lacune, comme les carrés et les triangles équilatéraux, et sont ainsi utiles pour construire des pavages. Les cellules des rayons dans une ruche d'abeilles à miel sont hexagonales pour cette raison et parce que cette forme permet une utilisation efficace de l'espace et des matériaux de construction.
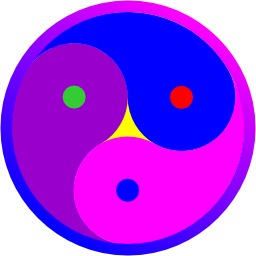
Symbole du Yin-Yang-Yuan
Le tàijí tú : symbole de la dualité yīn-yáng ; ici complémentarité à trois.
Symétrique d'un point par rapport à un point
Construction du symétrique d'un point A par rapport à un point B, à la règle et au compas.
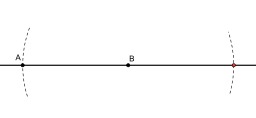
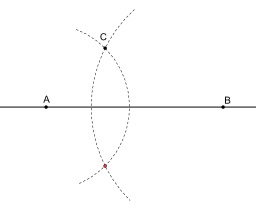
Symétrique d'un point par rapport à une droite
Construction du symétrique d'un point C par rapport à une droite à la règle et au compas : Le symétrique du point C par rapport à la droite (AB) s'obtient en construisant le point d'intersection (différent de C) entre le cercle de centre A passant par C et le cercle de centre B et passant par C. Si le point C est sur la droite (AB), il est son propre symétrique et aucune construction n'est nécessaire.