Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Cube, Carré, Géométrie des nombres, Gnomonique, Abu Bakr Muhammad ibn al-Hasan al- Karaji (....-1019 ?)
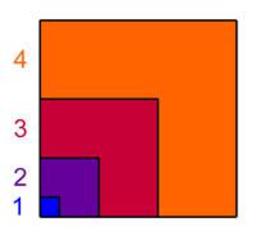
Carré d'un nombre triangulaire
Démonstration géométrique de la formule donnant le carré d'un nombre triangulaire, égal à la somme des premiers cubes parfaits : le carré du nième nombre triangulaire est égal à la somme des n premiers cubes. L'illustration géométrique permet de se convaincre de la véracité de ses propositions. L'aire de la zone orange de la figure est appelée nombre gnomonique. Elle est constituée de deux rectangles de base 4 et de côté le nombre triangulaire d'indice 4, c'est-à-dire 10. Ces deux rectangles se recoupent sur un carré de côté 4, on en déduit que l'aire orange est égale à 5 x 4 x 4 - 4 x 4, ou encore 43. Ce raisonnement est valable sur chaque nombre gnomonique, l'aire du carré de côté le nombre triangulaire d'indice 4 est égal la somme des 4 premiers cubes. De cette démonstration d'Al-Karaji, on déduit la première proposition.
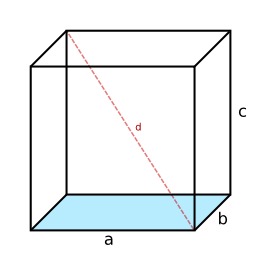
Hexaèdre régulier, le cube
En géométrie des solides, un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube. Le terme hexaèdre vient du grec heksaedros et du bas latin hexahedrum, ce qui justifie la présence de la lettre h dans la traduction anglaise "hexahedron".
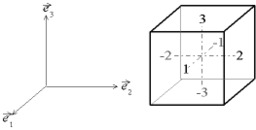
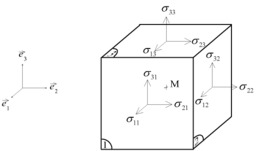
Dessins et plans, Cube, Mécanique, Efforts (mécanique), Contraintes (mécanique), Milieux continus, Mécanique des, Tenseurs, Calcul des
Numérotation des faces du cube
Désignation des faces d'un cube utilisée notamment en mécanique des milieux continus. Le tenseur des contraintes est une représentation utilisée en mécanique des milieux continus pour caractériser l'état de contrainte, c'est-à-dire les efforts intérieurs mis en jeu entre les portions déformées du milieu. Le terme a été introduit par Cauchy vers 1822. Comme les efforts intérieurs sont définis pour chaque surface coupant le milieu (on parle d'ailleurs également d'efforts surfaciques), le tenseur est défini localement, en chaque point du solide. L'état de contrainte du solide est donc représenté par un champ tensoriel. On parle aussi de ce fait de champ de contrainte.
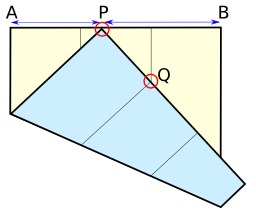
Dessins et plans, Géométrie, Cube, Jeux mathématiques, Origami, Pliages en papier, Racines numériques, Racines d'un nombre
Racine cubique de 2 et origami
Doubler le volume d'un cube : PB/PA = racine cubique de 2. Comment construire la racine cubique de 2 par pliage d'origami : construction par Peter Messer, Problème 1054, Crux Mathematicorum, Vol. 12, No. 10, 1986, pp. 284-285.