Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Antiquités romaines, Octogones, Antiquités byzantines, Sixième siècle, Polygones, Mosaïques, Sousse (Tunisie), Baptistères
Baptistère octogonal de Sousse
Baptistère octogonal recouvert de mosïques de Bekalta (Sousse, Tunisie).
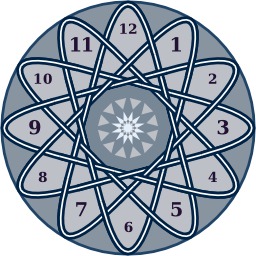
Cadran d'horloge aux 48 ponts
On peut considérer que les nombres entiers de 1 à 12, inscrits sur le cadran de l’horloge, sont les douze nombres des heures, ou les numéros de douze virages le long d’une piste de course. Le long de la boucle, il y a quarante-huit ponts. Chaque ligne droite croise huit autres parties de la piste, en passant alternativement en dessous et au-dessus. Avec ce dessin de nœud, il est facile d’expliquer l’arithmétique modulo 12. Par exemple, si maintenant il est onze heures, dans cinq heures l’aiguille de l’horloge indiquera quatre heures, parce que 11 + 5 = 4 modulo 12. En tournant dans le sens des aiguilles d’une montre, on passe par les termes d’une progression arithmétique de raison +5 ou –7. Cela explique aussi "{12,5}" : une notation de Schläfli qui désigne des dodécagones réguliers étoilés, tous semblables.
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres non-rationnels, Nombres transcendants, Pi (le nombre)
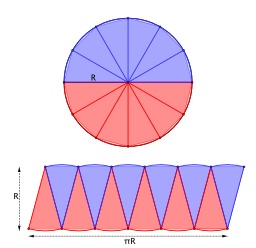
Calcul de l'aire du cercle avec Géogébra
Calcul de l'aire du cercle avec Géogébra : rayon x demi-circonférence. On déduit d’une propriété analogue pour les polygones réguliers que l’aire d’un cercle égale son demi-périmètre multiplié par son rayon. le périmètre du polygone est à peu près 2πr alors qu’en redistribuant les triangles formés on remarque que son aire est à peu près πr2. Pour formaliser le « à peu près » il faudrait faire tendre le nombre de côtés du polygone vers l’infini, ce qui illustre déjà la nature « analytique » de π.
Dessins et plans, Étoiles, Cinq (le nombre), Albums à colorier, Polygones, Coloriages (mathématiques)
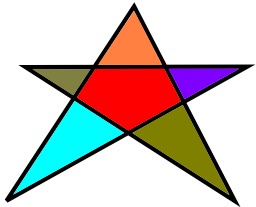
Cinq étoiles à cinq branches
Cinq étoiles à cinq branches utilisables pour l'évaluation ou comme coloriage...
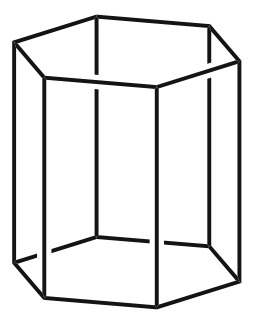
Cinq Poids en fonte
Cinq poids en fonte hexagonaux pour balance : 5 kg, 2 kg, 1 kg, 0,5 kg, 0,2 kg.
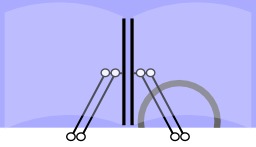
Construction géométrique du drapeau turc
Programme de construction du drapeau turc, croissant de lune et étoiles sur fond rouge.
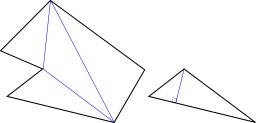
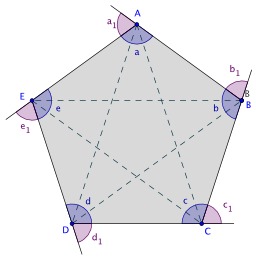
Découpage d'un polygone en triangles
Les triangles ont une importance capitale : en effet, tout polygone — surface délimitée par une ligne brisée fermée — peut se découper en triangles (maillage). Par ailleurs, tout triangle peut se découper en deux triangles rectangles. Ainsi, si l'on sait travailler sur un triangle rectangle, on sait travailler sur tout polygone. Par ailleurs, les triangles rectangles ont des propriétés particulières qui permettent des calculs faciles.
Photographie, Donjons, Douzième siècle, Polygones, Pentagones, Châteaux-forts (France), Grazac (Haute-Loire)
Donjon pentagonal
Vue sur la tour pentagonale datant de la fin du XIIe, début du XIIIe siècle, du château de Carry, à Grazac en Haute-Loire (43).
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres transcendants, Pi (le nombre)
Encadrement de PI par Liu Hui
Représentation de l'encadrement de π par Liu Hui. Si les calculs pratiques peuvent se faire avec une bonne précision en utilisant la valeur 3,14 comme approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416.
Photographie, Étoiles, Cinq (le nombre), Polygones, Entraîneurs sportifs, Gdańsk (Pologne. - région)
Étoile pour entraîneur polonais
Étoile d'argent à cinq branches pour Bogusław Kaczmarek, entraîneur polonais et joueur de football.
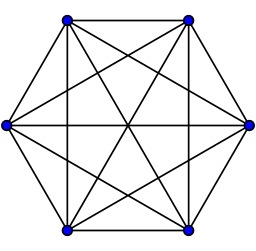
Graphe à six côtés
En théorie des graphes, le graphe complet K_n est l'unique graphe à isomorphisme près possédant n sommets tous reliés deux à deux par une arête, ici 6.
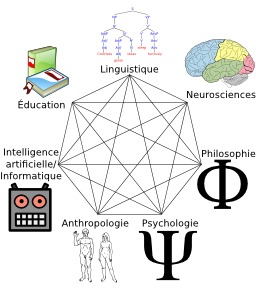
Dessins et plans, Informatique, Anthropologie, Éducation, Intelligence artificielle, Linguistique comparée, Neurosciences, Neurosciences cognitives, Philosophie, Polygones, Psychologie
Heptagramme des sciences cognitives
Heptagramme illustrant les sept disciplines scientifiques des sciences cognitives : linguistique, neurosciences, philosophie, psychologie, anthropologie, intelligence artificielle (informatique), éducation.
Dessins et plans, Carré, Colère, Polygones, Formes (mathématiques), Odysseus, Personnages imaginaires
Hervé le carré s'est transformé en pentagone
Hervé le carré s'est transformé en pentagone, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Hexagone magique (3)
Hexagone magique d'ordre 3 : les nombres de 1 à 19 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 38. En mathématiques, un hexagone magique d'ordre n est un arrangement de nombres formant un gabarit hexagonal centré avec n cellules sur chaque côté. La somme des nombres dans chaque rangée ou dans les trois directions font la même somme. Un hexagone magique normal contient tous les entiers allant de 1 à 3n2 − 3n + 1. Il existe seulement deux arrangements respectant ces conditions, celui d'ordre 1 et celui d'ordre 3. De plus, la solution d'ordre 3 est unique.
Hexagone magique (4)
Hexagone magique (4 cases par côté) : les nombres de 3 à 38 sont placés dans cette grille hexagonale pour que la somme des nombres de chaque rangée soit égale à 111.
Hexagone magique (5)
Hexagone magique d'ordre 5 : les nombres de 6 à 66 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 244.
Hexagone magique (7)
Hexagone magique d'ordre 7 : les nombres de 2 à 128 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 635.
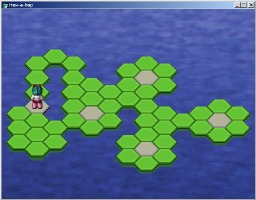
Jeu d'hexagones Hex-a-hop
Jeu de puzzle avec hexagones, créé par Tom Beaumont. Le joueur fait avancer un personnage qui doit détruire tous les hexagones verts en sautant dessus. Les hexagones gris sont des point sûrs, sur lesquels il est possible de passer indéfiniment.
Photographie, Antiquités grecques, Vents, Octogones, Mythologie grecque, Polygones, Huit (le nombre), Architectes grecs, Athènes (Grèce) -- Tour des Vents
La tour octogonale des vents à Athènes
Tour des vents à Athènes, utilisée comme calendrier solaire et astrologique par Andronikos of Kyrrhos (d'après Vitruve). Les huit vents sont : Borée (nord, homme barbu, les cheveux en broussaille, vêtu d'une robe flottante formée de tourbillons et tenant une conque dans ses mains) ; Cécias (nord-est, représenté comme un homme barbu tenant et déversant un bouclier plein de grêlons) ; Apéliote (est, jeune homme portant une robe remplie de fruits et de céréales) ; Euros (sud-est, homme âgé et barbu, drapé dans une lourde robe pour se protéger des éléments) ; Notos (sud, homme déversant une urne et provoquant une averse) ; Lips (sud-ouest, jeune homme accroché à la poupe d'un navire, promettant des vents favorables) ; Zéphyr (ouest, jeune homme imberbe dispersant dans les airs des fleurs de son manteau) ; Sciron (nord-ouest, homme barbu semant des cendres incandescentes d'un vase de bronze, pour signifier le début de l'hiver).
Photographie, Étoiles, Dix-huitième siècle, Polygones, Architecture, Pentagones, Ancône (Italie), Lazarets, Léproseries
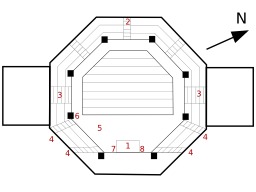
Lazaret pentagonal d'Ancône
Lazaret pentagonal d'Ancône en Italie. Le Lazaret (Lazzaretto or Mole Vanvitelliana) a été conçu par Luigi Vanvitelli en 1732 ; c'est un bâtiment pentagonal formant une île entourée de fossés de plus de 2 000 m2 de superficie. Il a servi de quarantaine pour protéger la défense militaire de maladies contagieuses qui arriveraient depuis la mer. Plus tard, il a été aussi servi d’hôpital militaire et sert actuellement lors de manifestations culturelles et d'un festival du cinéma d'été.
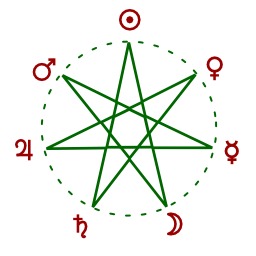
Les sept jours de la semaine
Heptagramme représentant les sept jours de la semaine. Chaque jour est représenté par le signe astrologique de l'objet céleste associé au nom latin. Liste des symboles : Soleil, Vénus, Mercure, croissant de Lune, Saturne, Jupiter, Mars. Pour les retrouver dans l'ordre des jours de la semaine, suivre les segments sans relever le doigt : dimanche, lundi (lunes), mardi (martes), mercredi (Mercure), jeudi (Jupiter), vendredi (Venus), samedi (Saturne). Source : http://www.symbols.com/encyclopedia/29/2916.html
Dessins et plans, Géométrie, Lune, Étoiles, Cinq (le nombre), Triangle, Polygones, Quatre (le nombre), Turquie
Lune et quatre étoiles turques
Reprise géométrique d'Ay yildiz, le drapeau de la Turquie : lune décroissante et étoile à cinq banches
Monument des étoiles
Monument des étoiles à Dinod (Bhiwani, Haryana) en Inde. (étoile à cinq branches)
Photographie, Dessins et plans, Géométrie, Carré, rectangle, rectangles, Angles, Parallèles (géométrie), Parallélogrammes, Polygones, Tablettes d'argile cunéiformes, Pentagones, Diagonales, Racine carrée de deux, Losanges, Quadrilatères, Trapèzes, Aires (surfaces), Aires (surfaces) -- Mesure
Parallélograme
Exemple de parallélogramme. Un parallélogramme, en géométrie, est un quadrilatère dont les côtés opposés sont parallèles deux à deux
Photographie, Art islamique, Charges, Chiens, Polygones, Ivoires, Ivoires médiévaux, Art fāṭimide, Égypte (Fatimides) (969-1171), Panneaux de revêtement
Plaque en ivoire gravée
Plaque pentagonale en ivoire gravée, représentant un homme chargé d'un baluchon, courant avec son chien. Période fatimide (909-1171).
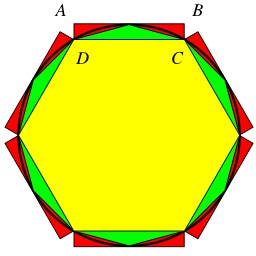
Pliage de pentagone
Pentagone obtenu en faisant un nœud avec un ruban de papier rectangulaire replié sur lui-même. Il est possible de construire un pentagone régulier à la règle et au compas. Une méthode par pliage simple permet de faire un pentagone. Il suffit de prendre une bande de papier suffisamment longue et de faire une boucle, puis de passer un bout dans la boucle et enfin serrer en ajustant.
Dessins et plans, Géométrie, Douze (le nombre), Cinq (le nombre), Mathématiciens, Polygones, Numération, Un (le nombre), Léonard Euler (1707-1783), Vingt-deux (le nombre)
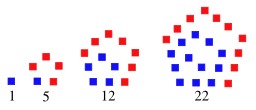
Quatre nombres pentagonaux
Un nombre pentagonal est un nombre figuré qui peut être représenté par un pentagone. Les premiers nombres pentagonaux sont : 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001. Les nombres pentagonaux sont importants dans la théorie des partages d'entiers d'Euler, et ils interviennent par exemple dans son théorème des nombres pentagonaux. Source : http://fr.wikipedia.org/wiki/Nombre_pentagonal
Photographie, Abeilles mellifères, Géométrie, Miel, Hexagones, Polygones, Agriculture, Produits du rucher, Structures en nids d'abeilles
Structure hexagonale des rayons de miel
Les hexagones réguliers peuvent se juxtaposer les uns les autres sans laisser aucune lacune, comme les carrés et les triangles équilatéraux, et sont ainsi utiles pour construire des pavages. Les cellules des rayons dans une ruche d'abeilles à miel sont hexagonales pour cette raison et parce que cette forme permet une utilisation efficace de l'espace et des matériaux de construction.