Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Rubans, Bouteilles, Mathématiciens, Ferdinand Möbius (1790-1868), Felix Klein (1849-1925)
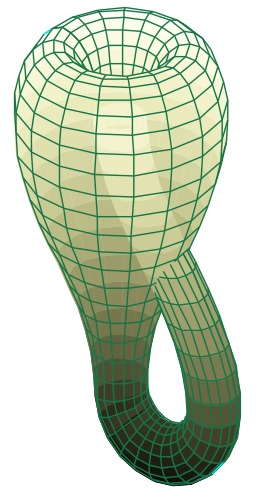
Bouteille de Klein
Vue de la bouteille de Klein dans un espace à trois dimensions. En mathématiques, la bouteille de Klein (prononcé kla.in) est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle il n'est pas possible de définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein (1849-1925). Elle est étroitement liée au ruban de Möbius.
Photographie, Fruits, Chocolat, Rubans, Cadeaux, Papier cadeau, Paniers, Corbeilles, Cadeaux -- Emballage, Noeuds décoratifs, Noeuds ornementaux
Corbeille de fruits
Corbeille de fruits et de chocolat emballée dans un papier cadeau transparent avec noeud blanc.
Photographie, Sapeurs-pompiers -- France, Rubans, Véhicules prioritaires, Dispositifs de sécurité, Échelle mobile, Incendies -- Extinction -- Appareils et matériel, Rouge
Échelle de pompiers
Photo d'un camion de pompiers, grande échelle dépliée, adossée à un mur d'habitation ; un périmètre de sécurité a été aménagé dans la rue.
Peinture, Marguerites, Vêtements, Peintres français, Chemises, Jupes, Rubans, Vert, Pâquerettes, Fillettes, Dix-neuvième siècle, William Bouguereau (1825-1905), Tabliers
La couronne de paquerettes
Fillette assise tressant une couronne de paquerettes, 1874, par William Bouguereau (1825-1905) : elle porte une jupe, un tablier et une chemise blanche, ainsi qu'un ruban dans les cheveux du même vert que son tablier.
Photographie, Rubans, Nains, Sourds, Aveugles, Wrocław (Pologne), Breslau (Pologne), Handicapés auditifs, Handicapés visuels, Inaugurations, Sourds-aveugles, Figurines de bronze
Le nain sourd et le nain aveugle
Inauguration de deux nouveaux nains, un mal-voyant et un mal-entendant, en 2008 à Wrocław (Pologne).
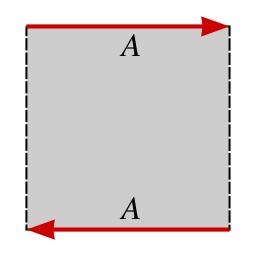
Dessins et plans, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Collages (art)
Montage d'un ruban de Möbius
Schéma de montage d'un ruban de Möbius : recoller les deux flèches en respectant le sens.
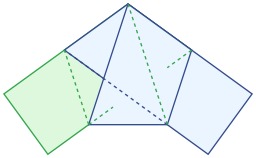
Pliage de pentagone
Pentagone obtenu en faisant un nœud avec un ruban de papier rectangulaire replié sur lui-même. Il est possible de construire un pentagone régulier à la règle et au compas. Une méthode par pliage simple permet de faire un pentagone. Il suffit de prendre une bande de papier suffisamment longue et de faire une boucle, puis de passer un bout dans la boucle et enfin serrer en ajustant.
Peinture, Vêtements, Rubans, Couture, Soie, Robes (vêtements pour femmes), Femmes, Teinture -- Soie, Femmes -- Costume, Mode, Mousseline (tissu)
Robe de diner
"Robe en mousseline de soie blanche, bordée de larges rubans satinés, peints de roses pâles. Corsage et jupe drapés, manches faites de rubans." Photograph in ''Les Modes : Revue mensuelle illustrée des arts décoratifs appliqués à la femme''. Robe de dîner par Redfern 1908
Photographie, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Pliages en papier, Mathématiques récréatives, Ferdinand Möbius (1790-1868)
Ruban de Moebius
Ruban de Moebius construit à partir d'une bande de papier, un ruban adhésif retenant les deux bouts. Il est facile de visualiser la bande de Möbius dans l'espace : un modèle simple se réalise en faisant subir une torsion d'un demi-tour à une longue bande de papier, puis en collant les deux extrémités. En topologie, le ruban de Möbius (aussi appelé bande de Möbius ou boucle de Möbius) est une surface compacte dont le bord est homéomorphe à un cercle. Autrement dit, il ne possède qu'une seule face contrairement à un ruban classique qui en possède deux. Elle a la particularité d'être réglée et non-orientable. Source : http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius.
Dessins et plans, Géométrie, Décoration florale, Rubans, Arts décoratifs -- Motifs du règne végétal, Entrelacs, Motifs (art décoratif)
Ruban entrecroisé
Décor géométrique classique d'entrecroisement de ruban : les entrelacs sont une forme d'ornement fondée sur la répétition de motifs de courbes entrelacées, plus ou moins complexes, entrecroisées et enchevêtrées, évoquant les nœuds qu'on peut faire avec des cordes.