Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Nombre triangulaire
Le 28 est le septième nombre triangulaire ou encore le nombre triangulaire d'indice 7 : en arithmétique, un nombre triangulaire est un cas particulier de nombre figuré. Il correspond à un nombre entier positif égal au nombre de pastilles dans un triangle construit à la manière de cette figure. Source : p. 320, Die Gartenlaube (1887), Ernst Keil's Nachfolger.
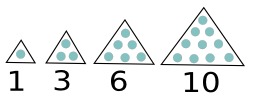
Nombres triangulaires
Représentation graphique des premiers nombres triangulaires : la représentation figurée permet un calcul pour les premières valeurs. Une définition formelle s'obtient par récurrence : le nombre triangulaire d'indice 1 est égal à 1, et un nombre triangulaire est égal à son prédécesseur additionné de son indice. Les premiers nombres triangulaires sont : 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ... Il existe différentes manières de calculer le nombre triangulaire d'indice n, l'une d'elles est graphique et s'obtient par un raisonnement d'arithmétique géométrique.
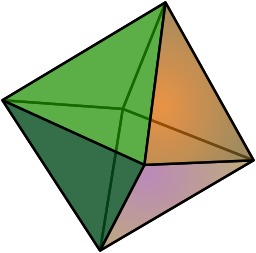
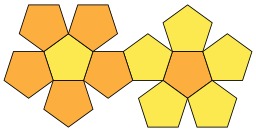
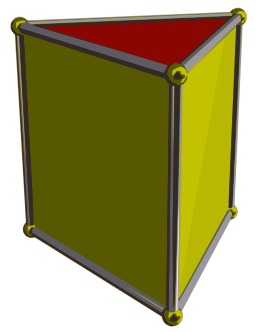
Octaèdre régulier
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces, notamment l'octaèdre régulier. Un octaèdre dont toutes les faces sont triangulaires, possède alors douze arêtes et six sommets.
Dessins et plans, Géométrie, Lune, Berlin (Allemagne), Astronomes, Parallaxe, Trigonométrie, Jérôme de La Lande (1732-1807), Le Cap (Afrique du Sud), Nicolas-Louis de La Caille (1713-1762)
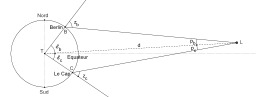
Parallaxe de la Lune entre Berlin et Le Cap
Illustration du calcul de la parallaxe de la lune entre Berlin et Le Cap, par Lalande et Lacaille (étape 2). Durant l'année 1751, Jérôme de La Lande situé à Berlin et Nicolas-Louis de La Caille situé au Cap entreprennent une série de mesures synchrones qui permettront de déterminer avec une relative précision la parallaxe de la Lune. Ils mesurent à des jours fixés la hauteur de la Lune quand celle-ci passe au méridien. La différence de longitude entre ces deux villes est assez faible pour que l'on puisse supposer que la position de la Lune n'a pas significativement changé. La réunion de ces deux mesures permet de déterminer la parallaxe lunaire au moment de l'observation. Lalande trouve ainsi une parallaxe moyenne de 57 minutes et 26 secondes. Le principe en est expliqué par Lalande dans son traité d'astronomie.
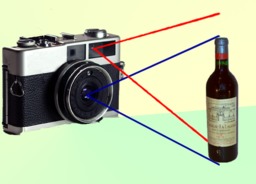
Parallaxe de visée
La parallaxe de visée est la différence de cadrage entre l’image donnée par un viseur et l’image passant dans l’objectif d’un appareil photographique. Un appareil photographique bi-objectif est un appareil dans lequel la visée est effectuée à travers un objectif situé au-dessus de l’objectif de prise de vue. L’imprécision due à la parallaxe n’existe bien sûr pas avec un appareil photographique reflex mono-objectif (dont la visée se fait à travers la lentille de prise de vue grâce à un miroir).
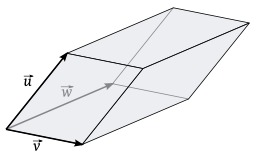
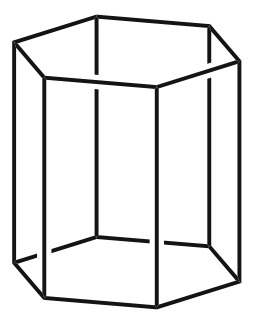
Parallélépipède déterminé par trois vecteurs
Parallélépipède déterminé par trois vecteurs. En géométrie dans l'espace, les parallélépipèdes sont des hexaèdres dont les faces sont parallèles deux à deux.
Photographie, Dessins et plans, Géométrie, Carré, rectangle, rectangles, Angles, Parallèles (géométrie), Parallélogrammes, Polygones, Tablettes d'argile cunéiformes, Pentagones, Diagonales, Racine carrée de deux, Losanges, Quadrilatères, Trapèzes, Aires (surfaces), Aires (surfaces) -- Mesure
Parallélograme
Exemple de parallélogramme. Un parallélogramme, en géométrie, est un quadrilatère dont les côtés opposés sont parallèles deux à deux
Dessins et plans, Géométrie, Jeux mathématiques, Pavages (mathématiques), Mathématiciens, Tuiles, Divertissements mathématiques
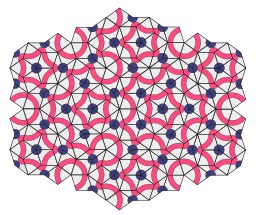
Pavage de Penrose avec tuiles apériodiques
Pavage de Penrose réalisé avec deux tuiles apériodiques. Roger Penrose est un mathématicien anglais. Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement. Plus généralement toute portion finie du pavage, aussi grande soit-elle, se répète infiniment dans le pavage. Les pavages de Penrose ne seraient restés qu'un joli divertissement mathématique si n'avaient été découverts, en 1984, des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux. Les pavages non périodiques, en particulier ceux de Penrose, s'avérèrent alors un modèle plausible de ces étranges matériaux. Cette découverte illustra à nouveau ce que Roger Penrose lui-même avait déjà remarqué en 1973, à propos d’un sujet de relativité générale : « On ne sait jamais vraiment quand on perd son temps ». Source : http://fr.wikipedia.org/wiki/Pavage_de_Penrose.
Photographie, Géométrie, Vitraux, Artistes italiens, Art contemporain, Carlo Roccella (né en 1956), Contribution au vitrail, Art abstrait
Peinture sur verre de vitrail contemporain
Peinture sur verre de vitrail contemporain, par Carlo Roccella (né en 1956), artiste italien dont l'atelier est à Béziers depuis 2011. Source : http://fr.wikipedia.org/wiki/Carlo_Roccella
Dessins et plans, Géométrie, Mécanique, Dessin industriel, Ingénieurs militaires, Orthogonalisation, Méthodes d', Perspective cavalière
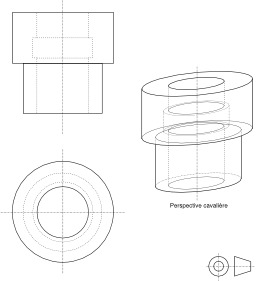
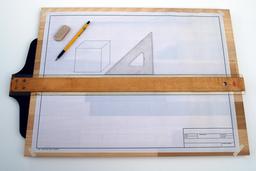
Perspective cavalière
La perspective cavalière est introduite au XVIè siècle par les ingénieurs militaires. Elle permet d'obtenir une image plane la plus fidèle possible d'un objet dans l'espace et d'étudier ses propriétés métriques (angles, orthogonalité, longueur). Elle montre l'agencement des parties d'un objet : c'est pourquoi elle est utilisée pour le dessin industriel et la mécanique.
Perspective cavalière à 90°
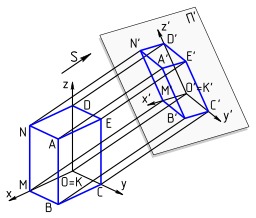
Comparaison entre les projections orthogonales sur les plans contenant les axes (géométrie descriptive) et la perspective cavalière : report des coordonnées. Pour effectuer une représentation en perspective cavalière, il faut choisir différents paramètres : 1) un plan frontal : un segment contenu dans ce plan, ou dans un plan parallèle, est représenté en vraie grandeur ; 2) un angle de fuite : les perpendiculaires au plan frontal, appelées fuyantes sont représentées dans cette direction ; 3) un coefficient de réduction : les longueurs représentées dans la direction de fuite sont multipliées par ce coefficient de réduction. De plus, l'alignement des points, le parallélisme des droites le rapport des longueurs de deux segments parallèles, et donc les milieux, sont conservés. En revanche, les longueurs, les aires, et les angles ne sont pas conservés dans les plans non frontaux. Les éléments cachés par les faces supposées opaques sont représentés en pointillés; les éléments visibles par l'observateur sont représentés en traits pleins.
Gravure, Géométrie, Dix-huitième siècle, Savants, Savants anglais, Perspective cavalière, Axonométrie, Fortifications
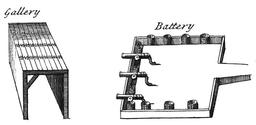
Perspective cavalière en dessins de fortifications
Source : Ephraim Chambers (1680–1740), "Cyclopaedia, or an Universal Dictionary of Arts and Sciences" 1728. La perspective cavalière est une manière de représenter en deux dimensions des objets en volume. Cette représentation ne présente pas de point de fuite : la taille des objets ne diminue pas lorsqu'ils s'éloignent. C'est une forme particulière de perspective axonométrique, où l'on situe les points grâce à leurs coordonnées dans un repère formé de trois axes. Dans cette perspective, deux des axes sont orthogonaux et ont un facteur de report de 1. Le troisième axe est incliné, en général de 30 ou 45° par rapport à l'horizontale, appelé « angle de fuite », et a un facteur de report inférieur à 1, en général. Cette perspective ne prétend pas donner l'illusion de ce qui peut être vu, mais simplement donner une information sur la notion de profondeur. Simple à réaliser, c'est une perspective naïve qui peut traduire un manque de « vision dans l'espace ». Trop souvent utilisée dans les dessins à main levée, elle est malgré tout à déconseiller par son ambiguïté de représentation : un objet éloigné d'un autre peut sembler être plutôt au-dessus ou au-dessous. Cette représentation était utilisée initialement pour la conception des fortifications militaires. Le « cavalier » est un promontoire de terre situé en arrière des fortifications et qui permet de voir par-dessus, et donc de voir les assaillants. La perspective cavalière était donc la vue que l'on avait du haut du cavalier (les anglais utilisent parfois le terme de « high view point », en français « point de vue de haut »). Certains avancent également que c'est la vue qu'a un cavalier du haut de son cheval.
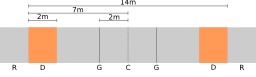
Piste d'escrime
Piste d'escrime : C) ligne centrale ; G) ligne de mise en garde ; D) zone des deux mètres ; R) zone de recul (sortie de piste). Une piste d'escrime mesure 14 mètres de long sur 1,5 à 2 mètres de large. Elle est marquée par des lignes perpendiculaires en divers endroits (centre de la piste, ligne de mise en garde, et limite arrière, outre les 2 derniers mètres doivent être clairement identifiés). Si un tireur sort par l'un des bords latéraux de la piste, l'action est interrompue et les tireurs se remettent en garde en ayant néanmoins fait avancer d'un mètre l'adversaire du tireur qui est sorti ; ce dernier devant donc reculer et se remettre à distance. Si un tireur sort des deux pieds par le bout arrière de la piste, il est considéré comme touché. Source : http://fr.wikipedia.org/wiki/Escrime
Photographie, Géométrie, Étoiles, Histoire, Fortifications -- France, Plans-reliefs, France -- 1643-1715 (Louis XIV), Lille (Nord) -- Citadelle, Sébastien Le Prestre de Vauban (1633-1707)
Plan de la citadelle de Lille de Vauban
Plan de la citadelle de Lille. ''Louis Le Grand la voulut, Vauban la dessina, Simon Vollant l'édifia''.
Dessins et plans, Géométrie, Anatomie humaine, Biologie humaine, Terminologie, Vocabulaire fondamental
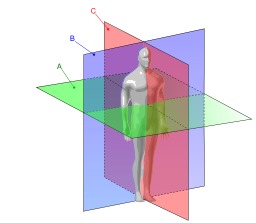
Plans de direction de l'anatomie de l'homme
Plans de direction de l'anatomie de l'homme : A) coupe transversale (en vert) ; B) coupe sagittale (en bleu) ; C) coupe frontale (en rouge).
Photographie, Géométrie, Carré, Triangle, Urbanisme, Isostasie, Égouts, Plaques de regard, Structures hyperstatiques
Plaque d'égout isostatique
Plaque d'égout isostatique : une plaque d'égout classique n'est jamais parfaitement plane ni l'appui sur lequel elle repose. Il en résulte un bruit de basculement, métal sur métal, chaque fois qu'on marche dessus ou, plus énervant encore, lorsqu'une roue de voiture la traverse. La solution a consisté à supprimer cet appui hyperstatique et à le remplacer par un appui en trois points : deux demi-plaques triangulaires jumelles dessinent un carré coupé en diagonale. Ces demi-plaques sont articulées selon deux côtés opposés du carré, le troisième appui étant constitué par la pointe que l'on relève pour accéder au regard. Source : http://fr.wikipedia.org/wiki/Plaque_d%27%C3%A9gout
Dessins et plans, Géométrie, Panneaux solaires, Cartes géographiques, Origami, Pliages en papier, Astrophysiciens
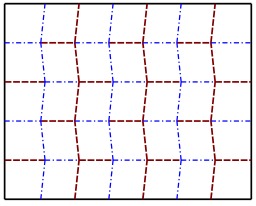
Pliage d'origami de Miura-Ori
Grille de pliage d'origami de Miura-ori, inventée par l'astrophysicien Koryo Miura et utilisée pour les panneaux solaires et les cartes géographiques (http://www.miura-ori.com).
Dessins et plans, Géométrie, Jeux mathématiques, Oursins, Origami, Pliages en papier, Napperons individuels, Sets de table
Pliage de napperon en origami
Pliage de napperon en origami, à partir des recherches de J. Lang de pliages pour l'oursin. Source : http://en.wikipedia.org/wiki/Napkin_folding_problem
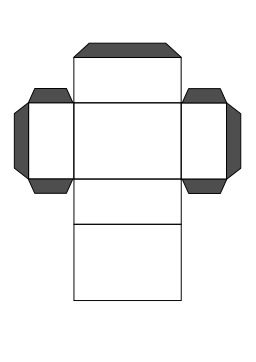
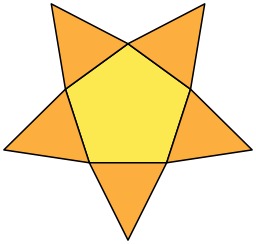
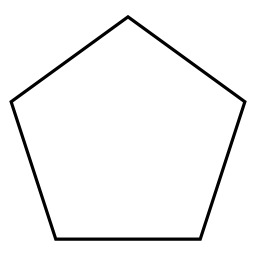
Pliage de pentagone
Pentagone obtenu en faisant un nœud avec un ruban de papier rectangulaire replié sur lui-même. Il est possible de construire un pentagone régulier à la règle et au compas. Une méthode par pliage simple permet de faire un pentagone. Il suffit de prendre une bande de papier suffisamment longue et de faire une boucle, puis de passer un bout dans la boucle et enfin serrer en ajustant.
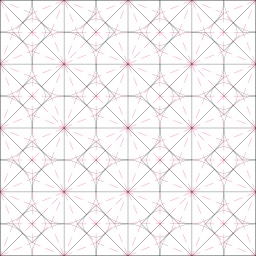
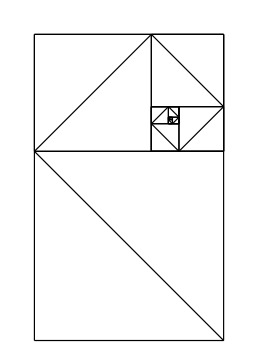
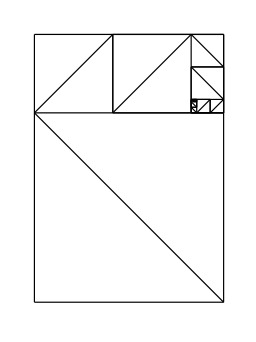
Pliage fractal 02 en Origami
Pliage fractal 02 en origami : dans le rectangle restant, aux mêmes proportions que le premier, il est encore possible de retirer deux carrés, puis de recommencer, théoriquement jusqu'à l'infini.
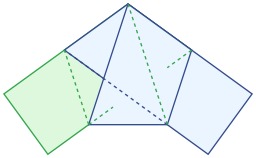
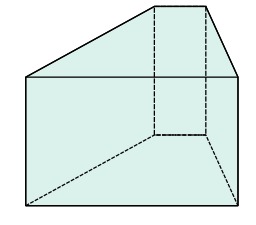
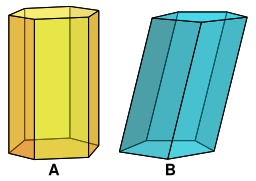
Prisme droit et prisme oblique
Prisme droit (A, jaune) et prisme oblique (B, bleu). Lorsque le plan est perpendiculaire à la droite génératrice (d), le prisme est appelé prisme droit. Lorsque le prisme est droit, les faces latérales sont des rectangles.
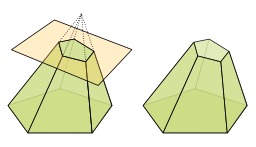
Projection axonométrique
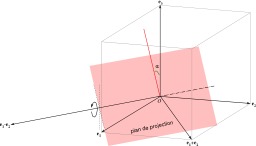
Principe de l'axonométrie : le pavé se projette sur le plan Π' selon la direction S, l'image obtenue est une perspective axonométrique du pavé.
Projection orthogonale
La projection orthogonale est un type de perspective très utilisée en dessin (géométrie descriptive), et en infographie : la génération des figures est simple, par contre, on ne peut pas représenter l'éloignement (la taille des objets ne varie pas avec la distance). De manière plus générale, en algèbre linéaire, une projection orthogonale est un projecteur tel que les deux sous-espaces sont orthogonaux. La projection orthogonale permet de résoudre le problème de la plus courte distance d'un point à une droite, d'un point à un plan, ou plus généralement d'un point à un sous-espace affine d'un espace euclidien d'autre part. On peut alors utiliser ce concept pour résoudre des problèmes de type «moindres carrés». L'idée générale, basée sur le théorème de Pythagore, est que le problème de plus courte distance se ramène à une propriété d'orthogonalité.
Projection orthogonale dimétrique
Projection dimétrique : le plan de projection tourne autour de la deuxième bissectrice du plan (Oxy), c'est-à-dire autour du vecteur vec{e}_1 + vec{e}_2. . Choisissons k1 = k2 ; les projections des axes x et y sont symétriques par rapport à la verticale. Cette situation est un cas particulier de la projection orthogonale avec ω = 45 °.
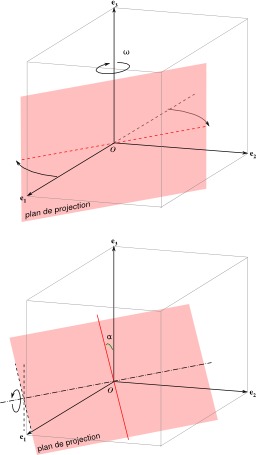
Projection orthogonale et rotation
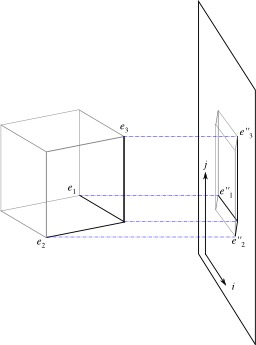
Angles de rotation du plan de projection afin d'obtenir une perspective par projection orthogonale avec l'axe des ''z'' vertical. On peut décrire le plan de projection par des rotations transformant un plan donné, par exemple le plan (Oxz). Si l'on s'impose que la projection de vec{e}_3 reste verticale, alors on voit que le plan de projection peut s'obtenir par deux rotations, par exemple : 1) une rotation autour de l'axe (Ox) ; puis une rotation autour de la projection de (Oz) sur le plan. 2) On peut aussi procéder dans « l'ordre inverse » : une rotation autour de (Oz) ; puis une rotation autour de la trace du plan (Oxy) sur le plan de projection.
Gravure, Géométrie, Paris (France) -- Palais des Tuileries, Monuments historiques, Axonométrie, Projection axonométrique, Jacques Androuet Du Cerceau (1510?-1585?), Tuileries (Paris, France), Palais des
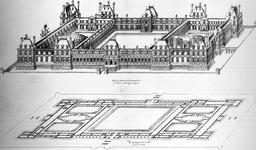
Projet du château des Tuileries
Dessin en perspective cavalière du projet de château des Tuileries, en 1578-1579, par Jacques Androuet du Cerceau (1510-1584). Les premières représentations en perspective parallèle apparaissent au XVIe siècle sous la plume d'Androuet du Cerceau qui construit des perspectives cavalières empiriques. Jacques Ier Androuet du Cerceau (1510 ? -1585 ?), est un graveur et architecte français de la seconde moitié du XVIe siècle, célèbre pour ses gravures d'architecture et ses publications : il a publié quelques livres contenant des modèles très importants d'ornements et des travaux sur l'architecture, qui auront une forte influence sur les architectes français du XVIIe siècle et au-delà. Son ouvrage le plus connu reste "Les plus excellents bastiments de France" où il décrit avec minutie et talent les réalisations majeures des architectes de son temps. Ses dessins, plans, élévations, détails et commentaires constituent un témoignage unique sur des constructions dont beaucoup n'existent plus aujourd'hui, ou ont été très largement remodelées par les siècles.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
Puissance d'un point
En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
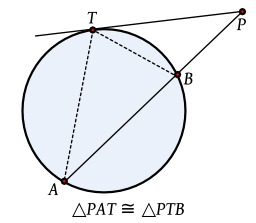
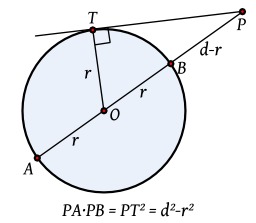
Puissance d'un point
Détermination de la valeur algébrique de la puissance d'un point extérieur à un cercle. En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
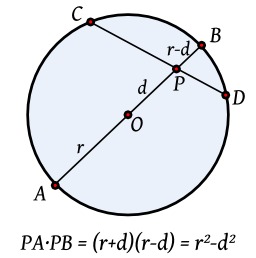
Puissance d'un point intérieur à un cercle
Détermination de la valeur algébrique de la puissance d'un point intérieur à un cercle : PAxPB = (r+d) (r-d).