Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Gravure, Géométrie, paris, Dix-neuvième siècle, Villes -- Plans, Élections, Cartographie statistique, Statistiques
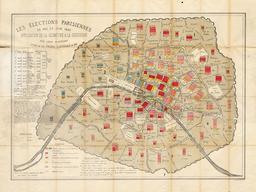
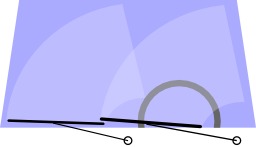
Élections parisiennes de mai et juin 1869
Les élections parisiennes de mai et juin 1869, application de la géométrie à la statistique, par Léon Montigny
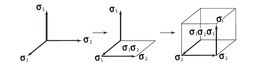
Éléments de l'algèbre géométrique
Interprétation des divers éléments d'une algèbre géométrique issue de l'espace vectoriel Euclidien 3D.
Dessins et plans, Géométrie, Jeux mathématiques, Jeux de logique, Mathématiciens, Devinettes et énigmes, Casse-tête logique, Énigmes mathématiques, Henry Dudeney (1857-1930)
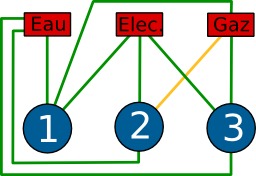
Enigme des 3 maisons
Enigme des trois maisons : Une solution généralement non admise dans l'énigme des trois maisons puisque les canalisations de gaz et d'électricité se croisent. Enigme posée en 1917 par Henry Dudeney (1857-1930) en ces termes : "Un lotissement de trois maisons doit être équipé d'eau, de gaz et d'électricité. La règlementation interdit de croiser les canalisations pour des raisons de sécurité. Comment faut-il faire ?"
Photographie, Géométrie, Décorations et ornements architecturaux, Entrelacs (arts décoratifs), Florence (Italie) -- Palazzo Rucellai
Entrelac italien au quinzième siècle
Entrelac au "petit temple du Saint-Sépulcre" Rucellai à Florence, datant du XVème siècle.
Photographie, Géométrie, Outils, Outils à bois, Objets en acier, Menuisiers, Travail du bois -- Outillage, Equerre
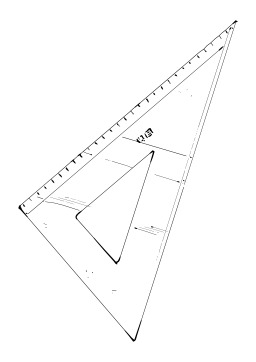
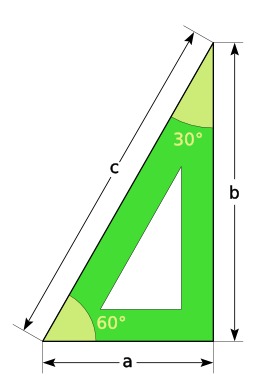
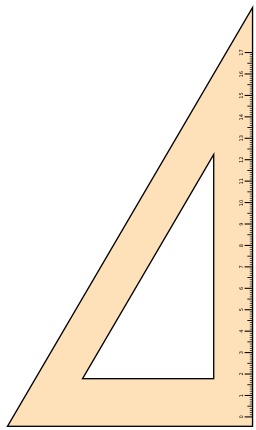
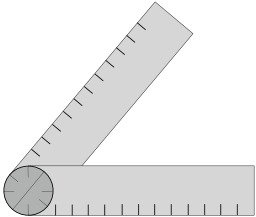
Équerre de menuisier
Équerre métallique avec graduations de menuisier. Une équerre est un instrument formé de deux pièces ajustées à angle droit, utilisée soit pour vérifier des angles dièdres droits, soit pour tracer des angles plans droits. Source : http://fr.wikipedia.org/wiki/%C3%89querre
Dessins et plans, Géométrie, Cercles, Automobiles -- Essuie-glace, Essuie-glace, Automobiles -- Pare-brise, Technologie
Essuie-glace antagoniste
Essuie-glace à disposition centrée-symétrique ou antagoniste : essuyage opposé.
Dessins et plans, Géométrie, Cercles, Automobiles -- Essuie-glace, Essuie-glace, Automobiles -- Pare-brise, Technologie
Essuie-glace inversé
Essuie glace antagoniste inversé, placé au repos dans l'habillage de chaque pilier du pare-brise.
Dessins et plans, Géométrie, Triangle, Mathématiciens, Itération (mathématiques), Algorithmes, Savants polonais, Wacław Sierpinski (1882-1969), Fractales, Récursivité, Théorie de la
Évolution du triangle de Sierpinski
Évolution du triangle de Wacław Sierpinski (1882-1969) en 5 itérations. Un algorithme pour obtenir des approximations arbitrairement proches du triangle de Sierpiński peut s'écrire de la manière suivante : 1-Commencer à partir d'un triangle quelconque du plan. Le triangle canonique de Sierpiński se construit à partir d'un triangle équilatéral ayant une base parallèle à l'axe des abscisses ; 2-Tracer les trois segments qui joignent deux à deux les milieux des côtés du triangle, ce qui délimite 4 nouveaux triangles ; 3-Enlever le petit triangle central. Il y a maintenant trois petits triangles qui se touchent deux à deux par un sommet, dont les longueurs des côtés sont la moitié de celles du triangle de départ (obtenue par une homothétie de rapport 1/2), et dont l'aire est divisée par 4. 4-Recommencer à la deuxième étape avec chacun des petits triangles obtenus.
Photographie, Géométrie, Peinture et décoration murales, Façades, Mosaïques, Illusions d'optique, Art contemporain, Art optique, Art abstrait, Op art, Victor Vasarely (1908-1997)
Façade de théâtre par Vasarely
Façade du théâtre de Győr en Hongrie, mosaïque de Victor Vasarely (1908-1997).
Gravure, Géométrie, Art médiéval -- Europe, Manuscrits à enluminures, Allégories -- Dans l'art, Allégories (mathématiques)
Femme enseignant la géométrie au Moyen Âge
Détail d'une enluminure du XIVe siècle, contrepoinçon d'une lettre capitale P, au début des Éléments d'Euclide, dans une traduction attribuée à Adélar de Bath. Une femme porte une équerre d'une main et utilise un compas de l'autre pour mesurer des distances sur un diagramme. Un groupe de moines, apparemment ses étudiants, la regardent. Au Moyen Âge, la représentation d'une femme dans un rôle d'enseignant est inhabituelle. La femme représentée ici serait donc plutôt une personnification de la géométrie.
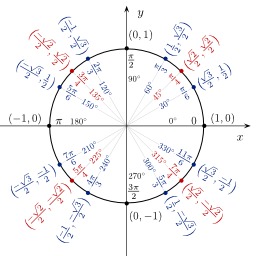
Fonctions trigonométriques dans le cercle unité
Représentation des fonctions trigonométriques dans le cercle unité. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre 0 et π/2. Sur ce cercle sont représentés certains angles communs, et sont indiquées leurs mesures en radians figurant dans l'intervalle [–2π, 2π], soit deux mesures par angle et même trois pour l'angle nul. Notez que les angles positifs sont dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive Ox de l'axe des abscisses coupe le cercle en un point de coordonnées (cos θ, sin θ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
Photographie, Géométrie, Antiquités gallo-romaines, Bordeaux (Gironde), Mosaïques, Burdigala (ville ancienne), Bordeaux (Gironde) -- Musée d'Aquitaine, sylvanus-aquitaine
Fragment de mosaïque géométrique de Burdigala
Fragment de mosaïque de Burdigala, Musée d'Aquitaine à Bordeaux. Découverte de 1876, 41 rue du Pas-Saint-Georges (angle de la rue Bergère) : tesselles en marbre et en terre cuite.
Photographie, Géométrie, Montréal (Canada), Stations de métro, Art contemporain, Décorations murales
Fresque dans le métro de Montréal
Cadillac, métro de Montréal : Murales dans les couloirs d'accès à base de formes ovales et de couleurs chaudes et froides. Jean Cartier, 1976, acier émaillé.
Geometria (Geometry).jpg
Scan by Nick Michael d'une gravure de Beham, (Hans) Sebald (1500-1550): Geometria (B.126, P.128), from The Seven Liberal Arts, P., Holl. 123-129.
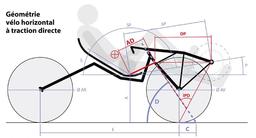
Géométrie du vélo horizontal à traction directe
Géométrie du vélo horizontal à traction directe : Un vélo couché à traction directe se différencie du vélo couché traditionnel par son pédalier, solidaire de la direction. La plupart des vélos couché sont dits "à propulsion". Leur géométrie est calquée sur celles des vélos droits, ou bicyclettes. La chaîne transmet la force du pédalier à la roue arrière, passant par toute la longueur du cadre. Si celui-ci n'est pas extrêmement rigide, une bonne partie de l'énergie fournie au pédalier est perdue. La géométrie du vélo à traction directe permet de minimiser cette perte en transmettant l'énergie à la roue avant. La conséquence est que le pédalier tourne avec la direction, nécessitant un apprentissage. L'appui sur les pédales influence la direction. On parle d'interaction pédalage/direction. Ce modèle fourni les paramètres recommandés afin d'obtenir un vélo qui soit le plus stable possible et dont l'interaction pédalage/direction soit des plus faibles. Les pourcentages indiquent l'importance de certains paramètres par rapport aux autres afin d'assurer une stabilité maximale. Plus le pourcentage est bas, moins une variation du paramètre a d'influence sur la conductabilité du vélo. La maîtrise du pilote est l'élément primordial. Une grande interaction pédalage-direction devient inexistante après plusieurs centaines de km. Respecter ces paramètres aide à avoir un vélo le plus stable possible. L'apprentissage fait le reste. En basse vitesse, c'est l'utilisateur/trice qui crée l'équilibre. A haute vitesse, les forces auto-stabilisantes sont prépondérantes. Un appui naturel de la jambe part du fémur du même côté. Pour que la force passe par l'axe D et ainsi annuler l'interaction PD, il faut inverser cet appui. Lorsque la jambe droite appuie, c'est la hanche côté gauche qui reçoit l'appui.
Gravure, Géométrie, Versailles (Yvelines) -- Château, Surfaces (mathématiques) -- Volumes, Allain Manesson-Mallet (1630-1706)
Géométrie pratique en 1702
Formes géométriques surmontées d'une vue de la Petite Écurie, où Manesson Mallet enseignait les mathématiques. "Des cylindres, hémisphères, colonnes, segmens, ou portions de sphères, cônes, etc." par Allain Manesson-Mallet, La Géométrie pratique, t. I, Paris, Anisson, 1702. (Géométrie pratique, t. 1, planche XXXIX).
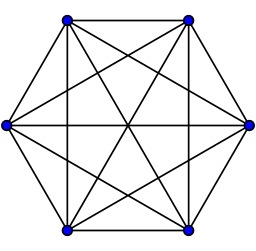
Graphe à six côtés
En théorie des graphes, le graphe complet K_n est l'unique graphe à isomorphisme près possédant n sommets tous reliés deux à deux par une arête, ici 6.
Dessins et plans, Géométrie, Solides, Tétraèdres, Polyèdres, Groupes de rotations, Symétrie, Symétrie (physique)
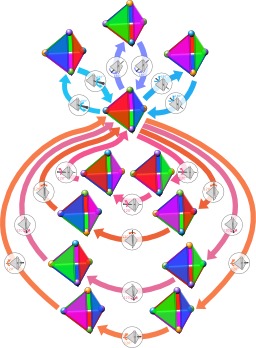
Groupe de symétrie du tétraèdre régulier
Un tétraèdre régulier peut être placé dans 12 positions distinctes par une seule rotation. Celles-ci sont illustrées dans le format d'un graphe de cycles avec des rotations à 180° par rapport à une arête (flèches bleues) et à 120° par rapport à un sommet (flèches rouges) qui permutent le tétraèdre dans toutes les positions. Les 12 rotations forment le groupe (de symétrie) de rotation de la figure.
Guillochis sur couvercle émaillé
Exemple de guillochis sur un couvercle émaillé. Le guillochis est notamment utilisé comme élément décoratif en architecture, en joaillerie, en coutellerie et en ébénisterie. Présent sur les billets de banque et les documents d'identité, c'est aussi un élément de sécurité visant à compliquer la tâche des faussaires.
Dessins et plans, Géométrie, Carré, Personnages de bandes dessinées, dessins animés, etc., Sourire, Humour, Formes (mathématiques)
Hervé le carré
Hervé le carré, héros de "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Formes (mathématiques), Odysseus, Collines, Personnages imaginaires
Hervé le carré au sommet de la colline
Hervé le carré au sommet de la colline, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Humour, Formes (mathématiques), Odysseus, Personnages imaginaires
Hervé le carré décide de s'arrondir
Hervé le carré décide de s'arrondir, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Formes (mathématiques), Odysseus, Collines, Personnages imaginaires
Hervé le carré et la colline du Trapèze
Hervé le carré et la colline du Trapèze, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Coeur, Humour, Relations amoureuses, Formes (mathématiques), Odysseus, Personnages imaginaires, Cour amoureuse, Déclarations d'amour
Hervé le carré rêve
Hervé le carré rêve, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
Dessins et plans, Géométrie, Carré, Coeur, Humour, Relations amoureuses, Formes (mathématiques), Coeur -- Folklore, Personnages imaginaires
Hervé le carré tombe amoureux de Cléandre la ronde
Hervé le carré tombe amoureux de Cléandre la ronde, in "Le carré qui voulait devenir rond", histoire imaginée par Odysseus pour Noël 2014. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
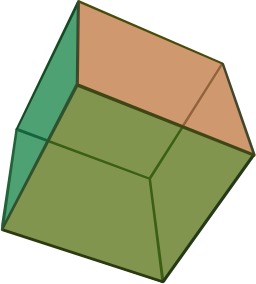
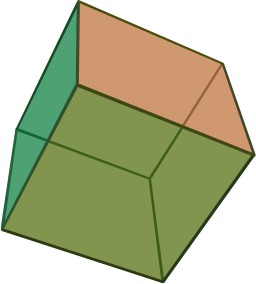
Hexaèdre régulier, le cube
En géométrie des solides, un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube. Le terme hexaèdre vient du grec heksaedros et du bas latin hexahedrum, ce qui justifie la présence de la lettre h dans la traduction anglaise "hexahedron".
Photographie, Géométrie, Illusions d'optique, Art contemporain, Art optique, Caracas (Venezuela), Art abstrait, Op art, Victor Vasarely (1908-1997), Casimir Malevitch (1878-1935)
Hommage à Malévitch de Vasarely
"Hommage à Malévitch", 1954, par Victor Vasarely, Université centrale du Venezuela à Caracas.