Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Compas, Parallèles (géométrie), Constructions géométriques, Milieux (géométrie), Segments (géométrie)
Construction au compas du milieu d'un segment
Construction au compas seul du milieu d'un segment : Le point A' est le symétrique de A par rapport à B. Les cercles de centre A' passant par A et de centre A passant par B se rencontrent en C et D. Le point D' est le symétrique de D par rapport à A. I est le quatrième point du parallélogramme AD'CI.
Dessins et plans, Géométrie, Compas, Règles, Parallèles (géométrie), Symétrie, Constructions géométriques
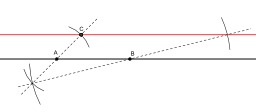
Construction d'une parallèle
Construction à la règle et au compas d'une parallèle à une droite passant par un point donné : La parallèle à la droite (AB) passant par un point C se construit à l'aide de la propriété de la droite des milieux. On construit le symétrique C1 du point C par rapport à A puis le symétrique C2 du point C1 par rapport à B. la droite recherchée est la droite (CC2). Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès.
Photographie, Gravure, Parallèles (géométrie), Dessin industriel, Arts plastiques, Dessin technique, Hachurateurs
Hachurateur
Pour tracer des hachures parallèles équidistantes, on peut s'aider d'un hachurateur (instrument constitué par une règle qui se déplace d'une valeur donnée en appuyant sur un bouton). Le hachurateur consiste en une règle, généralement graduée, qui peut se déplacer dans une seule direction, perpendiculairement. Pour cela, elle est équipée d'un ou deux rouleaux sur lesquels elle peut avancer ou reculer, sans dévier de son axe primitif. Des repères, ou dans les systèmes plus élaborés, un mécanisme permettent de reculer selon la valeur désirée. Le hachurateur, dont l'usage, comme pour la plupart des outils de dessin technique, a été rendu obsolète par le développement de l'informatique, était utilisé dans le dessin technique et artistique, l'héraldique, etc. Dans la technique du trait anglais, sorte d'imitation de le gravure sur carte à gratter, il permet d'obtenir des valeurs de gris régulières.
Photographie, Dessins et plans, Géométrie, Carré, rectangle, rectangles, Angles, Parallèles (géométrie), Parallélogrammes, Polygones, Tablettes d'argile cunéiformes, Pentagones, Diagonales, Racine carrée de deux, Losanges, Quadrilatères, Trapèzes, Aires (surfaces), Aires (surfaces) -- Mesure
Parallélograme
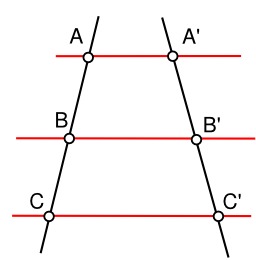
Exemple de parallélogramme. Un parallélogramme, en géométrie, est un quadrilatère dont les côtés opposés sont parallèles deux à deux
Dessins et plans, Géométrie, Parallèles (géométrie), Thalès, Théorème de, Constructions géométriques, Triangles (géométrie)
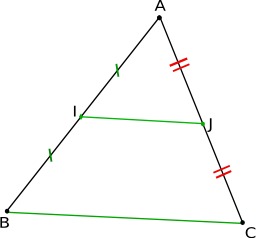
Réciproque du théorème de Thalès
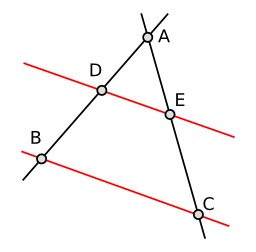
Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès. Si un segment a pour extrémités les milieux de deux côtés d’un triangle, alors il est parallèle au troisième côté, et sa longueur est égale à la moitié de celle de ce troisième côté. Soient I et J les milieux respectifs des segments [AB] et [AC], alors (IJ) // (BC) et IJ = BC ÷ 2.
Dessins et plans, Géométrie, Règles, Dessin -- Matériel, Parallèles (géométrie), Dessin -- Instruments, Dessin -- Technique, Lignes du quadrillage
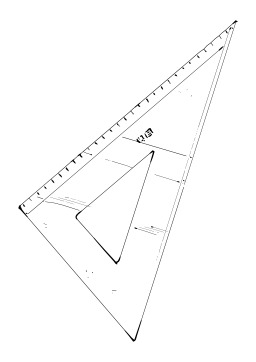
Tracer une parallèle avec une règle et une équerre
Métode pour tracer une parallèle avec une règle et une équerre. On prend une équerre et l'on appuie un côté sur la droite de référence. On place une règle contre un autre côté de l'équerre. Puis, on appuie fermement sur la règle, et l'on fait glisser l'équerre contre la règle sans appuyer sur l'équerre, ceci afin d'éviter de faire bouger la règle. Source : Mécanique pour l'enseignement technique industriel/Éléments de géométrie (fr.wikiversity.org ).