Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Calcul, Calculatrices de poche, Mathématiques, Mathématiques -- Étude et enseignement, Piles solaires
Calculatrice solaire des années 80
Calculatrice] solaire extra-plate ; Affichage par cristaux liquides à huit chiffres ; Source d'alimentation : cellule photovoltaïque incorporée ; Format type « carte de crédit » ; Dimensions : 86 x 54 x 2,5 mm ; Masse : 14,3 g ; Années 1980.
Carré magique
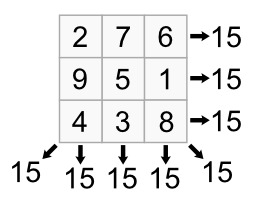
Carré magique normal d’ordre 3 et de constante magique 15. En mathématiques, un carré magique d’ordre n est composé de n^{2} nombres entiers, écrits sous la forme d’un tableau carré. Ces nombres sont disposés de sorte que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales. On nomme alors constante magique (et parfois densité) la valeur de ces sommes.
Dessins et plans, Calcul, Jeux mathématiques, Influence japonaise, Kakuro, Combinaisons (mathématiques), Jeux logiques
Combinaisons de nombres pour le jeu japonais du kakuro - 1
Combinaisons de nombres pour le jeu japonais du kakuro : possibilités de décompositions de sommes de nombres différents de 3 à 24.
Combinaisons de nombres pour le jeu japonais du kakuro - 2
Combinaisons de nombres pour le jeu japonais du kakuro : possibilités de décompositions de sommes de nombres différents de 25 à 45.
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
Construction d'un carré magique par la méthode du losange - 1
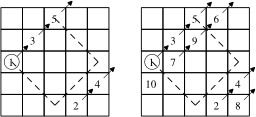
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
Construction d'un carré magique par la méthode du losange - 2
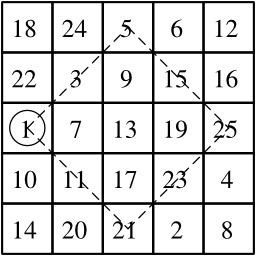
Un carré magique 5x5 construit selon la méthode du losange proposée par John Horton Conway : Le résultat final est un carré magique dont la constante est 65.
Construction de carrés magiques, nombres pairs
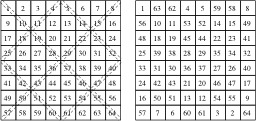
Construction d'un carré magique 8x8 selon la méthode des permutations relativement aux diagonales des sous-damiers 4x4. Dans le carré de gauche, les nombres naturels sont inscrits dans l'ordre. De plus, les diagonales principales de chaque sous-damier 4x4 sont recouvertes de lignes en pointillés. À droite, le carré final, magique, est inscrit. Chaque nombre qui n'était pas recouvert par une ligne en pointillés a été remplacé par son complément à (82 + 1) = 65.
Dessins et plans, Calcul, Horloges et montres, Arithmétique, Aiguilles (horlogerie), Arithmétique modulaire
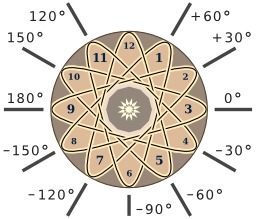
Correspondances heures et angles
Douze angles définis modulo 360 degrés correspondent à des temps, définis modulo 12 heures. Par exemple, une aiguille d’horloge a une seule position numérotée zéro ou vingt-quatre, parce que 0 = 24 modulo 12. Cette position correspond à 90 ou –270 degrés modulo 360 degrés. Ainsi nous identifions direction et sens d’une demi-droite ou d’un vecteur en coordonnées polaires, ou l’angle d’une rotation donnée, ou l’argument d’un nombre complexe donné. Le dessin sur le cadran de l’horloge évoque des progressions arithmétiques de raisons 5 ou 7 modulo 12. Par exemple, en tournant dans le sens des aiguilles d’une montre à partir de 1, nous passons par les termes : 1, 6, 11, 4, 9, 2, 7, 12, 5, 10, 3, 8. Cette suite correspond à une progression de raison arithmétique 210 degrés modulo 360 degrés. Si les douze positions d’une aiguille d’horloge sont numérotées dans l’ensemble P de douze éléments, de 1 à 12 modulo 12, et si l’ensemble A est constitué des angles indiqués dans l’image, une bijection B de P sur A peut être définie par B( t ) = 90 – 30 t. Par exemple, B( 12 ) = 90 – 30 × 12 = 90 degrés modulo 360 degrés. L'arithmétique modulaire est un système arithmétique d'entiers modifiés, où les nombres sont « abaissés » lorsqu'ils atteignent une certaine valeur. Donnons comme exemple, l'« arithmétique de l'horloge » qui se réfère à l'« addition » des heures indiquées par la petite aiguille d'une horloge : concrètement, si nous commençons à 9 heures et ajoutons 4 heures, alors plutôt que de terminer à 13 heures (comme dans l'addition normale), nous sommes à 1 heure. De la même manière, si nous commençons à minuit et nous attendons 7 heures trois fois de suite, nous nous retrouvons à 9 heures (au lieu de 21). Fondamentalement, quand nous atteignons 12, nous recommençons à zéro ; nous travaillons modulo 12. Pour reprendre l'exemple précédent, on dit que 9 et 21 sont congrus modulo 12. Les nombres 9 ; 21 ; 33 ; 45 ; etc. sont considérés comme égaux lorsqu'on travaille modulo 12. Pour généraliser, nous pouvons facilement imaginer une horloge qui contient un nombre arbitraire d'heures, et faire des calculs avec un nouveau modulo.
Photographie, Calcul, Ustensiles de cuisine, Cuisine, Moules à pâtisserie, Canelés, Cuisine bordelaise, Rangées
Deux moules à canelés bordelais
Deux moules souples an silicone pour 18 mini-cannelés bordelais : 3 rangées de 6 ou 6 rangées de 3...
Photographie, Calcul, Carré, Jeux mathématiques, Dominos (jeu), Matériel didactique, Vulgarisation scientifique, Écrivains russes pour la jeunesse, Matériel pédagogique, Intellectuels russes, Yakov Perelman (1882-1942)
Jeu mathématique avec des dominos
Un des carrés possibles du jeu de Yakov Perelman (1882-1942), professeur russe : quatre dominos formant un carré sont disposés de façon à ce que le nombre de points de chacun des cotés soit identique.
Margarita Philosophica - Arithmetica, 1508
Fragment d'une gravure sur bois (Grégoire Reisch, 1508) : l'Arithmétique présente un concours entre Boèce (Boetius) et Pythagoras (Pythagore). Ce dernier, manipulant un abaque antique (genre de boulier) peu pratique, est présenté fort embarrassé face à Boèce réjoui qui, ayant usé du calcul décimal et des chiffres indo-arabes, semble avoir terminé.
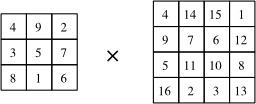
Multiplication de deux carrés magiques - 1
Multiplication de deux carrés magiques : Soit à effectuer le « produit » de ces deux carrés magiques, un de 3x3 et l'autre de 4x4. Le carré magique final sera de 12x12. Le « produit » de deux carrés magiques crée un carré magique d'ordre supérieur aux deux multiplicandes. Ce produit s'effectue ainsi. Soit les carrés magiques M et N : 1) Le carré final sera d'ordre MxN ; 2) Diviser le damier final en NxN sous-damiers de MxM cases ; 3) Dans le carré N, réduire de 1 la valeur de tous les nombres ; 4) Multiplier ces valeurs réduites par M × M. Les résultats sont reportés dans les cases de chaque sous-damier correspondant du carré final ; 5) Les cases du carré M sont additionnées NxN fois aux cases du damier final. Source : http://fr.wikipedia.org/wiki/Carr%C3%A9_magique_%28math%C3%A9matiques%29.
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
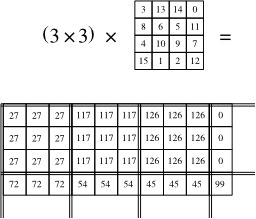
Multiplication de deux carrés magiques - 2
Deuxième étape de la multiplication des deux carrés magiques (3 et 4) : Le carré magique de 3x3 est remplacé par le produit (3 × 3), alors que chaque nombre du carré 4x4 est diminué de 1. Le damier final, de taille 12x12, est divisé en 4x4 sous-damiers, chacun ayant 3x3 cases. Chacune de ses cases s'obtient en multipliant (3 × 3) par l'une des cases du carré magique 4x4 « diminué ». Par exemple, 117 est le produit de 3 × 3 × 13. Ce carré est magique, mais n'est pas normal. La prochaine étape va « corriger » cette « anomalie ».
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
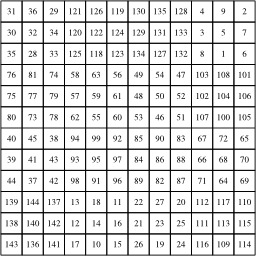
Multiplication de deux carrés magiques - 3
Multiplication de deux carrés magiques, dernière étape : Après 4x4 additions du carré 3x3, le carré final est magique et normal.
Quatre lapins de 1 à 4
Quatre lapins de 1 à 4, logiciel libre Calculs d'Abulédu, par E. François et F. Audirac, 20090823.
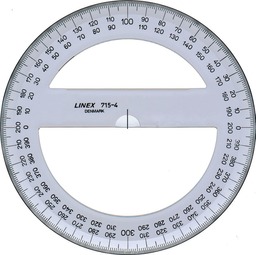
Rapporteur
Un rapporteur (ou rapporteur d'angle) est un outil utilisé en géométrie pour mesurer des angles et pour construire des figures géométriques.