Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Nombres, Chiffres, Idiosyncrasie, Imagerie (psychologie), Images mentales, Jeux arithmétiques
Arithmétique idiosyncratique
1892-1893. Source : Popular Science Monthly, Volume 42, "Number forms", par G. T. W. Patrick, professeur de philosophie à l'université d'Iowa. Illustration d'une remarque Miss H. R. Hudson (Atlantic Monthly for February, 1873) sur les idiosyncrasies : Les neuf chiffres montent directement à la verticale, et les suivants suivent en diagonale.
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Coeur, Nombres, Chiffres, As (cartes à jouer)
As de coeur
Schéma d'un as de cœur. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "1".
Combinaisons de nombres pour le jeu japonais du kakuro - 2
Combinaisons de nombres pour le jeu japonais du kakuro : possibilités de décompositions de sommes de nombres différents de 25 à 45.
Hexagone magique (3)
Hexagone magique d'ordre 3 : les nombres de 1 à 19 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 38. En mathématiques, un hexagone magique d'ordre n est un arrangement de nombres formant un gabarit hexagonal centré avec n cellules sur chaque côté. La somme des nombres dans chaque rangée ou dans les trois directions font la même somme. Un hexagone magique normal contient tous les entiers allant de 1 à 3n2 − 3n + 1. Il existe seulement deux arrangements respectant ces conditions, celui d'ordre 1 et celui d'ordre 3. De plus, la solution d'ordre 3 est unique.
Hexagone magique (4)
Hexagone magique (4 cases par côté) : les nombres de 3 à 38 sont placés dans cette grille hexagonale pour que la somme des nombres de chaque rangée soit égale à 111.
Hexagone magique (5)
Hexagone magique d'ordre 5 : les nombres de 6 à 66 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 244.
Hexagone magique (7)
Hexagone magique d'ordre 7 : les nombres de 2 à 128 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 635.
Photographie, Nombres, Raisin, Vignes, Saint-Pétersbourg (Russie), Saint-Petersbourg (Russie) -- Cathédrale Saint-Pierre-et-Saint-Paul
L'arbre des nombres à Saint-Pétersbourg
L'arbre des nombres à Saint-Pétersbourg : vigne du Prince Vladimir à la Cathédrale de Saint-Pétersbourg, Russie.
Dessins et plans, Nombres, Chiffres, Humour, Logiciels libres, Lapins, Opérations mathématiques, Calculs numériques, AbulÉdu
Le lapin calculateur du terrier d'Abulédu
Le lapin calculateur du terrier d'Abulédu, par E. François et F. Audirac, 20080101.
Dessins et plans, Écriture -- Matériel et instruments, Acrobatie, Nombres, Numération, Coloriages, Dessin en noir et blanc, Skateboard (sports), Skateboarders, Skateurs
Les nombres du skateur
Les nombres du skateur, de 10 à 19 et les dizaines jusqu'à 100, à colorier.
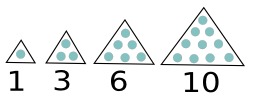
Nombres triangulaires
Représentation graphique des premiers nombres triangulaires : la représentation figurée permet un calcul pour les premières valeurs. Une définition formelle s'obtient par récurrence : le nombre triangulaire d'indice 1 est égal à 1, et un nombre triangulaire est égal à son prédécesseur additionné de son indice. Les premiers nombres triangulaires sont : 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ... Il existe différentes manières de calculer le nombre triangulaire d'indice n, l'une d'elles est graphique et s'obtient par un raisonnement d'arithmétique géométrique.
Dessins et plans, Nombres cardinaux, Matériel didactique, Nombres, Chiffres, Addition, Numération, Outils pédagogiques, Tables mathématiques, Tables numériques
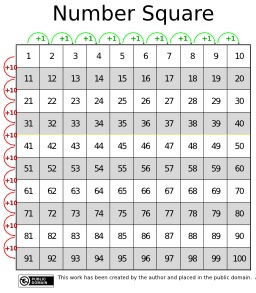
Table d'addition jusqu'à 100
Table d'addition jusqu'à 100 : +1 à l'horizontale, +10 à la verticale.
Photographie, Douze (le nombre), Blanc, Nombres, Chiffres, Numérotage (télécommunications), Alphabet, Lettres de l'alphabet, Téléphone -- Appareils et matériel, Communication téléphonique, Téléphones, Lettres capitales, Claviers (électronique), Années 60 (vingtième siècle), Commande numérique
Téléphone des années 60
Téléphone des années 60 avec vingt-quatre lettres et dix chiffres sur les douze touches du clavier : 1 ; 2, ABC ; 3, DEF ; 4, GHI ; 5, JKL ; 6, MNO ; 7, PRS ; 8, TUV ; 9, WXY ; * ; 0, Oper ; #
Dessins et plans, Géométrie, Aires (surfaces), Aires (surfaces) -- Mesure, Nombres transcendants, Pi (le nombre), British library -- Manuscrits. Papyrus 10188, Papyrus Bremner-Rhind
Approximation de PI par Ahmès
Illustration de l'approximation de π (PI) par Ahmès (Égypte). Découvert en 1855, le papyrus de Rhind contient le texte, recopié vers l’an 1650 avant notre ère par le scribe égyptien Ahmès, d’un manuel de problèmes pédagogiques très ancien. On y trouve une méthode pour évaluer l’aire d’un disque en prenant le carré dont le côté est égal au diamètre du disque diminué d’un neuvième. Cette méthode conduit à une évaluation de π de 256/81. Dans l’illustration ci-contre, le disque a pour diamètre 9. L’aire du disque est légèrement supérieure à l’aire de l’octogone irrégulier obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l’aire du disque est alors évaluée à 64 soit l’aire d’un carré de côté 8. Le rapport entre l’aire du disque et le carré du rayon est alors évalué par 64/(9/2)^2, c’est-à-dire 256/81.
Dessins et plans, Abaques (mathématiques), Arithmétique, Unités arithmétiques et logiques, Cinq (le nombre), Multiplication (arithmétique), Bouliers
Boulier-Abaque
Croquis d'un abaque boulier : les unités sont placées en haut de la tige inférieure et les multiples de cinq en bas de la tige supérieure ; le nombre se lit donc au milieu du boulier ; chaque colonne peut représenter les nombres de 0 à 15 pour le report des retenues par multiples de 5. Voici le décompte de 1352964708, de gauche à droite : 1 = 1 + 0x5 ; 3 = 3 + 0x5 ; 5 = 0 + 1x5 ; 2 = 2 + 0x5 ; 9 = 4 + 1x5 ; 6 = 1 + 1x5 ; 4 = 4 + 0x5 ; 7 = 2 + 1x5 ; 0 = 0 + 0x5 ; 8 = 3 + 5x1.
Cadran d'horloge aux 48 ponts
On peut considérer que les nombres entiers de 1 à 12, inscrits sur le cadran de l’horloge, sont les douze nombres des heures, ou les numéros de douze virages le long d’une piste de course. Le long de la boucle, il y a quarante-huit ponts. Chaque ligne droite croise huit autres parties de la piste, en passant alternativement en dessous et au-dessus. Avec ce dessin de nœud, il est facile d’expliquer l’arithmétique modulo 12. Par exemple, si maintenant il est onze heures, dans cinq heures l’aiguille de l’horloge indiquera quatre heures, parce que 11 + 5 = 4 modulo 12. En tournant dans le sens des aiguilles d’une montre, on passe par les termes d’une progression arithmétique de raison +5 ou –7. Cela explique aussi "{12,5}" : une notation de Schläfli qui désigne des dodécagones réguliers étoilés, tous semblables.
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres non-rationnels, Nombres transcendants, Pi (le nombre)
Calcul de l'aire du cercle avec Géogébra
Calcul de l'aire du cercle avec Géogébra : rayon x demi-circonférence. On déduit d’une propriété analogue pour les polygones réguliers que l’aire d’un cercle égale son demi-périmètre multiplié par son rayon. le périmètre du polygone est à peu près 2πr alors qu’en redistribuant les triangles formés on remarque que son aire est à peu près πr2. Pour formaliser le « à peu près » il faudrait faire tendre le nombre de côtés du polygone vers l’infini, ce qui illustre déjà la nature « analytique » de π.
Dessins et plans, Cube, Carré, Géométrie des nombres, Gnomonique, Abu Bakr Muhammad ibn al-Hasan al- Karaji (....-1019 ?)
Carré d'un nombre triangulaire
Démonstration géométrique de la formule donnant le carré d'un nombre triangulaire, égal à la somme des premiers cubes parfaits : le carré du nième nombre triangulaire est égal à la somme des n premiers cubes. L'illustration géométrique permet de se convaincre de la véracité de ses propositions. L'aire de la zone orange de la figure est appelée nombre gnomonique. Elle est constituée de deux rectangles de base 4 et de côté le nombre triangulaire d'indice 4, c'est-à-dire 10. Ces deux rectangles se recoupent sur un carré de côté 4, on en déduit que l'aire orange est égale à 5 x 4 x 4 - 4 x 4, ou encore 43. Ce raisonnement est valable sur chaque nombre gnomonique, l'aire du carré de côté le nombre triangulaire d'indice 4 est égal la somme des 4 premiers cubes. De cette démonstration d'Al-Karaji, on déduit la première proposition.
Carré magique
Carré magique normal d’ordre 3 et de constante magique 15. En mathématiques, un carré magique d’ordre n est composé de n^{2} nombres entiers, écrits sous la forme d’un tableau carré. Ces nombres sont disposés de sorte que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales. On nomme alors constante magique (et parfois densité) la valeur de ces sommes.
Chemins binaires dans le triangle de Pascal
Les quatre chemins binaires dans le triangle de Pascal : Imaginons que chaque nombre dans le triangle est un nœud dans un réseau qui est connecté aux nombres adjacents du dessus et du dessous. Maintenant pour n'importe quel nœud dans le réseau, comptons le nombre de chemins qu'il y a dans le réseau (sans faire marche arrière) qui connecte ce nœud au nœud supérieur du triangle. La réponse est le nombre de Pascal associé à ce nœud.
Dessins et plans, Musique, Mesures, Musique -- Lecture et déchiffrage, Partitions (musique), Solfège, Notes (musique), Partitions -- Lecture et déchiffrage, Mesure, Mesures (musique)
Chiffrage des mesures en solfège
Les deux nombres du chiffrage forment une fraction (sans la barre horizontale) dont l'unité de valeur est toujours la ronde. Le chiffrage 4/4 est parfois représenté par un "C", et le chiffrage 2/2 par un "C barré". Source : http://fr.wikipedia.org/wiki/Mesure_%28solfege%29
Dessins et plans, Calcul, Jeux mathématiques, Influence japonaise, Kakuro, Combinaisons (mathématiques), Jeux logiques
Combinaisons de nombres pour le jeu japonais du kakuro - 1
Combinaisons de nombres pour le jeu japonais du kakuro : possibilités de décompositions de sommes de nombres différents de 3 à 24.
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
Construction d'un carré magique par la méthode du losange - 1
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
Construction de carrés magiques, nombres pairs
Construction d'un carré magique 8x8 selon la méthode des permutations relativement aux diagonales des sous-damiers 4x4. Dans le carré de gauche, les nombres naturels sont inscrits dans l'ordre. De plus, les diagonales principales de chaque sous-damier 4x4 sont recouvertes de lignes en pointillés. À droite, le carré final, magique, est inscrit. Chaque nombre qui n'était pas recouvert par une ligne en pointillés a été remplacé par son complément à (82 + 1) = 65.
Dessins et plans, Calcul, Horloges et montres, Arithmétique, Aiguilles (horlogerie), Arithmétique modulaire
Correspondances heures et angles
Douze angles définis modulo 360 degrés correspondent à des temps, définis modulo 12 heures. Par exemple, une aiguille d’horloge a une seule position numérotée zéro ou vingt-quatre, parce que 0 = 24 modulo 12. Cette position correspond à 90 ou –270 degrés modulo 360 degrés. Ainsi nous identifions direction et sens d’une demi-droite ou d’un vecteur en coordonnées polaires, ou l’angle d’une rotation donnée, ou l’argument d’un nombre complexe donné. Le dessin sur le cadran de l’horloge évoque des progressions arithmétiques de raisons 5 ou 7 modulo 12. Par exemple, en tournant dans le sens des aiguilles d’une montre à partir de 1, nous passons par les termes : 1, 6, 11, 4, 9, 2, 7, 12, 5, 10, 3, 8. Cette suite correspond à une progression de raison arithmétique 210 degrés modulo 360 degrés. Si les douze positions d’une aiguille d’horloge sont numérotées dans l’ensemble P de douze éléments, de 1 à 12 modulo 12, et si l’ensemble A est constitué des angles indiqués dans l’image, une bijection B de P sur A peut être définie par B( t ) = 90 – 30 t. Par exemple, B( 12 ) = 90 – 30 × 12 = 90 degrés modulo 360 degrés. L'arithmétique modulaire est un système arithmétique d'entiers modifiés, où les nombres sont « abaissés » lorsqu'ils atteignent une certaine valeur. Donnons comme exemple, l'« arithmétique de l'horloge » qui se réfère à l'« addition » des heures indiquées par la petite aiguille d'une horloge : concrètement, si nous commençons à 9 heures et ajoutons 4 heures, alors plutôt que de terminer à 13 heures (comme dans l'addition normale), nous sommes à 1 heure. De la même manière, si nous commençons à minuit et nous attendons 7 heures trois fois de suite, nous nous retrouvons à 9 heures (au lieu de 21). Fondamentalement, quand nous atteignons 12, nous recommençons à zéro ; nous travaillons modulo 12. Pour reprendre l'exemple précédent, on dit que 9 et 21 sont congrus modulo 12. Les nombres 9 ; 21 ; 33 ; 45 ; etc. sont considérés comme égaux lorsqu'on travaille modulo 12. Pour généraliser, nous pouvons facilement imaginer une horloge qui contient un nombre arbitraire d'heures, et faire des calculs avec un nouveau modulo.
Dessins et plans, Géométrie, Cauchy (Augustin Louis, baron), 1789-1857, Dodécaèdres, Polyèdres, Projection stéréographique
Dodécaèdre
Le dodécaèdre, un polyèdre régulier convexe. En 1811, Cauchy (1789-1857) s’intéresse dans son premier mémoire à l’égalité de polyèdres convexes dont les faces sont égales. Il propose une démonstration du théorème de Descartes-Euler, concernant les nombres de sommets, de faces et d'arêtes d'un polyèdre convexe. Sa preuve consiste à projeter le polyèdre en un graphe planaire suivant ce qui est aujourd’hui appelé une projection stéréographique. Cependant, Cauchy commit une erreur, en ne faisant pas d’hypothèse claire sur les polyèdres étudiés. Dans son second mémoire en 1812, il donna des formules pour calculer les angles diédraux.
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres transcendants, Pi (le nombre)
Encadrement de PI par Liu Hui
Représentation de l'encadrement de π par Liu Hui. Si les calculs pratiques peuvent se faire avec une bonne précision en utilisant la valeur 3,14 comme approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416.
Photographie, Dix-neuvième siècle, Temps -- Mesure, Horloges à automates, Automates, Horloges astronomiques, Horlogers, Besançon (Doubs) -- Cathédrale Saint-Jean
Horloge astronomique de Besançon
L'Horloge astronomique de la cathédrale Saint-Jean de Besançon est une horloge astronomique considérée comme un chef-d'œuvre du genre, construite par Auguste-Lucien Vérité au XIXe siècle, célèbre maître horloger de Beauvais en Picardie (concepteur de l'horloge astronomique de Beauvais de la cathédrale Saint-Pierre de Beauvais entre 1865 et 1868). L'horloge de Vérité est composée de 30 000 pièces mécaniques et présente 122 indications toutes interdépendantes dont : heures, dates, saisons, durée du jour et de la nuit, heures à 20 endroits du monde, nombres d'éclipses lunaires et solaires, signes zodiacaux, date de Pâques (épacte), dates et heures des marées, heure solaire, solstice... Cette horloge astronomique est animée par de nombreux automates et chorégraphies mécaniques et animations du système solaire déclenchées en fonction du calendrier et de l'horaire. L'horloge est dans une pièce prévue à cet effet, dans la tour de la cathédrale. Elle peut être visitée tous les jours, en visite guidée exclusivement, aux heures où les animations mécaniques sont les plus spectaculaires. Source : http://fr.wikipedia.org/wiki/Horloge_astronomique_de_Besan%C3%A7on
Photographie, Gares, Horloges et montres, Aiguilles (horlogerie), Rouge, Chiffres romains, Chiffres, Sabres (Landes), Sabres (Landes) -- Airial de Marquèze
Horloge de gare
Photographie de l'horloge de la gare de Sabres avec chiffres romains pour les heures de 1 à 12 et nombres de 13 à 24 ; cadre rouge.
Clip art, Signalisation routière, Panneaux à message variable, Traitement d'images -- Techniques numériques, Traitement vectoriel
Image vectorielle d'Hopital
L'informatique utilise le terme de vecteur, à la fois pour des raisons géométriques et algébriques. Le codage d'une image sur un écran d'ordinateur utilise au choix deux techniques : matricielle et vectorielle. La première utilise des éléments graphiques définis point par point. À chaque pixel est associé la quantité de couleurs primaires correspondante. Si cette méthode est économique en termes de puissance de calcul, un agrandissement de la taille de l'image possède pour conséquence un effet d'escalier. Un dessin vectoriel est une représentation composée d'objets géométriques (lignes, points, polygones, courbes…) ayant des attributs de forme, de position, de couleur, etc. À la différence de la technique précédente, il s'agit d'une méthode plus coûteuse en termes de puissance de calcul mais dans laquelle l'effet d'escalier n'existe pas. La représentation des données en informatique, pour les fonctions de mémoire ou de calcul, se fonde sur des tableaux d'octets. Si un octet est identifié à un scalaire, ce qui se conçoit car deux octets s'additionnent et se multiplient, alors un tel tableau s'apparente à une famille de composantes vectorielles. Pour cette raison, un tel tableau est appelé vecteur. Par extension, le terme de vecteur désigne aussi des tableaux dont les composantes sont autre chose que des nombres, par exemple des pointeurs ou des structures informatiques quelconques.
Peinture, Contes de fées, Petits déjeuners, Fillettes, Or, Bols (vaiselle), Boucles, Personnes blondes, Trois (nombres)
Le conte des trois ours en 1900, p. 13
Le conte des trois ours, 1900, par Leslie Brooke (1862-1940), page 13. Boucle d'or goûta d'abord le grand bol. Source : http://en.wikisource.org/wiki/The_Story_of_the_Three_Bears_%28Brooke%29