Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Anglais (langue), Grilles, Horlogerie, Londres (GB), Architecture, Londres (GB) -- Westminster Palace, Surnoms, Tours -- Angleterre, Charles Barry (1795-1860)
Big Ben à Londres
Big Ben à Londres, Angleterre. Big Ben est le surnom de la grande cloche de 13,5 tonnes installée dans la tour horloge appelée Tour Elizabeth, ou anciennement Clock Tower, du Palais de Westminster, qui est le siège du parlement britannique (Houses of Parliament), à Londres. Style néogothique, architecte Charles Barry, date de construction 1843-1859, hauteur 96,0 m. Source : https://fr.wikipedia.org/wiki/Big_Ben
Casque antique
Ornement en fonte en forme de casque antique, en amortissement d'un pilastre d'une grille de l'École Militaire à Paris.
Photographie, Casques, Grilles, Arts décoratifs, Deux (le nombre), Paris (France) -- École militaire
Deux casques antiques décoratifs
Deux casques antiques décoratifs sur les grilles de l'École militaire à Paris.
Photographie, Clôtures, Cyclomoteurs, Facteurs (postes), Courrier, Grilles, Boîtes aux lettres, Métiers, Melbourne (Australie), Mobylettes, Courrier -- Acheminement
Facteur à moto en Australie
Facteur à moto en Australie distribuant le courrier dans les boîtes aux lettres
Photographie, Métros, Métros -- Stations, Grilles, Ventilation, Montréal (Canada), Art contemporain, Aération
Grille d'aération stylisée à Montréal
Grille d'aération stylisée, métro de Montréal, Marcel Raby : L'œuvre est une intégration à l'architecture et camoufle une bouche de ventilation. Elle est composée de plaques verticales et de tubes aux couleurs olympiques.
Photographie, Grilles, Arts décoratifs, Ferronnerie d'art, Objets en fer forgé, Basse-Autriche (Autriche)
Grille de fenêtre en fer forgé
Grille de fenêtre extérieure en fer forgé, Château des chevaliers teutoniques de l'église de Gumpold en Basse-Autriche.
Photographie, soleil, Grilles, Château de Versailles (Versailles, Yvelines), Couronnes, Portails, Guirlandes, Décoration et ornement architecturaux
Grille dorée du château de Versailles
Partie supérieure du portail de la grille dorée du château de Versailles.
Photographie, soleil, Couronnes (ornement), Grilles, Versailles (Yvelines) -- Château, Fleur de lys, Cornes d'abondance, Architecture, Couronnes, Guirlandes, Décoration et ornement architecturaux
Grille du château de Versailles
Détail d'une des grilles dorées du château de Versailles : soleil, cornes d'abondance, couronne, fleurs de lys et guirlandes.
Photographie, Grilles, Art nouveau (décoration), Coqs, Arts décoratifs, Animaux -- Dans l'art, République, Monogrammes, Paris (France) -- Palais de l'Élysée
Grille du Coq au Palais de l'Élysée
Détail de la "Grille du Coq", à l'arrière du Palais de l'Elysée (palais présidentiel) à Paris. Monogramme RF pour la République Française, de style Art nouveau par l'architecte Adrien Chancel.
Hexagone magique (3)
Hexagone magique d'ordre 3 : les nombres de 1 à 19 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 38. En mathématiques, un hexagone magique d'ordre n est un arrangement de nombres formant un gabarit hexagonal centré avec n cellules sur chaque côté. La somme des nombres dans chaque rangée ou dans les trois directions font la même somme. Un hexagone magique normal contient tous les entiers allant de 1 à 3n2 − 3n + 1. Il existe seulement deux arrangements respectant ces conditions, celui d'ordre 1 et celui d'ordre 3. De plus, la solution d'ordre 3 est unique.
Hexagone magique (4)
Hexagone magique (4 cases par côté) : les nombres de 3 à 38 sont placés dans cette grille hexagonale pour que la somme des nombres de chaque rangée soit égale à 111.
Hexagone magique (5)
Hexagone magique d'ordre 5 : les nombres de 6 à 66 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 244.
Hexagone magique (7)
Hexagone magique d'ordre 7 : les nombres de 2 à 128 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 635.
Photographie, Écureuils, Grilles, Ferronnerie d'art, Objets en fer forgé, Parcs -- Allemagne, Bautzen (Allemagne. - région)
L'écureuil à la grille
Grille d'entrée du Musée d'histoire locale Heimat ‘Carl Swoboda’, à Schirgiswalde en Allemagne.
Photographie, Lanternes, Grilles, Jardins publics, Paris (France) -- Quartier du Jardin des Plantes, Architecture
Lanterne à l'entrée du Jardin des Plantes
Lanterne sur la grille de l'entrée principale du Jardin des Plantes à Paris, (côté Seine, place Valhubert).
Photographie, Grilles, Lapins, Sculpteurs, West Midlands (GB), Réserves naturelles -- Grande-Bretagne
Le lapin gardien
Le lapin gardien de la grille de la réserve naturelle de Holly Wood, dans le comté de Sandwell, en Angleterre, par l'artiste Tim Tolkien, sculpteur anglais contemporain.
Photographie, Grilles, Animaux sauvages, Birmingham (GB), Art contemporain, West Midlands (GB), Réserves naturelles -- Grande-Bretagne, Animaux protégés, Femmes sculpteurs
Les animaux de la réserve
Les animaux de la réserve, grille réalisée par Tim Tolkien pour la réserve naturelle de Sot's Hole, près de Birmingham en Angleterre.
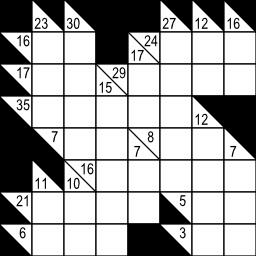
Dessins et plans, Jeux mathématiques, Jeux de logique, Grilles, Influence japonaise, Kakuro, Mots-croisés
Mots-croisés japonais
Grille de Kakuro avec solution, jeu de mots-croisés japonais. Outre la ligne du haut et la colonne de gauche, entièrement noires, la grille, telle une grille de mots-croisés, est divisée en « mots » horizontaux ou verticaux par les cases noires. Les cases noires elles-mêmes sont divisées en deux par une diagonale allant du coin en haut à gauche au coin en bas à droite, de sorte que le "mot" à sa droite et le "mot" au-dessous puissent être définis dans la même case. L'objectif du jeu est de remplir les cases vides (blanches) avec des chiffres entre 1 et 9 de sorte que la somme de tous les chiffres d'un nombre soit égale au nombre inscrit dans la case remplie (noire) définissant le nombre, et qu'un nombre ne puisse pas contenir deux fois le même chiffre. Cette dernière règle est celle qui rend possible la création de grilles à solution unique. Source : http://fr.wikipedia.org/wiki/Kakuro.
Photographie, Grilles, Ferronnerie d'art, Jean Lamour (1698-1771), Nancy (Meurthe-et-Moselle) -- Place Stanislas
Nancy, Place Stanislas
Nancy, grilles de la Place Stanislas par Jean Lamour (1698-1771) est un serrurier et ferronnier lorrain au service du roi de Pologne, duc de Lorraine, Stanislas Leszczynski.
Puzzle d'Euler
Problème d'Euler des 36 officiers : un carré gréco-latin d’ordre 6 est impossible à résoudre. En 1782, le mathématicien suisse Leonhard Euler imagine un problème dans une grille. Certains attribuent donc la paternité du sudoku au Suisse, bien que les travaux d’Euler concernent les carrés latins et la théorie des graphes. On considère six régiments différents, chaque régiment possède six officiers de grades distincts. On se demande maintenant comment placer les 36 officiers dans une grille de 6×6, à raison d’un officier par case, de telle manière que chaque ligne et chaque colonne contienne tous les grades et tous les régiments. Il s’agit en d’autres termes d’un carré gréco-latin d’ordre 6 (la combinaison de deux carrés latins, un carré latin pour les régiments, un carré latin pour les grades), problème dont la résolution est impossible. Euler l’avait déjà pressenti à l’époque, sans toutefois donner une démonstration formelle à sa conjecture. Il dira : « Or, après toutes les peines qu’on s’est données pour résoudre ce problème, on a été obligé de reconnaître qu’un tel arrangement est absolument impossible, quoiqu’on ne puisse pas en donner de démonstration rigoureuse. » En 1901, le Français Gaston Tarry démontre l’impossibilité du résultat grâce à une recherche exhaustive des cas et par croisement des résultats. Le lien entre le sudoku et le problème des 36 officiers est la contrainte qui empêche la répétition du même élément dans la grille, tout en arrivant au final à un jeu qui emploie le principe du carré latin (combinaison de deux carrés latins dans le cas du carré gréco-latin, carré latin subdivisé en plusieurs régions dans le cas du sudoku).