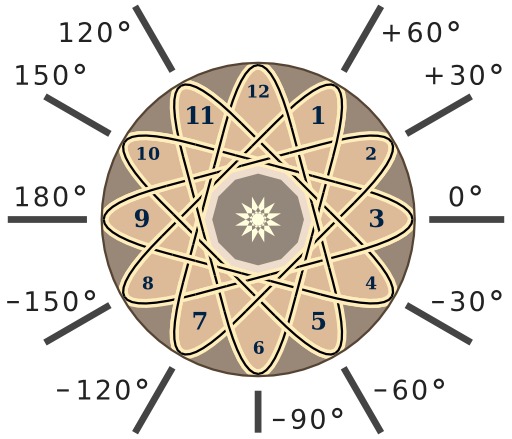
Correspondances heures et angles

Description de la ressource

Douze angles définis modulo 360 degrés correspondent à des temps, définis modulo 12 heures. Par exemple, une aiguille d’horloge a une seule position numérotée zéro ou vingt-quatre, parce que 0 = 24 modulo 12. Cette position correspond à 90 ou –270 degrés modulo 360 degrés. Ainsi nous identifions direction et sens d’une demi-droite ou d’un vecteur en coordonnées polaires, ou l’angle d’une rotation donnée, ou l’argument d’un nombre complexe donné. Le dessin sur le cadran de l’horloge évoque des progressions arithmétiques de raisons 5 ou 7 modulo 12. Par exemple, en tournant dans le sens des aiguilles d’une montre à partir de 1, nous passons par les termes : 1, 6, 11, 4, 9, 2, 7, 12, 5, 10, 3, 8. Cette suite correspond à une progression de raison arithmétique 210 degrés modulo 360 degrés. Si les douze positions d’une aiguille d’horloge sont numérotées dans l’ensemble P de douze éléments, de 1 à 12 modulo 12, et si l’ensemble A est constitué des angles indiqués dans l’image, une bijection B de P sur A peut être définie par B( t ) = 90 – 30 t. Par exemple, B( 12 ) = 90 – 30 × 12 = 90 degrés modulo 360 degrés. L'arithmétique modulaire est un système arithmétique d'entiers modifiés, où les nombres sont « abaissés » lorsqu'ils atteignent une certaine valeur. Donnons comme exemple, l'« arithmétique de l'horloge » qui se réfère à l'« addition » des heures indiquées par la petite aiguille d'une horloge : concrètement, si nous commençons à 9 heures et ajoutons 4 heures, alors plutôt que de terminer à 13 heures (comme dans l'addition normale), nous sommes à 1 heure. De la même manière, si nous commençons à minuit et nous attendons 7 heures trois fois de suite, nous nous retrouvons à 9 heures (au lieu de 21). Fondamentalement, quand nous atteignons 12, nous recommençons à zéro ; nous travaillons modulo 12. Pour reprendre l'exemple précédent, on dit que 9 et 21 sont congrus modulo 12. Les nombres 9 ; 21 ; 33 ; 45 ; etc. sont considérés comme égaux lorsqu'on travaille modulo 12. Pour généraliser, nous pouvons facilement imaginer une horloge qui contient un nombre arbitraire d'heures, et faire des calculs avec un nouveau modulo.

Détails de la ressource

• Déposé par : Anne-Marie Lesca, le 2012-12-28
• Auteur : Baelde
• Origine : http://commons.wikimedia.org/wiki/File:Academ_Bijection_between_angles_and_12_positions_of_a_clock_hand.svg
• Licence : cc-by-sa
• Format : image/svg+xml
• Type : Dessins et plans
• Collection :
• Description ScolomFR : http://data.abuledu.org/LOM/doc0000006230.xml

Téléchargement

512 - 1024 - Fichier Original - Source + Métadonnées SCOLOMFR

Relations et mots clés

Dessins et plans, Calcul, Horloges et montres, Arithmétique, Aiguilles (horlogerie), Arithmétique modulaire