Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Buste de Pythagore
Buste de Pythagore de Samos. Copie romaine de l'original grec. Musée du Capitole à Rome.
Euclide et Pythagore ou la géométrie et l'arithmétique
Euclide et Pythagore ou la géométrie et l'arithmétique (représentation au XVème siècle)
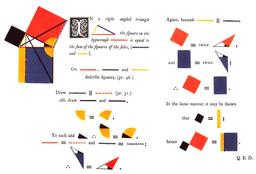
Le théorème de Pythagore
Démonstration du théorème : dans un triangle rectangle, le carré de l'hypothénuse est égal à la somme des carrés des deux côtés.
Margarita Philosophica - Arithmetica, 1508
Fragment d'une gravure sur bois (Grégoire Reisch, 1508) : l'Arithmétique présente un concours entre Boèce (Boetius) et Pythagoras (Pythagore). Ce dernier, manipulant un abaque antique (genre de boulier) peu pratique, est présenté fort embarrassé face à Boèce réjoui qui, ayant usé du calcul décimal et des chiffres indo-arabes, semble avoir terminé.
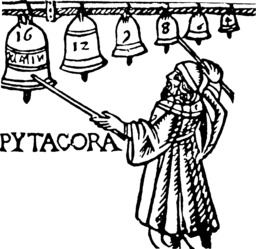
Pythagoras with bells
Fragment de gravure sur bois tiré de la "Theorica musicae" de Franchino Gaffurio, 1492