Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres non-rationnels, Nombres transcendants, Pi (le nombre)
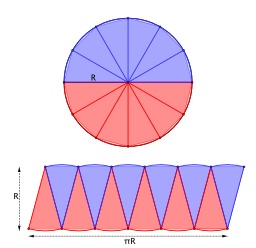
Calcul de l'aire du cercle avec Géogébra
Calcul de l'aire du cercle avec Géogébra : rayon x demi-circonférence. On déduit d’une propriété analogue pour les polygones réguliers que l’aire d’un cercle égale son demi-périmètre multiplié par son rayon. le périmètre du polygone est à peu près 2πr alors qu’en redistribuant les triangles formés on remarque que son aire est à peu près πr2. Pour formaliser le « à peu près » il faudrait faire tendre le nombre de côtés du polygone vers l’infini, ce qui illustre déjà la nature « analytique » de π.
Dessins et plans, Cube, Carré, Géométrie des nombres, Gnomonique, Abu Bakr Muhammad ibn al-Hasan al- Karaji (....-1019 ?)
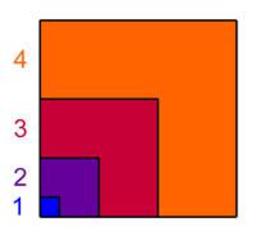
Carré d'un nombre triangulaire
Démonstration géométrique de la formule donnant le carré d'un nombre triangulaire, égal à la somme des premiers cubes parfaits : le carré du nième nombre triangulaire est égal à la somme des n premiers cubes. L'illustration géométrique permet de se convaincre de la véracité de ses propositions. L'aire de la zone orange de la figure est appelée nombre gnomonique. Elle est constituée de deux rectangles de base 4 et de côté le nombre triangulaire d'indice 4, c'est-à-dire 10. Ces deux rectangles se recoupent sur un carré de côté 4, on en déduit que l'aire orange est égale à 5 x 4 x 4 - 4 x 4, ou encore 43. Ce raisonnement est valable sur chaque nombre gnomonique, l'aire du carré de côté le nombre triangulaire d'indice 4 est égal la somme des 4 premiers cubes. De cette démonstration d'Al-Karaji, on déduit la première proposition.
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres transcendants, Pi (le nombre)
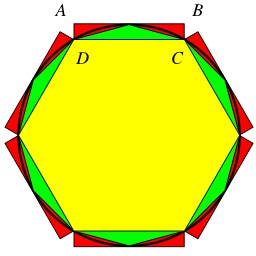
Encadrement de PI par Liu Hui
Représentation de l'encadrement de π par Liu Hui. Si les calculs pratiques peuvent se faire avec une bonne précision en utilisant la valeur 3,14 comme approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416.
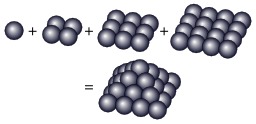
Nombre pyramidal carré 30
Représentation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16.
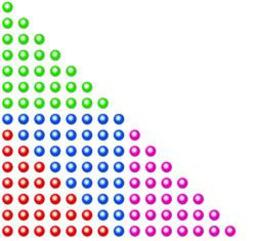
Nombres triangulaires
Somme de quatre nombres triangulaires (pair) : le nombre triangulaire d'indice n est somme de quatre nombres triangulaires. Ceci est vrai quelle que soit la parité de l'indice n. En effet, u14 est la somme de trois fois u7 et de u6 et u15 est la somme trois fois u7 et de u8.
Dessins et plans, Nombres cardinaux, Chiffres, Imagerie (psychologie), Images mentales, Jeux arithmétiques, Géométrie des nombres
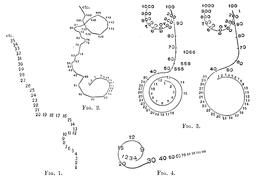
Représentations linéaires de nombres
Plusieurs exemples de représentations linéaires de nombres, 1892-1893. Source : Popular Science Monthly, Volume 42, "Number forms", par G. T. W. Patrick, professeur de philosophie à l'université d'Iowa.
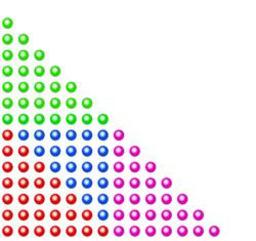
Somme de huit nombres triangulaires
La somme de huit fois un nombre triangulaire et de un est un carré parfait.
Dessins et plans, Carré, Surfaces (mathématiques) -- Volumes, Géométrie des nombres, Johann Faulhaber (1580-1635), Pyramides (géométrie)
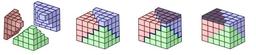
Somme des carrés
Un exemple de preuve sans mots à propos de la somme des premiers carrés : chacune des trois pyramides a pour volume la somme des carrés de 1 à n (n=4 dans cette illustration) ; le parallélépipède final est de côtés n, n+1 et n+1/2. Ce résultat se généralise pour la somme des n premières puissances strictement positives. Cette somme porte le nom de formule de Faulhaber. Johann Faulhaber (1580-1635) est un mathématicien allemand qui collabora avec Kepler.