Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Chiffres, Losanges, Dessin géométrique, As (cartes à jouer), Carreau (cartes à jouer), Carreaux (cartes à jouer)
As de carreau
Schéma d'un as de carreau. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "1".
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Losanges, Dessin géométrique, As (cartes à jouer), Carreaux (cartes à jouer)
As de carreau
L'as de carreau a pour valeur l'as et pour enseigne le carreau. En abrégé, il est noté "1♦", plus rarement "A♦" comme ici. De façon générale, l'as de carreau peut être la plus forte carte des carreaux, suivant immédiatement le roi de carreau, ou la plus petite, précédant le deux de carreau. L'élément principal de la carte est un losange, situé en son centre, indiquant à la fois sa valeur et son enseigne. Source : http://fr.wikipedia.org/wiki/As_de_carreau
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Coeur, Nombres, Chiffres, As (cartes à jouer)
As de coeur
Schéma d'un as de cœur. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "1".
As de coeur
Schéma d'un as de cœur. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "A".
Dessins et plans, Cartes à jouer, Jeux de cartes, noir, Jeux mathématiques, Chiffres, Iconographie, As (cartes à jouer)
As de pique
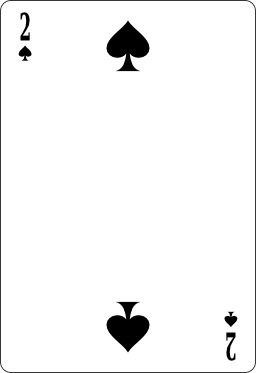
As de pique : de nombreux jeux faisant de pique l'enseigne la plus forte (par exemple au bridge), l'as de pique peut être considéré comme la plus forte de toutes les cartes. C'est ce qui explique que dans les jeux de cartes thématiques, cette carte corresponde à ce qui est vu comme le plus important. L'as de pique et le symbole du pique font partie de l'iconographie associée aux mouvements punk, punk hardcore et hard rock. Source : http://fr.wikipedia.org/wiki/As_de_pique
Dessins et plans, Cartes à jouer, noir, Jeux mathématiques, As (cartes à jouer), Trèfles (cartes à jouer)
As de trèfle
Schéma d'un as de trèfle. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "1" au lieu d'un "A". L'as de trèfle a pour valeur l'as et pour enseigne le trèfle. En abrégé, il est noté "1♣", plus rarement "A♣". Source : http://fr.wikipedia.org/wiki/As_de_tr%C3%A8fle L'as de trèfle fait partie des jeux de cartes occidentaux traditionnels. En particulier, on la retrouve dans les jeux de 32 cartes, de 52 cartes et de tarot. De façon générale, l'as de trèfle peut être la plus forte carte des trèfles, suivant immédiatement le roi de trèfle, ou la plus petite, précédant le deux de trèfle.
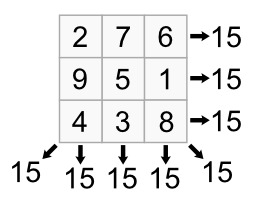
Carré magique
Carré magique normal d’ordre 3 et de constante magique 15. En mathématiques, un carré magique d’ordre n est composé de n^{2} nombres entiers, écrits sous la forme d’un tableau carré. Ces nombres sont disposés de sorte que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales. On nomme alors constante magique (et parfois densité) la valeur de ces sommes.
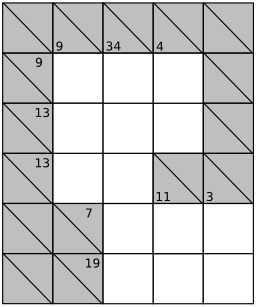
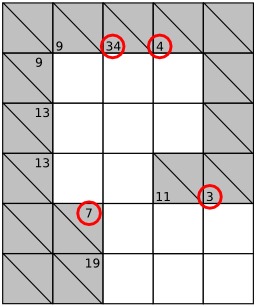
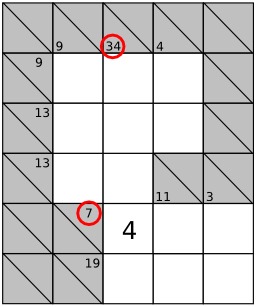
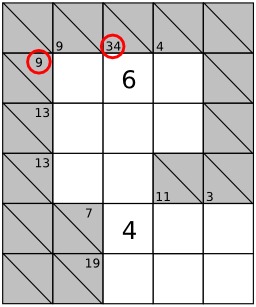
Dessins et plans, Calcul, Jeux mathématiques, Influence japonaise, Kakuro, Combinaisons (mathématiques), Jeux logiques
Combinaisons de nombres pour le jeu japonais du kakuro - 1
Combinaisons de nombres pour le jeu japonais du kakuro : possibilités de décompositions de sommes de nombres différents de 3 à 24.
Combinaisons de nombres pour le jeu japonais du kakuro - 2
Combinaisons de nombres pour le jeu japonais du kakuro : possibilités de décompositions de sommes de nombres différents de 25 à 45.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Claude-Gaspard Bachet (1581-1638)
Construction d'un carré magique - 1
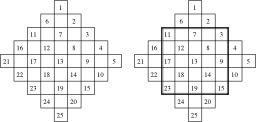
Construction d'un carré magique 5x5, méthode de Méziriac : Premières étapes de construction d'un carré magique d'ordre 5. Chaque diagonale allant de gauche à droite comporte un entier unique en ordre croissant. Ensuite, le contour du carré magique final est esquissé.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Claude-Gaspard Bachet (1581-1638)
Construction d'un carré magique - 2
Dernières étapes de la construction d'un carré magique 5x5 selon la méthode de Méziriac.
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
Construction d'un carré magique par la méthode du losange - 1
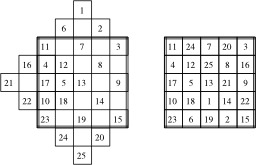
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
Construction d'un carré magique par la méthode du losange - 2
Un carré magique 5x5 construit selon la méthode du losange proposée par John Horton Conway : Le résultat final est un carré magique dont la constante est 65.
Dessins et plans, Jeux mathématiques, Mathématiciens, Carrés magiques, Siam, Simon de La Loubère (1643-1729)
Construction d'un carré magique selon la méthode siamoise
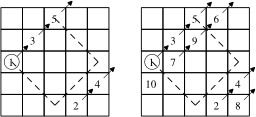
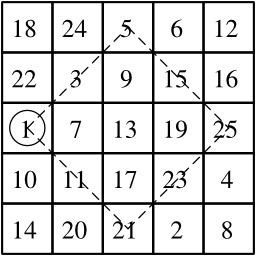
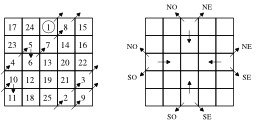
Un carré magique d'ordre 5 avec un carré adjacent montrant des directions : construction d'un carré magique d'ordre impair selon la méthode siamoise. Dans cet exemple, le carré est rempli selon les diagonales nord-est (NE), mais elles pourraient être parallèles à sud-est (SE), à sud-ouest (SO) ou à nord-ouest (NO). 1) Placer le 1 tel que montré. 2) Décaler d'une case vers la droite puis d'une case vers le haut pour le 2, et ainsi de suite pour le 3, puis le 4, etc. 3) Si la pointe de la flèche sort du carré, revenir de l'autre côté, comme si le carré était enroulé sur un tore. 4) Si la prochaine case est occupée, décaler d'une case vers le bas. La méthode siamoise a été introduite en France par Simon de La Loubère en 1688 alors qu'il revenait de son ambassade au Siam. Source : http://fr.wikipedia.org/wiki/Carr%C3%A9_magique_%28math%C3%A9matiques%29.
Construction de carrés magiques, nombres pairs
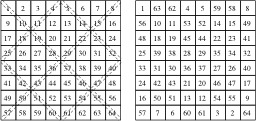
Construction d'un carré magique 8x8 selon la méthode des permutations relativement aux diagonales des sous-damiers 4x4. Dans le carré de gauche, les nombres naturels sont inscrits dans l'ordre. De plus, les diagonales principales de chaque sous-damier 4x4 sont recouvertes de lignes en pointillés. À droite, le carré final, magique, est inscrit. Chaque nombre qui n'était pas recouvert par une ligne en pointillés a été remplacé par son complément à (82 + 1) = 65.
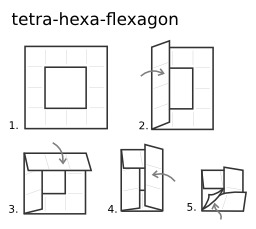
Construction et manipulation d'un hexahexaflexagone
Construction et manipulation d'un hexahexaflexagone en huit étapes.
Photographie, Couleurs, Arithmétique, Jeux mathématiques, Matériel didactique, Quatre (le nombre), Dix-huit (le nombre), Dix (le nombre), Georges Cuisenaire (1891-1975), Méthodes d'apprentissage
Construire dix avec les réglettes cuisenaire
Construire dix avec dix-huit réglettes cuisenaire de quatre couleurs différentes
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
Cordes de Motzkin entre cinq points sur un cercle
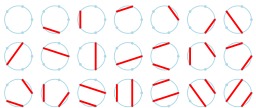
Vingt-une cordes de Motzkin (qui ne se coupent pas) entre cinq points sur un cercle.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
Cordes de Motzkin entre quatre points sur un cercle
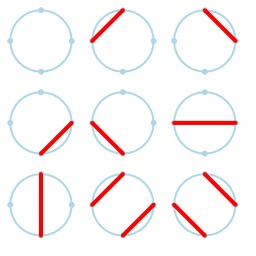
Cordes de Motzkin sur un cercle : les neuf manières de dessiner des cordes qui ne se coupent pas entre quatre points d'un cercle. Le nombre de Motzkin est le nombre de façons de choisir des cordes ne se coupant pas, parmi les cordes reliant n points disposés sur un cercle. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
Dessins et plans, Géométrie, Jeux mathématiques, Jeux de logique, Mathématiciens, Devinettes et énigmes, Casse-tête logique, Énigmes mathématiques, Henry Dudeney (1857-1930)
Enigme des 3 maisons
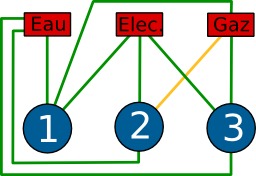
Enigme des trois maisons : Une solution généralement non admise dans l'énigme des trois maisons puisque les canalisations de gaz et d'électricité se croisent. Enigme posée en 1917 par Henry Dudeney (1857-1930) en ces termes : "Un lotissement de trois maisons doit être équipé d'eau, de gaz et d'électricité. La règlementation interdit de croiser les canalisations pour des raisons de sécurité. Comment faut-il faire ?"
Photographie, Jeux mathématiques, Diamants, Jeux de ficelles, Jeux de ficelle, Osage (Indiens) -- Art, Osages (Indiens)
Figure du jeu de ficelle des deux diamants
Jeu indien Osage de ficelle des deux diamants : double noeud. Source : Caroline Furness Jayne, String Figures and How to Make Them, 1962, page 30.
Photographie, Médecins, Jeux mathématiques, Noeuds et épissures, Écrivains grecs anciens, Jeux de ficelles, Jeux de ficelle
Figure grecque au jeu de ficelle
Noeud coulant appelé "Plinthios Brokhos", inventé par Heraklas, un médecin grec du Ier siècle ap. J.-C., essai sur les nœuds et les nœuds coulants, qui pourraient être utiles aux docteurs, ici pour réduire une fracture du maxillaire. Source : Cyrus Day, éQuipus and Witches' Knots".
Flexagone
Hexahexaflexagone. Le flexagone est un objet topologique issu du ruban de Moebius, construit le plus souvent à l’aide d’une bande de papier pliée. Les préfixes que l’on peut ajouter au nom indiquent le nombre de faces différentes du flexagone puis son nombre de côtés. L'hexahexaflexagone a la forme d'un hexagone et possède six faces différentes. C’est une forme complexe du flexagone, fabriquée à partir d’une bande de papier de 18 triangles équilatéraux. Celle-ci est repliée sur elle-même de façon à avoir la longueur de 9 triangles, puis est ensuite pliée comme un trihexaflexgone. Source : http://fr.wikipedia.org/wiki/Flexagone
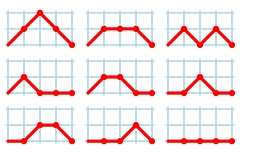
Interprétation du nombre de Motzkin pour quatre pas
Neuf chemins de Motzkin de (0, 0) à (4, 0), pour 4 pas en ne faisant que des pas Nord-Est, Est et Sud-Est. Les chemins sont en bijection avec les arbres. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
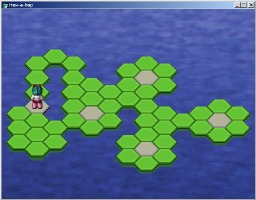
Jeu d'hexagones Hex-a-hop
Jeu de puzzle avec hexagones, créé par Tom Beaumont. Le joueur fait avancer un personnage qui doit détruire tous les hexagones verts en sautant dessus. Les hexagones gris sont des point sûrs, sur lesquels il est possible de passer indéfiniment.