Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Calcul, Carré, Jeux mathématiques, Dominos (jeu), Matériel didactique, Vulgarisation scientifique, Écrivains russes pour la jeunesse, Matériel pédagogique, Intellectuels russes, Yakov Perelman (1882-1942)
Jeu mathématique avec des dominos
Un des carrés possibles du jeu de Yakov Perelman (1882-1942), professeur russe : quatre dominos formant un carré sont disposés de façon à ce que le nombre de points de chacun des cotés soit identique.
Photographie, Géométrie, Jeux mathématiques, Jeux d'extérieur, Géants, Montréal (Canada), Tangram, Jeux de plein air
Jeux d'échecs et de tangram à Montréal
Réalisation de tangrams et jeux d'échecs géants, place Émilie-Gamelin, Montréal
Photographie, Géométrie, Échiquiers, Jeux mathématiques, Jeux d'extérieur, Montréal (Canada), Tangram, Jeux d'échecs, Jeux de plein air
Jeux de tangram de rue à Montréal
Jeux de tangram et jeux d'échecs en plein air, place Émilie-Gamelin, Montréal.
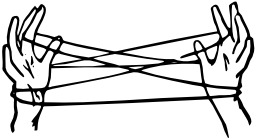
Le berceau du chat en jeu de ficelle
Le berceau du chat, en jeu de ficelle, par Clarence Squareman (1916), "My Book of Indoor Games" (Gutenberg).
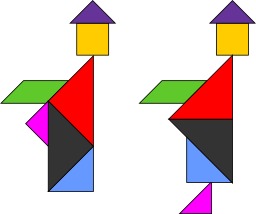
Le tangram des deux moines
Tangram du paradoxe des deux moines : même nombre de pièces mais disposées différemment.
Le tangram des trois vases
Le paradoxe du tangram magique des trois vases, par Sam Loyd, Eighth Book of Tan (1903).
Photographie, Jeux mathématiques, Craie, Numération, Marelles, Chinois (langue), Jeux de plein air, Dix (le nombre), Marelle à cloche pied
Marelle à dix cases en chinois
Marelle à dix cases en chinois, dessinée à la craie : cases en blanc, numéros en couleur.
Dessins et plans, Jeux mathématiques, Jeux d'extérieur, Anglais (langue), Numération, Marelles, Dix (le nombre), Marelle à cloche pied
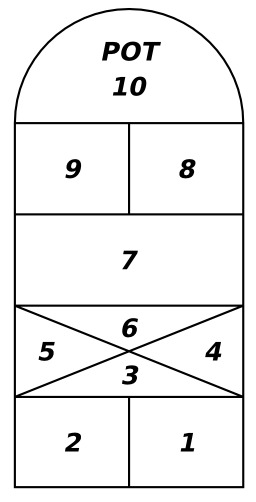
Marelle américaine à dix cases
Marelle américaine à dix cases et "Pot" comme ciel à la dixième case, in D. C. Beard, "The Outdoor Handy Book: For the Playground, Field, and Forest", 1900 : "Hopscotch court", p. 357, fig. 294.
Photographie, Jeux mathématiques, Jeux d'extérieur, Anglais (langue), Numération, Six (le nombre), Marelles, Marelle à cloche pied
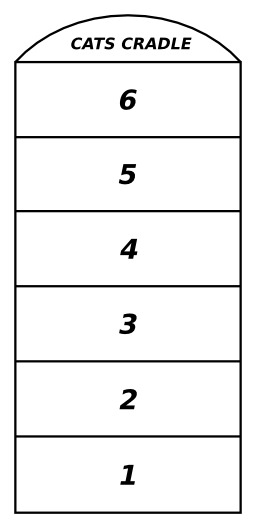
Marelle anglaise à six cases
Marelle anglaise à six cases et "Cat's cradle" comme ciel, in D. C. Beard, "The Outdoor Handy Book: For the Playground, Field, and Forest", 1900 : "Hopscotch court", p. 356, fig. 291.
Photographie, Vie en banlieue, Jeux mathématiques, Jeux d'extérieur, Rues, Craie, Banlieues, Numération, Nu-pieds (sandales), Sandales, Marelles, Jeux de plein air, Art dans la rue, Photographie de rue, Marelle à cloche pied
Marelle interminable dans la rue
Marelle interminable dans la rue dessinée à la craie par deux enfants pieds-nus.
Photographie, Art et sciences, Jeux mathématiques, Expositions, Expositions -- Appareils et matériel, Applications (mathématiques), Expositions -- Aspect social, Expositions scolaires
Matériel d'exposition mathématique
Matériel d'exposition mathématique, Mathematikum, Cap Sciences à Bordeaux, septembre 2011.
Dessins et plans, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Collages (art)
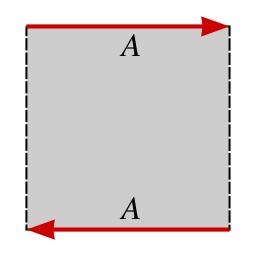
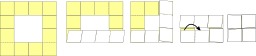
Montage d'un ruban de Möbius
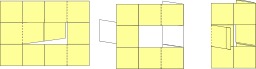
Schéma de montage d'un ruban de Möbius : recoller les deux flèches en respectant le sens.
Dessins et plans, Jeux mathématiques, Jeux de logique, Grilles, Influence japonaise, Kakuro, Mots-croisés
Mots-croisés japonais
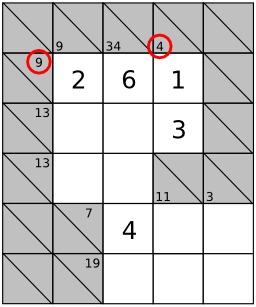
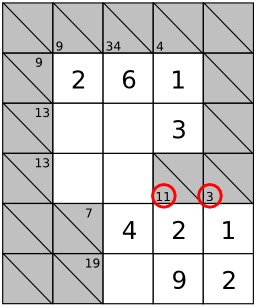
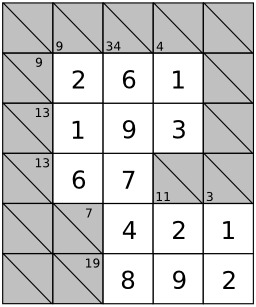
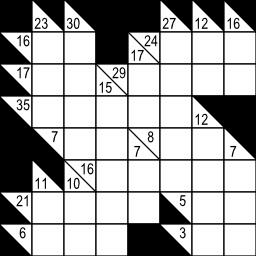
Grille de Kakuro avec solution, jeu de mots-croisés japonais. Outre la ligne du haut et la colonne de gauche, entièrement noires, la grille, telle une grille de mots-croisés, est divisée en « mots » horizontaux ou verticaux par les cases noires. Les cases noires elles-mêmes sont divisées en deux par une diagonale allant du coin en haut à gauche au coin en bas à droite, de sorte que le "mot" à sa droite et le "mot" au-dessous puissent être définis dans la même case. L'objectif du jeu est de remplir les cases vides (blanches) avec des chiffres entre 1 et 9 de sorte que la somme de tous les chiffres d'un nombre soit égale au nombre inscrit dans la case remplie (noire) définissant le nombre, et qu'un nombre ne puisse pas contenir deux fois le même chiffre. Cette dernière règle est celle qui rend possible la création de grilles à solution unique. Source : http://fr.wikipedia.org/wiki/Kakuro.
Multiplication de deux carrés magiques - 1
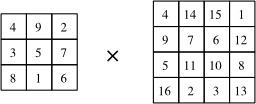
Multiplication de deux carrés magiques : Soit à effectuer le « produit » de ces deux carrés magiques, un de 3x3 et l'autre de 4x4. Le carré magique final sera de 12x12. Le « produit » de deux carrés magiques crée un carré magique d'ordre supérieur aux deux multiplicandes. Ce produit s'effectue ainsi. Soit les carrés magiques M et N : 1) Le carré final sera d'ordre MxN ; 2) Diviser le damier final en NxN sous-damiers de MxM cases ; 3) Dans le carré N, réduire de 1 la valeur de tous les nombres ; 4) Multiplier ces valeurs réduites par M × M. Les résultats sont reportés dans les cases de chaque sous-damier correspondant du carré final ; 5) Les cases du carré M sont additionnées NxN fois aux cases du damier final. Source : http://fr.wikipedia.org/wiki/Carr%C3%A9_magique_%28math%C3%A9matiques%29.
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
Multiplication de deux carrés magiques - 2
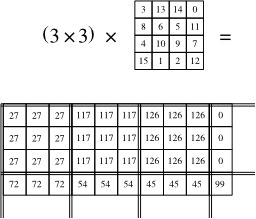
Deuxième étape de la multiplication des deux carrés magiques (3 et 4) : Le carré magique de 3x3 est remplacé par le produit (3 × 3), alors que chaque nombre du carré 4x4 est diminué de 1. Le damier final, de taille 12x12, est divisé en 4x4 sous-damiers, chacun ayant 3x3 cases. Chacune de ses cases s'obtient en multipliant (3 × 3) par l'une des cases du carré magique 4x4 « diminué ». Par exemple, 117 est le produit de 3 × 3 × 13. Ce carré est magique, mais n'est pas normal. La prochaine étape va « corriger » cette « anomalie ».
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
Multiplication de deux carrés magiques - 3
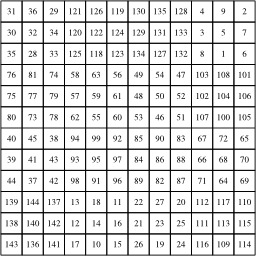
Multiplication de deux carrés magiques, dernière étape : Après 4x4 additions du carré 3x3, le carré final est magique et normal.
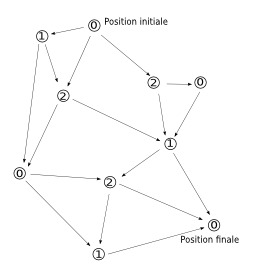
Nombres de Grundy
Nombres de Grundy (ou nimbers) attribués à chaque position d'un graphe symbolisant un jeu de Nim.
Dessins et plans, Géométrie, Jeux mathématiques, Pavages (mathématiques), Mathématiciens, Tuiles, Divertissements mathématiques
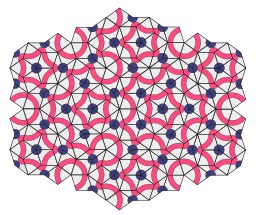
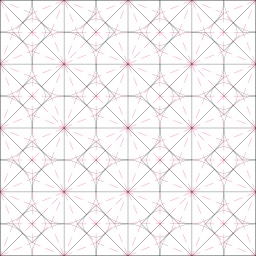
Pavage de Penrose avec tuiles apériodiques
Pavage de Penrose réalisé avec deux tuiles apériodiques. Roger Penrose est un mathématicien anglais. Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement. Plus généralement toute portion finie du pavage, aussi grande soit-elle, se répète infiniment dans le pavage. Les pavages de Penrose ne seraient restés qu'un joli divertissement mathématique si n'avaient été découverts, en 1984, des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux. Les pavages non périodiques, en particulier ceux de Penrose, s'avérèrent alors un modèle plausible de ces étranges matériaux. Cette découverte illustra à nouveau ce que Roger Penrose lui-même avait déjà remarqué en 1973, à propos d’un sujet de relativité générale : « On ne sait jamais vraiment quand on perd son temps ». Source : http://fr.wikipedia.org/wiki/Pavage_de_Penrose.
Dessins et plans, Géométrie, Jeux mathématiques, Oursins, Origami, Pliages en papier, Napperons individuels, Sets de table
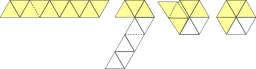
Pliage de napperon en origami
Pliage de napperon en origami, à partir des recherches de J. Lang de pliages pour l'oursin. Source : http://en.wikipedia.org/wiki/Napkin_folding_problem
Dessins et plans, Géométrie, Cube, Jeux mathématiques, Origami, Pliages en papier, Racines numériques, Racines d'un nombre
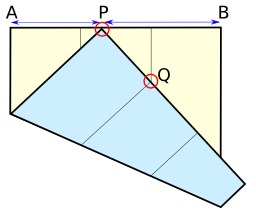
Racine cubique de 2 et origami
Doubler le volume d'un cube : PB/PA = racine cubique de 2. Comment construire la racine cubique de 2 par pliage d'origami : construction par Peter Messer, Problème 1054, Crux Mathematicorum, Vol. 12, No. 10, 1986, pp. 284-285.
Photographie, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Pliages en papier, Mathématiques récréatives, Ferdinand Möbius (1790-1868)
Ruban de Moebius
Ruban de Moebius construit à partir d'une bande de papier, un ruban adhésif retenant les deux bouts. Il est facile de visualiser la bande de Möbius dans l'espace : un modèle simple se réalise en faisant subir une torsion d'un demi-tour à une longue bande de papier, puis en collant les deux extrémités. En topologie, le ruban de Möbius (aussi appelé bande de Möbius ou boucle de Möbius) est une surface compacte dont le bord est homéomorphe à un cercle. Autrement dit, il ne possède qu'une seule face contrairement à un ruban classique qui en possède deux. Elle a la particularité d'être réglée et non-orientable. Source : http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius.