Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
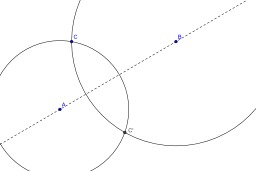
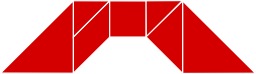
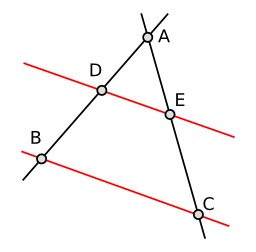
Symétrique d'un point par rapport à une droite
Construction au compas seul du symétrique d'un point par rapport à une droite. Le symétrique du point C par rapport à la droite (AB) est le point d'intersection des cercles de centres A et B et passant par C. Dans la construction la droite (AB) est tracée en pointillés pour permettre de suivre le raisonnement mais elle ne sert pas en tant que telle dans la construction. En géométrie classique plane, le théorème de Mohr Mascheroni, démontré par Georg Mohr en 1672 et par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas seul (sauf le tracé effectif des droites). Est considéré comme constructible tout point d'intersection de deux cercles dont les centres sont des points déjà construits et dont les rayons sont des distances entre des points déjà construits.
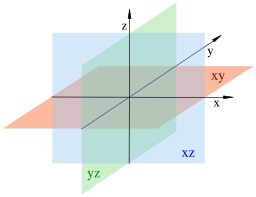
Système de coordonnées dans l'espace
En géométrie analytique, tout point du plan ou de l'espace est « repéré », c'est-à-dire qu'on lui associe un couple (dans le plan) ou un triplet (dans l'espace) de nombres.
Photographie, Géométrie, Topographie, Théodolites, Topographie -- Instruments, Restitution (topographie), Appareils de, Tachéomètres
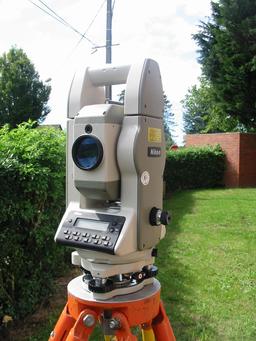
Tachéomètre
Théodolite DTM-A20 (face arrière - cercle à gauche) : Depuis les années 1950 et 1960, les techniques de relevés topographiques évoluent. Avec l'invention des distancemètres électroniques, le théodolite électronique ou le tachéomètre, permettent à la fois de mesurer les distances et les angles. Jusque là, la mesure des distances se faisait à l'aide de rubans gradués (dits chaînes d'arpenteurs) : ces inventions constituent donc une évolution très significative dans le travail des topographes de terrain, presque une révolution.
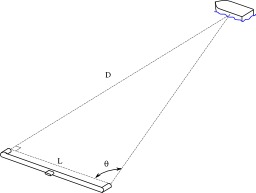
Télémètre à parallaxe
Principe de la mesure au télémètre à parallaxe. La parallaxe est l’incidence du changement de position de l’observateur sur l’observation d’un objet. En d'autres termes, la parallaxe est l'effet du changement de position de l'observateur sur ce qu'il perçoit.
Photographie, Géométrie, Optique -- Instruments, Physique, Optique -- Appareils et matériel, Télémètres optiques
Télémètre optique
Télémètre optique utilisé par les Allemands durant la Seconde Guerre mondiale, 1943. Source : Archives fédérales allemandes. Instrument d'optique indépendant permettant de mesurer la distance d'un objet visé par un système de concordance visuelle à double image donnée par des objectifs dont la grandeur de la base en donnera la précision.
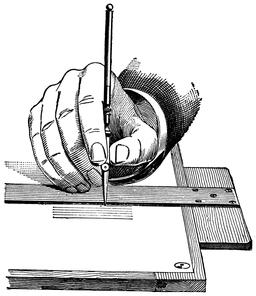
Tenue de crayon à dessin
Tenue de crayon à dessin. Source : “A Textbook on Ornamental Design” (1901)
Photographie, Optique, Géométrie, Cuivre, Topographie, Oberkochen (Allemagne), Théodolites, Topographie -- Instruments
Théodolite ancien
Théodolite datant de 1900, Musée d'optique de Zeiss à Oberkochen en Allemagne. Le théodolite permet de mesurer des angles horizontaux et verticaux.
Théorème d'Apollonius
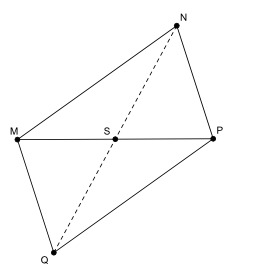
Le théorème de la médiane, ou théorème d'Apollonius, est une relation entre la longueur d'une médiane d'un triangle et la longueur de ses côtés : si S est le centre du parallélogramme, alors 2NS^2 + frac 12 MP^2 = NM^2+NP^2 2NS^2 =frac 12 NM^2+NP^2 NQ^2=NM^2+2NP^2 . Apollonios de Perga ou Apollonius de Perge (en grec ancien Ἀπολλώνιος / Apollốnios, v. 262 – v. 190 av. J.-C.) était un géomètre et astronome grec. Il serait originaire de Pergé (ou Perga, ou encore Pergè actuelle Aksu en Turquie).
Dessins et plans, Géométrie, Carré, Jeux mathématiques, Origami, Pliages en papier, Théorèmes -- Démonstration automatique, Mathématiques japonaises, Nombres rationnels
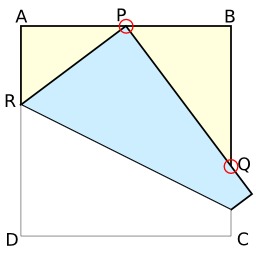
Théorème de Haga et origami
Théorème de Haga et origami : BQ est rationnel si AP l'est, par pliage du sommet d'un carré sur un point P du côté opposé. Source : http://en.wikipedia.org/wiki/Mathematics_of_origami.
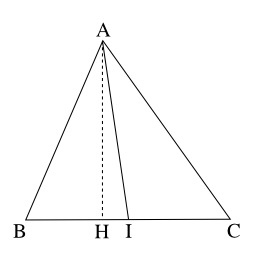
Théorème de la médiane
Médiane et hauteur d'un triangle. Le théorème de la médiane, ou théorème d'Apollonius, est une relation entre la longueur d'une médiane d'un triangle et la longueur de ses côtés. Soit ABC un triangle quelconque, et AI la médiane issue de A. On a alors la relation suivante : AB^2 + AC^2 = 2BI^2 + 2AI^2, Ou encore : AB^2 + AC^2 = {1 over 2} BC^2 + 2AI^2.
Dessins et plans, Géométrie, Disques, Pizzas, Aires (surfaces), Aires (surfaces) -- Mesure, Théorèmes -- Démonstration automatique
Théorème de la pizza
Théorème de la pizza. Source : Carter, Larry & Wagon, Stan (1994a), "Proof without Words: Fair Allocation of a Pizza", Mathematics Magazine 67 (4): 267.
Dessins et plans, Géométrie, Pizzas, Aires (surfaces), Aires (surfaces) -- Mesure, Théorèmes -- Démonstration automatique, Théorèmes -- Preuve automatique
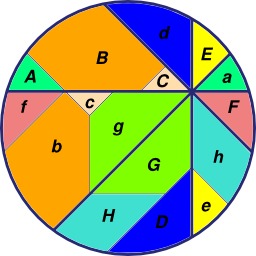
Théorème de la pizza en huit parts
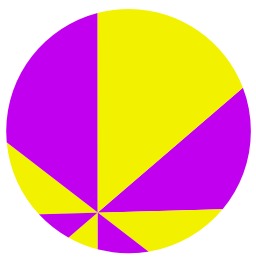
En géométrie euclidienne, le théorème de la pizza donne une égalité ou une inégalité d'aires lors de la partition d'un disque par des droites concourantes. Il porte ce nom en raison d'une forte analogie avec la technique usuelle de découpage d'une pizza. Exemple avec huit parts : aire jaune = aire violette. Source : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_la_pizza.
Dessins et plans, Géométrie, Astronomie, Claude Ptolémée (0100?-0170?), Cercles, Cercles du triangle, Mathématiciens grecs
Théorème de Ptolémée
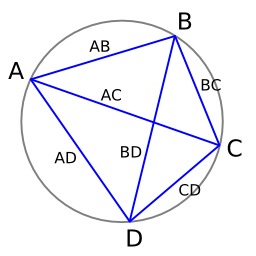
Quadrilatère illustrant le théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne. Il décrit une relation algébrique entre les longueurs des côtés et des diagonales d'un quadrilatère, équivalente à l'inscription du quadrilatère dans un cercle. L'implication directe est attribuée à l'astronome et mathématicien grec Ptolémée, dont il se servit pour ses calculs liés à l'astronomie.
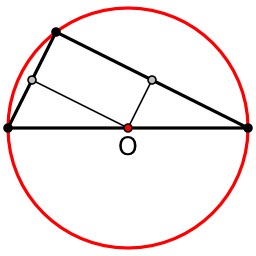
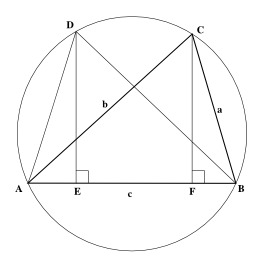
Théorème de Ptolémée
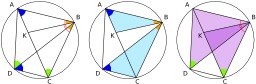
Preuve géométrique du théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne. Il décrit une relation algébrique entre les longueurs des côtés et des diagonales d'un quadrilatère, équivalente à l'inscription du quadrilatère dans un cercle.
Théorème de Stewart
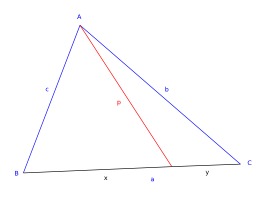
En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane, due au mathématicien Matthew Stewart dans les années 1746 : Théorème — Soit p une cévienne d'un triangle ABC divisant en X le côté a en deux parties x et y. On a alors la relation suivante : acdot (xy+p^{2}) = xcdot b^{2}+ycdot c^{2}. Matthew Stewart est un mathématicien écossais (1717-1785) reconnu comme un mathématicien important après la publication de son "General Theorems", en 1746.
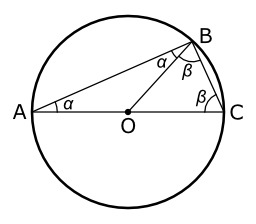
Théorème de Thalès (cercle)
Théorème de Thalès sur le cercle. Le théorème de Thalès sur le cercle est un théorème de géométrie qui affirme qu'un triangle inscrit dans un cercle et dont un côté est un diamètre est un triangle rectangle.
Clip art, Géométrie, Triangle, Angles, Cercle, Philosophes grecs, Philosophes antiques, Thalès, Théorème de
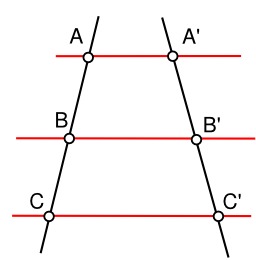
Théorème de Thalès (triangle)
Illustration du théorème de Thalès dans un demi-cercle : propriétés des angles inscrits et complémentaires.
Théorème de Thalès de Milet (triangle)
Illustration du théorème de Thalès : triangles inscrits dans un demi-cercle.
Clip art, Géométrie, Angles, Claude Ptolémée (0100?-0170?), Almageste - Claude Ptolémée (0100?-0170?)
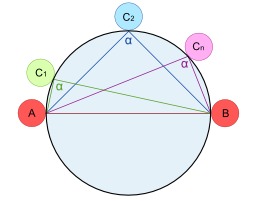
Théorème du cosinus de Ptolémée
Au IIe siècle de notre ère, Ptolémée d’Alexandrie dans son « Almageste », a établi des égalités de rapport équivalentes aux formules d'addition et de soustraction donnant sin(A+B) et cos(A+B). Ptolémée établit une formule équivalente à la formule de l’angle moitié sin^2(A/2)=(1-cos A)/2 et dressa une table de ses résultats.
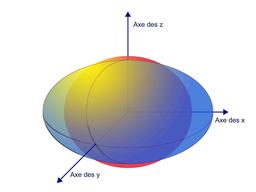
Théorème spectral
Représentation de la sphère unité en dimension trois pour deux distances euclidiennes. La sphère rouge représente la sphère unité pour la première forme, la figure bleue représente la sphère unité pour la deuxième forme dans la mesure où celle-ci est définie positive. La figure bleue est un ellipsoïde dont les axes sont orthogonaux pour la première forme. La distance d'origine est définie par la sphère rouge et celle de la quadrique associée à Ψ, par l'ellipsoïde bleu. Il existe alors une base qui respecte l'orthogonalité des deux formes quadratiques. Si l'orthogonalité est respectée, il n'en est pas de même pour les longueurs. Ainsi, le vecteur unitaire de l'axe des x pour la distance originale (en rouge) est de longueur plus petite pour la nouvelle distance (en bleu), d'où la nécessité d'un coefficient s1 pour passer d'une distance à l'autre.
Dessins et plans, Géométrie, Noeuds et épissures, Entrelacs (arts décoratifs), Topologie combinatoire
Théorie des noeuds
Diagramme d'un nœud torique de type (3,8). La théorie des nœuds est une branche de la topologie qui consiste en l'étude mathématique de bouts de ficelles idéalisés. Elle est donc très proche de la théorie des tresses. Source : http://fr.wikipedia.org/wiki/Th%C3%A9orie_des_n%C5%93uds