Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Géométrie, Lune, Horloges et montres, Étoiles, Aiguilles (horlogerie), Temps -- Mesure
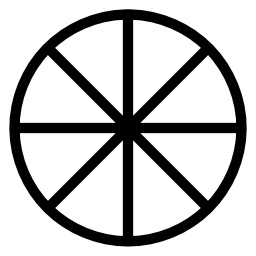
Horloge sans chiffres à Hambourg
Horloge sans chiffres de l'église St. Jacob à Hamburg en Allemagne. L'aiguille des heures se termine par une étoile et celle des minutes par un quartier de lune. Il est 17h23.
Identité remarquable
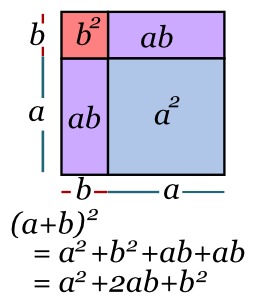
Visualisation géométrique de l'identité remarquable du second degré (a+b)^2 = a^2 + 2ab + b^2,
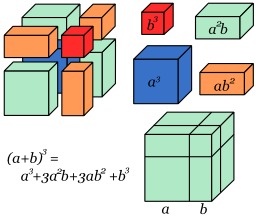
Identité remarquable
Représentation graphique de l’identité remarquable (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3.
Dessins et plans, Géométrie, Équations, Identités remarquables, Équations -- Solutions numériques, Équations algébriques, Équations du second degré
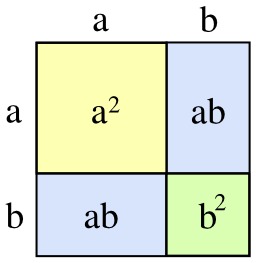
Identité remarquable du second degré
Identité remarquable du second degré : équation (a+b)^2=a^2 + 2ab + b^2. Pour se convaincre de la véracité de la formule, on considère cette figure qui représente un carré. On suppose que la longueur côté du carré jaune est égale à a et celle du carré vert à b. L'aire du grand carré est égale à (a + b)^2. Il existe une autre manière d'exprimer cette aire, elle est la somme des aires jaune, verte et des deux zones bleues. L'aire jaune est égale à a^2 car c'est un carré de côté a, l'aire verte est égale à b^2 et chaque rectangle bleu possède des côtés de longueur a et b, leur aire est égale à ab. Comme il existe deux rectangles bleus, on obtient bien la formule annoncée.
Dessins et plans, Géométrie, Signaux et signalisation, Panneaux à message variable, Signalisation, Agglomération, Chaussées, Trottoirs
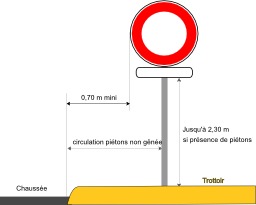
Implantation panneau de signalisation
Caractéristiques d'implantation d'un panneau de signalisation de prescription en agglomération en France.
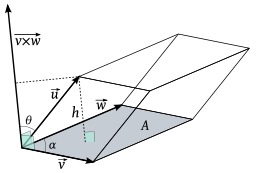
Interprétation géométrique du triple produit scalaire
Interprétation géométrique du triple produit scalaire.
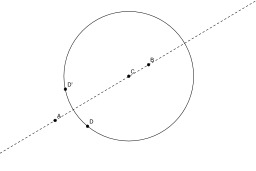
Intersection d'une droite et d'un cercle au compas
Construction au compas seul de l'intersection d'un cercle avec son diamètre : Si la droite (AB) est un diamètre du cercle, et si le point D n'est pas situé sur (AB). On construit de symétrique de D par rapport à (AB). Les deux points à chercher sont les milieux des deux arcs d'extrémités DD'.
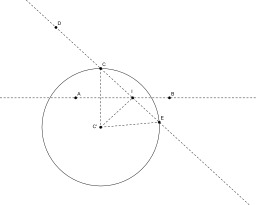
Intersection de deux droites
Construction au compas seul de l'intersection de deux droites (étape 1) : construction du point C' symétrique de C par rapport à (AB) et du point E sur (CD) tel que C'C=C'E.
Photographie, Géométrie, Architecture des jardins, Architecture végétale des jardins, Podensac (Gironde. - région), Sauternes (Gironde), Vignobles, Géométrie de la ligne, Perspective
Jardin dans un vignoble
Photographie des jeux de ligne entre jardin et paysage du vignoble du Sauternais, entre minéral et végétal. Malle à Preignac-33.
Photographie, Géométrie, Couleurs, Jeux éducatifs, Jeux de dés, Jeux de société, Formes (mathématiques)
Jeu de formes géométriques
Jeu de plateau "Fits" : association de formes géométriques de couleur. Jeu créé par Charles B. Phillips et Ronald Wiecek en 1999 et édité par Ravensburger. Pour 2 à 4 joueurs, à partir de 8 ans, pour environ 5 à 15 minutes. Les joueurs cherchent à compléter une planche carrée à l'aide d'éléments géométriques de couleurs différentes le plus vite possible, tout en respectant des règles de placement relatives aux lignes de la planche et aux couleurs. Matériel : 4 planches de jeu, un support de pièces proposant 5 piles de pièces (2 pour chaque taille de triangle et 1 pour les carrés), 80 pièces de 4 couleurs différentes (rouge, jaune, vert et bleu) réparties de la manière suivante : 32 grands triangles, 32 petits triangles, 16 carrés ; et un dé spécial (2 faces "petit triangle", 2 faces "grand triangle", 1 face "carré" et 1 face "main").
Photographie, Géométrie, Jeux mathématiques, Jeux d'extérieur, Géants, Montréal (Canada), Tangram, Jeux de plein air
Jeux d'échecs et de tangram à Montréal
Réalisation de tangrams et jeux d'échecs géants, place Émilie-Gamelin, Montréal
Photographie, Géométrie, Échiquiers, Jeux mathématiques, Jeux d'extérieur, Montréal (Canada), Tangram, Jeux d'échecs, Jeux de plein air
Jeux de tangram de rue à Montréal
Jeux de tangram et jeux d'échecs en plein air, place Émilie-Gamelin, Montréal.
Dessins et plans, Géométrie, Couleurs, Tapis, Carré, Mathématiciens, Savants polonais, Wacław Sierpinski (1882-1969), Fractales
Le carré de Sierpinski
Le tapis de Sierpiński (1916), du nom de Wacław Sierpiński (1882-1969), est une fractale obtenue à partir d'un carré. Le tapis se fabrique en découpant le carré en neuf carrés égaux avec une grille de trois par trois, et en supprimant la pièce centrale, et en appliquant cette procédure indéfiniment aux huit carrés restants.
Le carré qui voulait devenir rond
Le carré qui voulait devenir rond, histoire imaginée par Odysseus pour Noël 2014. 1363 mots. Source : http://odysseuslibre.be/mondelibre/le-carre-qui-voulait-devenir-rond/
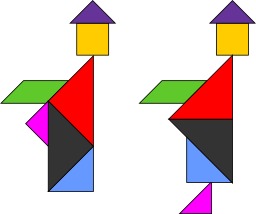
Le tangram des deux moines
Tangram du paradoxe des deux moines : même nombre de pièces mais disposées différemment.
Le tangram des trois vases
Le paradoxe du tangram magique des trois vases, par Sam Loyd, Eighth Book of Tan (1903).
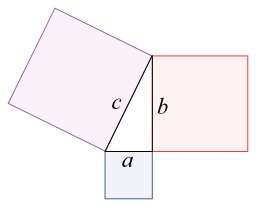
Le théorème de Pythagore
Version géométrique du théorème de Pythagore, le théorème fondamental des espaces euclidiens : la somme des surfaces des deux carrés rose et bleu est égale à la surface du carré violet dont le côté est l'hypothénuse.
Dessins et plans, Géométrie, Ellipses (mathématiques), Cercles, Sections coniques, Hyperboles (mathématiques), Paraboles (mathématiques)
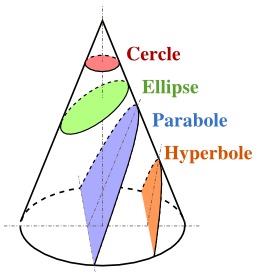
Les quatre sections coniques
Les quatre sections coniques : cercle, ellipse, parabole, hyperbole. Traduction en français Christophe Carina.
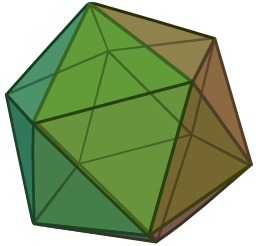
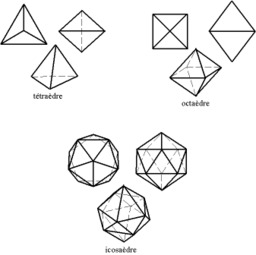
Les trois polyèdres réguliers convexes à faces triangulaires
Plusieurs polyèdres (réguliers ou non) ont des faces triangulaires, comme le tétraèdre, l'octaèdre, l'icosaèdre et le grand icosaèdre. Les polyèdres dont toutes les faces sont des triangles équilatéraux sont appelés deltaèdres.
Dessins et plans, Géométrie, Perspective, Espace (architecture), Espace (art), Géométrie de l'espace, Images tridimensionnelles, Vues perspectives
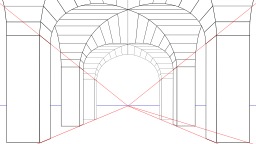
Lois de la perspective
Perspective avec lignes de fuite et point de fuite. La perspective est l'ensemble des lois permettant de représenter sur un plan des figures à trois dimensions. En art, notamment en peinture et en architecture, il faudrait parler des perspectives : diverses méthodes ont été utilisées pour donner l'illusion de la réalité tridimensionnelle.
Dessins et plans, Géométrie, Lune, Étoiles, Cinq (le nombre), Triangle, Polygones, Quatre (le nombre), Turquie
Lune et quatre étoiles turques
Reprise géométrique d'Ay yildiz, le drapeau de la Turquie : lune décroissante et étoile à cinq banches
Mandala de Sable 03
Premier jour de la réalisation d'un mandala de sable "Pour la paix dans le monde", par trois lamas du temple des Mille Bouddhas, à la Tour de la Liberté de Saint-Dié-des-Vosges, les 11, 12 et 13 avril 2008 : le carré et ses quatre portes, le cercle central.
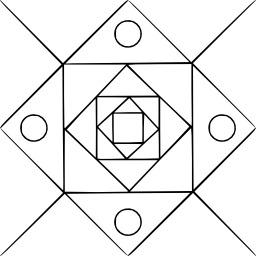
Mandala de Vajradhatu
Mandala de Vajradhatu (boudhisme tibétain) du XIXème siècle : forme de base carrée avec quatre portes d'entrée, contenant un cercle et un centre (symétrie centrale).
Photographie, Géométrie, Léonard de Vinci (1452-1519), Amboise (Indre-et-Loire) -- Manoir du Clos Lucé
Maquette de la sphère de Campanus au Clos Lucé
Maquette de la sphère de Campanus (Septuaginta duarum basium vacuum) dans le jardin du Clos Lucé à Amboise, d'après un dessin de Léonard de Vinci.
Gravure, Géométrie, Albrecht Dürer (1471-1528), Symbolisme dans l'art, Carrés magiques, Attributs (symbolisme), Mélancolie
Mélancolie
Melencolia ou La Melencolia est le nom donné à une gravure sur cuivre d'Albrecht Dürer datée de 1514. Le titre est pris de l'œuvre où il apparaît comme un élément de la composition. Melencolia I est souvent considéré comme faisant partie d'une série, Meisterstiche, comprenant également Le chevalier, la mort et le diable (1513) et Saint Jérôme dans sa cellule (1514). Cette œuvre d'une richesse symbolique exceptionnelle a été l'objet d'un nombre considérable d'études. Source : http://fr.wikipedia.org/wiki/Melencolia_I.
Mesure d'un tour de roue
Relation entre la rotation d'une roue et l'avance d'un véhicule : longueur de l'arc de cercle. En un tour de roue, on avance d'une longueur correspondant au périmètre.
Dessins et plans, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Collages (art)
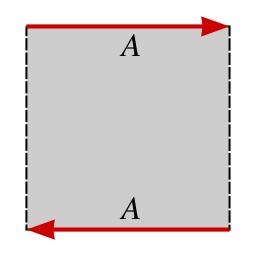
Montage d'un ruban de Möbius
Schéma de montage d'un ruban de Möbius : recoller les deux flèches en respectant le sens.
Photographie, Géométrie, Antiquités gallo-romaines, Octogones, Formes (mathématiques), Mosaïques, Bordeaux (Gironde) -- Musée d'Aquitaine, sylvanus-aquitaine
Mosaïque géométrique de Burdigala
Mosaïque géométrique de Burdigala : motif d'octogone et de huit carrés adjacents.
Photographie, Géométrie, Antiquités gallo-romaines, Bordeaux (Gironde), Mosaïques, Burdigala (ville ancienne), Bordeaux (Gironde) -- Musée d'Aquitaine
Mosaïque géométrique de Burdigala
Mosaïque géométrique de Burdigala, vue d'ensemble, Musée d'Aquitaine, Bordeaux.
Photographie, Afrique, Géométrie, Leyde (Pays-Bas), Art africain, Ghana -- Ethnologie, Pays-Bas (Guillaume II) (1840-1849)
Motifs de l'art Adinkra en 1825
Motifs de l'art Adinkra en 1825 (Ghana). Toile de coton, peinture à partir d'écorce d'arbre, impression à la main ; dimensions : 271 cm de long sur 212 cm de large. Conservé au Musée National d'Ethnologie de Leyde. Source : http://www.volkenkunde.nl/rmv/internet/eain_ghana.html ". Envoyé en 1825 depuis le fort de Saint George d'Elmina (côte de Guinée) au Cabinet Royal de Curiosités de La Hague. Oeuvre probablement réalisée spécialement pour le roi Guillaume I, ce qui expliquerait la présence centrale du blason hollandais.
Nature morte au pot de gingembre en 1912
Nature morte au pot de gingembre en 1912, par Piet Mondrian.
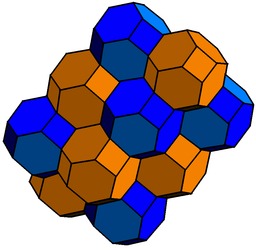
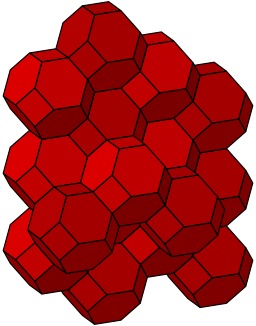
Nids d'abeille partiels
En géométrie, les polyèdres obliques infinis sont une définition étendue des polyèdres, créés par des faces polygonales régulières, et des figures de sommet non planaires. Beaucoup sont directement reliés aux nids d'abeille convexes uniformes, étant la surface polygonale d'un nid d'abeille avec certaines cellules enlevées. En tant que solides, ils sont appelés nids d'abeille partiels et aussi éponges. Ces polyèdres sont aussi appelés pavages hyperboliques parce qu'ils peuvent être regardés comme reliés aux pavages de l'espace hyperbolique qui ont aussi un défaut angulaire négatif.