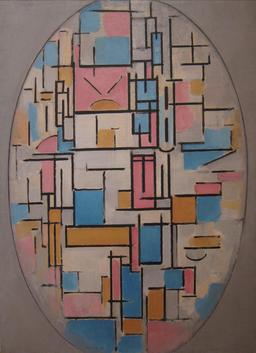Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Apiculture, Alvéoles, Giacomo Filippo Maraldi (1665-1729), Hexagone, Histoire des animaux - Aristote (0384-0322 av. J.-C.), Pappus d'Alexandrie (02..-03..)
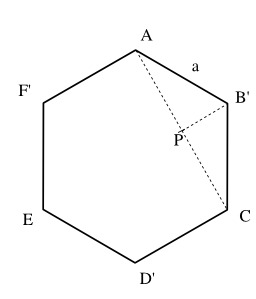
Alvéole hexagonale
Illustration pour alvéole d'abeille. La forme hexagonale des alvéoles fut repérée par Aristote dès le IVe siècle av. J.-C.(Histoire des animaux) puis traitée géométriquement huit siècles plus tard par Pappus, mathématicien grec ; mais ce n’est qu’au XVIIIe siècle que cette forme rhomboïdale fut remarquée. Ainsi, Maraldi, astronome à l’Observatoire de Paris, détermina expérimentalement en 1712 la valeur des angles de ces rhombes, égale à 109° 28′ et 70° 32′.
Photographie, Géométrie, Apiculture, Alvéoles, Gâteaux de cire, René Antoine Ferchault Réaumur (seigneur de, 1683-1757)
Alvéoles d'abeille
Intrigué par la complexité de ces formes, le physicien Réaumur soupçonne les abeilles de construire leur gâteau de cire dans un souci d’économie. Afin de vérifier son hypothèse, il demanda au géomètre allemand König de déterminer quelle était la cellule hexagonale à fond composé de trois rhombes égaux qui pouvait être construite avec le moins de matière possible.
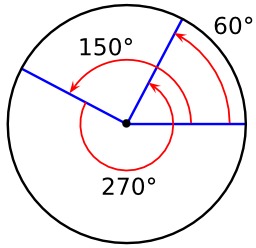
Amplitude (pendule)
Mesure de l'amplitude d'un angle de 90° par un balancier. Le balancier d’une horloge est un élément mobile animé d'un mouvement alternatif de va et vient. Il est horizontal ou circulaire au début et se nomme foliot ou balancier dans les montres actuelles. Il peut aussi prendre la forme d'un pendule, constitué d’une tige verticale, pouvant osciller autour d’un axe horizontal, et comportant un poids à son extrémité basse. Ce poids se présente généralement sous la forme d’un disque bombé, habituellement d’un métal lourd (tel que l’acier), afin de réduire l'influence des forces de résistance de l’air.
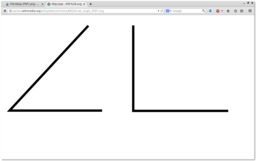
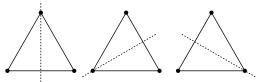
Angle aigu comparé à un angle droit
Angle aigu (à gauche) comparé à un angle droit (à droite), dessin non légendé.
Angle aigu comparé à un angle droit
Angle aigu comparé à un angle droit, traduction en francais als-33.
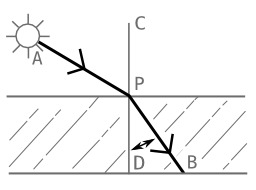
Angle de réfraction
Angle de réfraction : La réfraction, en physique des ondes — notamment en optique, acoustique et sismologie — est un phénomène de déviation d'une onde lorsque sa vitesse change entre deux milieux. La réfraction survient généralement à l'interface entre deux milieux, ou lors d'un changement de densité ou d'impédance du milieu.
Dessins et plans, Géométrie, Barcelone (Espagne), Astronomes, Dunkerque (Nord), Trigonométrie, Jean-Baptiste Delambre (1749-1822), Pierre Méchain (1744-1804), Télémètres
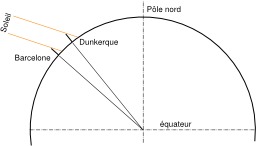
Angle Dunkerque Barcelone
Mesure de l'angle de l'arc de méridien entre Dunkerque (France) et Barcelone (Espagne) en utilisant l'ombre d'un bâton planté à la verticale. Ceci fut fait par des expéditions menées par Delambre et Méchain. Pour mesurer la distance de Dunkerque à Barcelone (qui sont sur un même méridien), on mesura la distance de proche en proche entre des points bien visibles : sommet des églises et des collines. Pour cela, on se place en un point, et on vise l'autre point, selon un principe similaire au télémètre ; la mesure des angles permet de déterminer la distance.
Dessins et plans, Géométrie, Aires (surfaces), Aires (surfaces) -- Mesure, Nombres transcendants, Pi (le nombre), British library -- Manuscrits. Papyrus 10188, Papyrus Bremner-Rhind
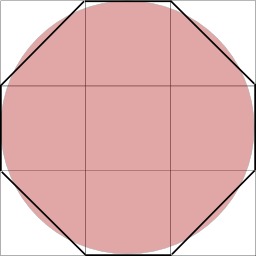
Approximation de PI par Ahmès
Illustration de l'approximation de π (PI) par Ahmès (Égypte). Découvert en 1855, le papyrus de Rhind contient le texte, recopié vers l’an 1650 avant notre ère par le scribe égyptien Ahmès, d’un manuel de problèmes pédagogiques très ancien. On y trouve une méthode pour évaluer l’aire d’un disque en prenant le carré dont le côté est égal au diamètre du disque diminué d’un neuvième. Cette méthode conduit à une évaluation de π de 256/81. Dans l’illustration ci-contre, le disque a pour diamètre 9. L’aire du disque est légèrement supérieure à l’aire de l’octogone irrégulier obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l’aire du disque est alors évaluée à 64 soit l’aire d’un carré de côté 8. Le rapport entre l’aire du disque et le carré du rayon est alors évalué par 64/(9/2)^2, c’est-à-dire 256/81.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
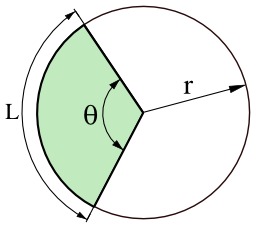
Arc de cercle
Cercle de rayon "r", arc de cercle de longueur "L" soustendu par un angle θ (theta) avec un secteur circulaire de surface "A".
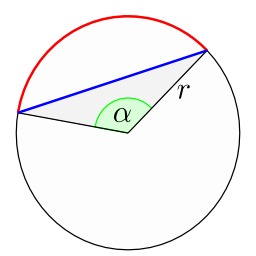
Arc et corde d'un cercle
Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Une corde (en bleu) est un segment de droite dont les extrémités se trouvent sur le cercle. Un arc est une portion de cercle délimitée par deux points (en rouge). Un secteur circulaire est une partie du disque comprise entre deux rayons. Un angle au centre (vert) est un angle formé par deux rayons du cercle.
Dessins et plans, Géométrie, Jouets de papier, Jouets, Origami, Pliages en papier, Avions en papier, Planeurs
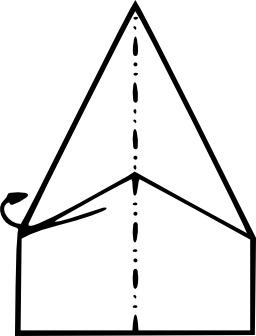
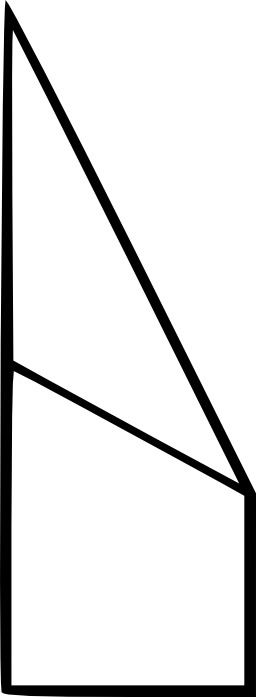
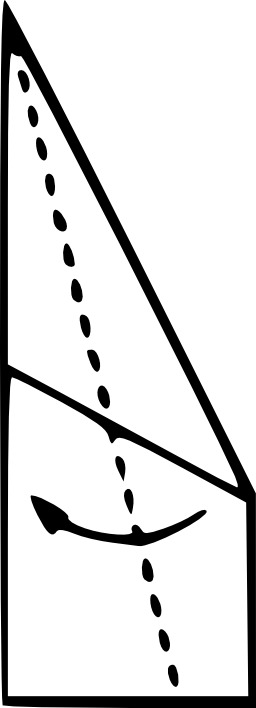
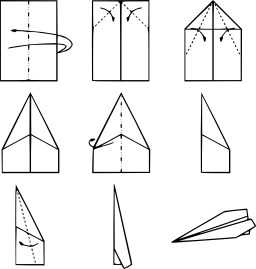
Avion de papier par pliage 10
Neuf étapes de fabrication d'un avion en papier par pliage (origami).
Photographie, Géométrie, Compas, Armoiries, Équerres, Blasons, Architecture, Bas-reliefs, Porto Alegre (Brésil)
Blason universitaire avec compas et équerre
Blason de l'Institut Parobé, Université Fédérale de Rio Grande do Sul au Brésil. Le nom Parobé est un hommage rendu à l'ingénieur João Batista Parobé, responsable de la construction de la ligne de chemin de fer Novo Hamburgo - Canela - Taquara, qui permit l'émergence et l'existence de la future commune à partir de 1903. Les premiers colonisateurs furent essentiellement des Allemands. Source : https://fr.wikipedia.org/wiki/Parob%C3%A9
Dessins et plans, Géométrie, Rubans, Bouteilles, Mathématiciens, Ferdinand Möbius (1790-1868), Felix Klein (1849-1925)
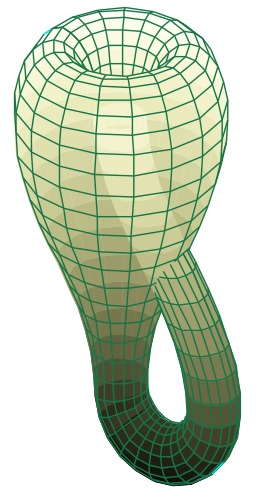
Bouteille de Klein
Vue de la bouteille de Klein dans un espace à trois dimensions. En mathématiques, la bouteille de Klein (prononcé kla.in) est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle il n'est pas possible de définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein (1849-1925). Elle est étroitement liée au ruban de Möbius.
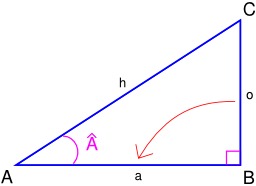
Calcul de la tangente de l'angle A
Représentation géométrique de la tangente dans un triangle rectangle. La tangente d'un angle est le rapport de la longueur du côté opposé à la longueur du côté adjacent :tan(Â) = longueur du côté opposé / longueur du côté adjacent = o/a. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique
Calcul du Cosinus de l'angle A
Représentation géométrique d'un cosinus dans un triangle rectangle : Le cosinus d'un angle est le rapport de la longueur du côté adjacent par la longueur de l'hypoténuse :cos(Â) = longueur de côté adjacent / longueur de l'hypoténuse = a/h. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique
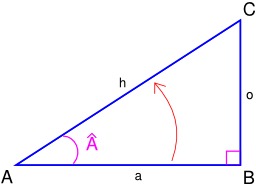
Calcul du Sinus de l'angle A
Représentation géométrique du sinus dans un triangle rectangle. Le sinus d'un angle est le rapport de la longueur du côté opposé par la longueur de l'hypoténuse :sin(Â) = longueur du côté opposé / longueur de l'hypoténuse = o/h. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
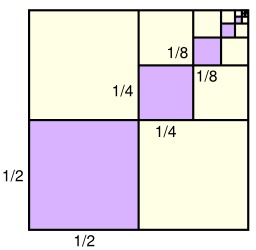
Carrés géométriques
Illustration de l'égalité 1/4 + 1/16 + 1/64 + 1/256 + ⋯ = 1/3 : chacun des carrés violets mesure 1/4 de la surface du grand carré le plus proche (1/2×1/2 = 1/4, 1/4×1/4 = 1/16, etc.). Par ailleurs, la somme des aires des carrés violets est égale à un tiers de la superficie du grand carré.
Dessins et plans, Géométrie, Tapis, Architecture -- Dessins et plans, Symétrie, Tapis persans, Art iranien, Systèmes de quadrillage, Art décoratifs, Tapis -- Cartons
Carton de tapis iranien
Angle d'un plan ("carton") de tapis iranien à formes géométriques, avec indication des couleurs, sur papier quadrillé.
Photographie, Géométrie, Tapis, Croquis (art), Symétrie, Arts décoratifs, Tapis persans, Art iranien, Tapis -- Modèles, Tapis -- Cartons
Cartons de tapis iraniens
Plans ("cartons") de tapis iraniens sur papier quadrillé avec indications de coloriage.
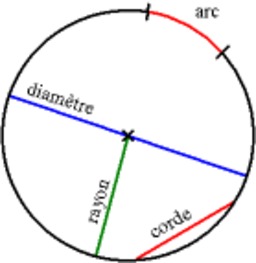
Cercle et son vocabulaire
Définition des termes géométriques concernant le cercle : arc, rayon, diamètre, corde.
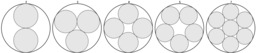
Cercles dans un cercle
Schéma des configurations de 5 cercles avec respectivement 2, 3, 4, 5 et 7 cercles inscrits.
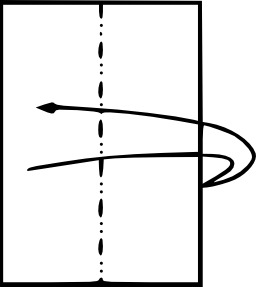
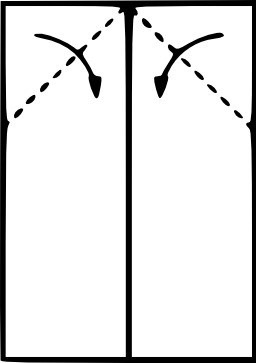
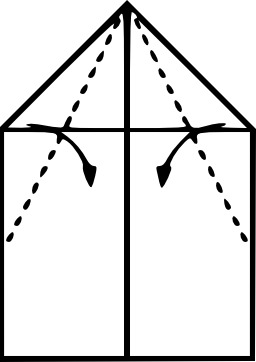
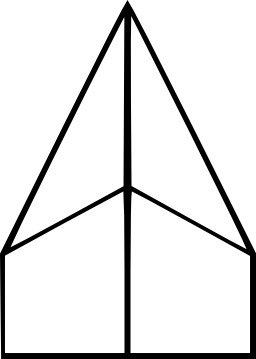
Cinq formes de tentes
Cinq formes de tentes légères : 1. géodésique, 2. dome, 3. tunnel, 4. crête, 5. pyramide. les tentes gonflables : la membrane est conçue pour se tendre sous l'action d'un gaz, celui-ci exerce une pression qui lui donne sa forme. Il s'agit ensuite de lester et de haubaner l'ensemble pour garantir une résistance optimale. Les formes obtenues sont généralement des solides gaussiens facilement concevables avec les logiciels de mise en forme 3D.
Dessins et plans, Géométrie, Bleu, Rouge, Vert, Humour, Lapins, Formes animales dans les arts décoratifs, Formes -- Aspect symbolique, Jeux géométriques
Comment dessiner un lapin
Comment dessiner un lapin avec Inkscape en utilisant trois formes et trois couleurs.
Composé polyédrique de cinq tétraèdres
Composé polyédrique de cinq tétraèdres (Wenninger modèle 25). Un composé polyédrique est un polyèdre qui est lui-même composé de plusieurs autres polyèdres partageant un centre commun, l'analogue tridimensionnel des composés polygonaux tels que l'hexagramme. Enveloppe convexe : Dodécaèdre ; Noyau : Icosaèdre ; Source : http://fr.wikipedia.org/wiki/Compos%C3%A9_poly%C3%A9drique.
Photographie, Géométrie, Illusions d'optique, Art contemporain, Art optique, Art abstrait, Op art, Pécs (Hongrie), Victor Vasarely (1908-1997)
Composition monumentale de Vasarely en Hongrie
Œuvre de Vasarely (1908-1997) devant l'église Pálosok (Pálosok templom), rue János Hunyadi (Hunyadi János utca), à Pécs, en Hongrie. Op art, ou art optique, est une expression utilisée pour décrire certaines pratiques et recherches artistiques faites à partir des années 1960, et qui exploitent la faillibilité de l'œil à travers des illusions ou des jeux optiques. Les œuvres d'op art sont essentiellement abstraites. Les pièces donnent l'impression de mouvement, d'éclat de lumière et de vibration ou de mouvements alternés. Ces sollicitations visuelles placent le corps du spectateur en situation instable, entre plaisir et déplaisir, plongé dans une sensation de vertige proche de certains états d’ivresse légère. Ce phénomène est parfois renforcé par le caractère monumental des pièces, parfois des environnements, voire dans le cas d’art opticocinétique de réelles sources de lumière jaillissant de l’ombre. Source : http://fr.wikipedia.org/wiki/Op_Art
Composition ovale avec plans en couleurs en 1914
Composition ovale avec plans en couleurs en 1914, par Piet Mondrian. Museum of Modern Art (New York).