Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Astronaute en orbite
L'astronaute Stephen K. Robinson, ancré par les pieds au bras Canadarm2 de la Station Spatiale Internationale, participe à la troisiemme session extravehiculaire (EVA) de la mission. En arrière plan, la noirceur de l'espace et l'horizon terrestre.
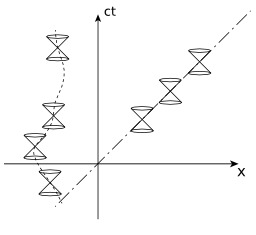
Deux lignes d'univers
Deux exemples de lignes d'univers : En physique, la ligne d'univers d'un objet est la trajectoire d'un objet lorsqu'il voyage à travers l'espace-temps en 4 dimensions. Le concept de ligne d'univers se distingue du concept de l'« orbite » ou de la « trajectoire » (tel que l'orbite d'un corps dans l'espace ou la trajectoire d'un camion sur une route) par la dimension temporelle. L'idée des lignes d'univers trouve son origine dans la physique et Einstein en fut le pionnier. Le terme est maintenant utilisé le plus souvent dans les théories de la relativité (générale ou restreinte, par exemple). Cependant, les lignes d'univers sont une manière de représenter le cours des événements. Son utilisation n'est pas liée à une théorie spécifique. Dans un usage général, une ligne d'univers est un chemin séquentiel d'événements (avec le temps et l'endroit comme dimensions) qui marquent l'histoire d'un objet. Le carnet de bord d'un navire est une description de sa ligne d'univers, pour autant qu'il comprenne une « étiquette de temps » attachée à chaque position. Il en va de même pour la vitesse d'un navire selon une mesure de distance (appelée métrique) appropriée à la courbe de la surface de la Terre.
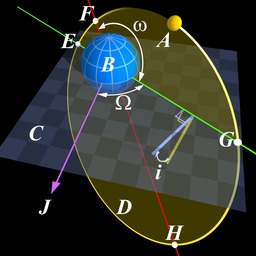
Les éléments orbitaux
Diagramme de Kepler des éléments orbitaux. F périapse, H apoapse, la ligne rouge entre eux est la ligne des apsides. Apsides, en astronomie, désigne les deux points extrêmes de l'orbite d'un objet céleste pour lesquels la distance est minimale (apside inférieure, ou périapside ou périapse) ou maximale (apside supérieure, ou apoapside, ou apoapse) par rapport au foyer de cette orbite. Le mot s'emploie plus rarement au singulier pour désigner l'un ou l'autre des deux points. La ligne qui relie le périapside et l'apoapside d'une orbite donnée est appelée ligne des apsides. C'est l'axe principal de l'ellipse, la ligne la plus longue qui joint les deux points les plus éloignés.
Modèle de l'orbite lunaire en 1557
Modèle de l'orbite lunaire de 1557 ayant appartenu à Vincenzo Viviani (1622-1703), disciple de Galilée ; Musée Galilée, Florence.
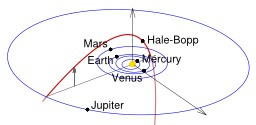
Orbite de la comète de Hale-Bopp
Orbite de la comète Hale-Bopp. La position de la comète et des planètes sont données au 1er avril 1997, le périhélie. Basé sur les données d'éphémérides de "horizons" par la NASA.
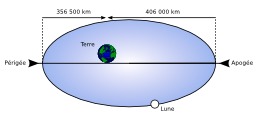
Orbite lunaire elliptique
Illustration du rythme anomalistique dû à l'orbite lunaire elliptique. L'orbite elliptique de la Lune détermine un passage à une distance minimale de la Terre (environ 360000 Km) ou périgée (Pg) et maximale nommée apogée (Ag) situé à environ 406000 Km de la Terre. Ce rythme dure environ 27,55 jours.
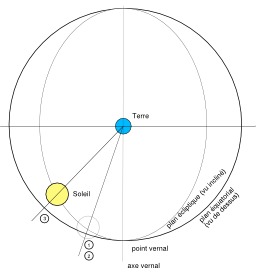
Orbite Terre-Soleil dans un référentiel géocentrique
Orbite Terre Soleil dans un référentiel géocentrique (c'est-à-dire la Terre étant fixe au centre de la figure et le Soleil orbitant autour de la Terre) : illustration des étapes nécessaires pour qu'un méridien terrestre donné retourne face au Soleil d'un jour au suivant. 1) une rotation complète (360°) de la Terre sur elle-même pour passer de 1 à 2 ; 2) ce faisant, le Soleil a avancé sur son orbite autour de la Terre, et de ce fait la Terre montre ce même méridien non pas face au Soleil mais face aux étoiles lointaines, point 2 ; 3) une rotation complémentaire de la Terre sur elle-même est alors nécessaire pour que le méridien soit à nouveau face au Soleil, point 3.