Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Cadran solaire de Carcassonne
Cadran solaire à Carcassonne (Aude, France). Conçu en 1961 par René R. J. Rohr (1905-2000). La table de conversion en bas à droite permet de l'utiliser comme cadran lunaire. Inscriptions en latin : CARPE DIEM = "Cueille le jour" (Horace, Odes) ; ANNO ¯DMI MCMLXI [Anno Domini MCMLXI] = L'an 1961 de Notre Seigneur ; HORAE / DIES = Heures / Jour ; RRJ ROHR FECIT = Fait par René R. J. Rohr. René Rodolphe Joseph Rohr était un spécialiste français en gnomonique. Il fut l’auteur de traités et d’articles de référence sur les cadrans solaires, leur conception et leur historique. Gnomoniste, il a également conçu ou restauré de nombreux cadrans solaires. Il est plus connu comme René R. J. Rohr (publications), René Rohr (en Alsace), ou R. R. J. Rohr (anglo-saxons).
Dessins et plans, Cube, Carré, Géométrie des nombres, Gnomonique, Abu Bakr Muhammad ibn al-Hasan al- Karaji (....-1019 ?)
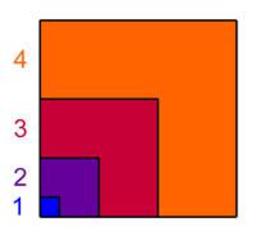
Carré d'un nombre triangulaire
Démonstration géométrique de la formule donnant le carré d'un nombre triangulaire, égal à la somme des premiers cubes parfaits : le carré du nième nombre triangulaire est égal à la somme des n premiers cubes. L'illustration géométrique permet de se convaincre de la véracité de ses propositions. L'aire de la zone orange de la figure est appelée nombre gnomonique. Elle est constituée de deux rectangles de base 4 et de côté le nombre triangulaire d'indice 4, c'est-à-dire 10. Ces deux rectangles se recoupent sur un carré de côté 4, on en déduit que l'aire orange est égale à 5 x 4 x 4 - 4 x 4, ou encore 43. Ce raisonnement est valable sur chaque nombre gnomonique, l'aire du carré de côté le nombre triangulaire d'indice 4 est égal la somme des 4 premiers cubes. De cette démonstration d'Al-Karaji, on déduit la première proposition.