Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Horloges et montres, Arithmétique, Aiguilles (horlogerie), Arithmétique modulaire, Heures
Arithmétique modulo avec les aiguilles de l'heure
L'aiguille des heures matérialise l'arithmétique modulo 12 ; l'« arithmétique de l'horloge » se réfère à l'« addition » des heures indiquées par la petite aiguille d'une horloge : concrètement, si nous commençons à 9 heures et ajoutons 4 heures, alors plutôt que de terminer à 13 heures (comme dans l'addition normale), nous sommes à 1 heure. De la même manière, si nous commençons à minuit et nous attendons 7 heures trois fois de suite, nous nous retrouvons à 9 heures (au lieu de 21).
Arithmetria.jpg
Scan par Nick Michael de Beham, (Hans) Sebald (1500-1550) : Arithmetria (B.124, P.126), extrait de "The Seven Liberal Arts", P., Holl. 123-129.
Arithmomètre de Charles Xavier Thomas vers 1820
Arithmomètre de Charles Xavier Thomas vers 1820 exposé au musée des techniques de Stockholm en Suèden.
Dessins et plans, Abaques (mathématiques), Arithmétique, Unités arithmétiques et logiques, Cinq (le nombre), Multiplication (arithmétique), Bouliers
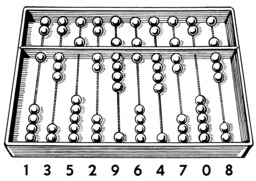
Boulier-Abaque
Croquis d'un abaque boulier : les unités sont placées en haut de la tige inférieure et les multiples de cinq en bas de la tige supérieure ; le nombre se lit donc au milieu du boulier ; chaque colonne peut représenter les nombres de 0 à 15 pour le report des retenues par multiples de 5. Voici le décompte de 1352964708, de gauche à droite : 1 = 1 + 0x5 ; 3 = 3 + 0x5 ; 5 = 0 + 1x5 ; 2 = 2 + 0x5 ; 9 = 4 + 1x5 ; 6 = 1 + 1x5 ; 4 = 4 + 0x5 ; 7 = 2 + 1x5 ; 0 = 0 + 0x5 ; 8 = 3 + 5x1.
Dessins et plans, Arithmétique, Nombre d'or, Spirales, Mathématiques, Suite de Fibonacci, Carrés magiques
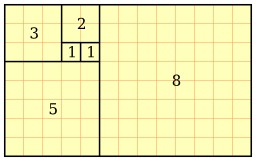
Carrés de Fibonacci en spirale
Une spirale logarithmique peut être approchée de la manière suivante : on commence à l'origine d'un repère cartésien, on se déplace de mathcal F_1 unités vers la droite, puis de mathcal F_2 unités vers le haut, on se déplace de mathcal F_3 unités vers la gauche, ensuite de mathcal F_4 unités vers le bas, puis de mathcal F_5 unités vers la droite, etc. Cela ressemble à la construction mentionnée pour le nombre d'or.
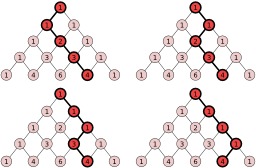
Chemins binaires dans le triangle de Pascal
Les quatre chemins binaires dans le triangle de Pascal : Imaginons que chaque nombre dans le triangle est un nœud dans un réseau qui est connecté aux nombres adjacents du dessus et du dessous. Maintenant pour n'importe quel nœud dans le réseau, comptons le nombre de chemins qu'il y a dans le réseau (sans faire marche arrière) qui connecte ce nœud au nœud supérieur du triangle. La réponse est le nombre de Pascal associé à ce nœud.
Photographie, Couleurs, Arithmétique, Jeux mathématiques, Matériel didactique, Quatre (le nombre), Dix-huit (le nombre), Dix (le nombre), Georges Cuisenaire (1891-1975), Méthodes d'apprentissage
Construire dix avec les réglettes cuisenaire
Construire dix avec dix-huit réglettes cuisenaire de quatre couleurs différentes
Dessins et plans, Calcul, Horloges et montres, Arithmétique, Aiguilles (horlogerie), Arithmétique modulaire
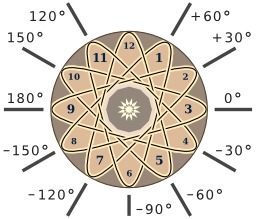
Correspondances heures et angles
Douze angles définis modulo 360 degrés correspondent à des temps, définis modulo 12 heures. Par exemple, une aiguille d’horloge a une seule position numérotée zéro ou vingt-quatre, parce que 0 = 24 modulo 12. Cette position correspond à 90 ou –270 degrés modulo 360 degrés. Ainsi nous identifions direction et sens d’une demi-droite ou d’un vecteur en coordonnées polaires, ou l’angle d’une rotation donnée, ou l’argument d’un nombre complexe donné. Le dessin sur le cadran de l’horloge évoque des progressions arithmétiques de raisons 5 ou 7 modulo 12. Par exemple, en tournant dans le sens des aiguilles d’une montre à partir de 1, nous passons par les termes : 1, 6, 11, 4, 9, 2, 7, 12, 5, 10, 3, 8. Cette suite correspond à une progression de raison arithmétique 210 degrés modulo 360 degrés. Si les douze positions d’une aiguille d’horloge sont numérotées dans l’ensemble P de douze éléments, de 1 à 12 modulo 12, et si l’ensemble A est constitué des angles indiqués dans l’image, une bijection B de P sur A peut être définie par B( t ) = 90 – 30 t. Par exemple, B( 12 ) = 90 – 30 × 12 = 90 degrés modulo 360 degrés. L'arithmétique modulaire est un système arithmétique d'entiers modifiés, où les nombres sont « abaissés » lorsqu'ils atteignent une certaine valeur. Donnons comme exemple, l'« arithmétique de l'horloge » qui se réfère à l'« addition » des heures indiquées par la petite aiguille d'une horloge : concrètement, si nous commençons à 9 heures et ajoutons 4 heures, alors plutôt que de terminer à 13 heures (comme dans l'addition normale), nous sommes à 1 heure. De la même manière, si nous commençons à minuit et nous attendons 7 heures trois fois de suite, nous nous retrouvons à 9 heures (au lieu de 21). Fondamentalement, quand nous atteignons 12, nous recommençons à zéro ; nous travaillons modulo 12. Pour reprendre l'exemple précédent, on dit que 9 et 21 sont congrus modulo 12. Les nombres 9 ; 21 ; 33 ; 45 ; etc. sont considérés comme égaux lorsqu'on travaille modulo 12. Pour généraliser, nous pouvons facilement imaginer une horloge qui contient un nombre arbitraire d'heures, et faire des calculs avec un nouveau modulo.
Photographie, Arithmétique, Cahiers d'écolier, Anglais (langue), Concord (Mass.), Division numérique
Division à l'anglaise
Cahier de classe en arithmétique, la division, 1815-1835. Exposition au Concord Museum, Concord, Massachusetts, USA.
Photographie, Doigts, Arithmétique, Jeux de doigts, Contribution à la pédagogie, Bède le Vénérable (saint, 0673?-0735), Jacob Leupold (1674–1727), Livres à compter
L'art de compter avec les doigts en 1727
L'art de compter avec les doigts en 1727, "Theatrum arithmetico geometricum" par Jacob Leupold (1674–1727), à partir de la méthode pédagogique de Bede le Vénérable, mort en 735.
Dessins et plans, Arithmétique, Treizième siècle, Blaise Pascal (1623-1662), Mathématiques, Lapins, Triangle de Pascal, Populations d'animaux, Suite de Fibonacci
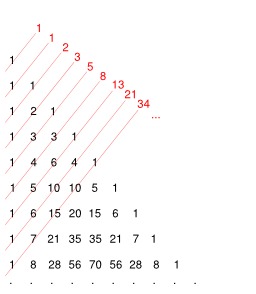
La suite de Fibonacci
Triangle de Pascal et suite de Fibonacci : La somme des diagonales ascendantes du triangle de Pascal forme la suite de Fibonacci. Leonardo Fibonacci (v. 1175-1250). Elle doit son nom à Leonardo Fibonacci, dit Leonardo Pisano, un mathématicien italien du XIIIe siècle qui, dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci, décrit la croissance d'une population de lapins : « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? » Cette suite est fortement liée au nombre d'or, φ (phi). Ce nombre intervient dans l'expression du terme général de la suite. Inversement, la suite de Fibonacci intervient dans l'écriture des réduites de l'expression de φ (phi) en fraction continue : les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or.
Dessins et plans, Arithmétique, Mathématiques, Lapins, Populations d'animaux, Leonardo Fibonacci (v. 1175-1250)
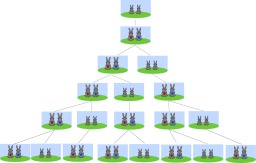
Les lapins de Fibonacci
Croissance de population des lapins selon une suite de Fibonacci (Leonardo Fibonacci, v. 1175-1250). « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? »
Nombre triangulaire
Le 28 est le septième nombre triangulaire ou encore le nombre triangulaire d'indice 7 : en arithmétique, un nombre triangulaire est un cas particulier de nombre figuré. Il correspond à un nombre entier positif égal au nombre de pastilles dans un triangle construit à la manière de cette figure. Source : p. 320, Die Gartenlaube (1887), Ernst Keil's Nachfolger.
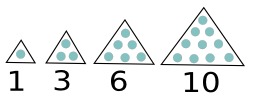
Nombres triangulaires
Représentation graphique des premiers nombres triangulaires : la représentation figurée permet un calcul pour les premières valeurs. Une définition formelle s'obtient par récurrence : le nombre triangulaire d'indice 1 est égal à 1, et un nombre triangulaire est égal à son prédécesseur additionné de son indice. Les premiers nombres triangulaires sont : 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ... Il existe différentes manières de calculer le nombre triangulaire d'indice n, l'une d'elles est graphique et s'obtient par un raisonnement d'arithmétique géométrique.
Clip art, Arithmétique, Multiplication (arithmétique), Signes et symboles, Addition, Soustraction, Fractions, Opérations (arithmétique), Sciences -- Notation
Quatre symboles arithmétiques
Quatre symboles d'opérations arithmétiques : addition (jaune), fraction (vert), soustraction (bleu) et multiplication (violet).
Photographie, Couleurs, Arithmétique, Jeux mathématiques, Matériel didactique, Dix (le nombre), Vingt (le nombre), Georges Cuisenaire (1891-1975), Méthodes d'apprentissage
Vingt réglettes cuisenaire
Vingt réglettes cuisenaire de dix couleurs différentes. Georges Cuisenaire (1891-1975) était un pédagogue belge qui inventa la méthode des réglettes couleur pour l'apprentissage de l'arithmétique, auteur de "Les nombres en couleur".