Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Fourmis, Animaux -- Comportement alimentaire, Insectes, Biologie animale, Algorithmes, Optimisation par colonies de fourmis, Algorithmes bio-inspirés (intelligence artificielle), Animaux -- Moeurs et comportement -- Mesure
Algorithme des fourmis
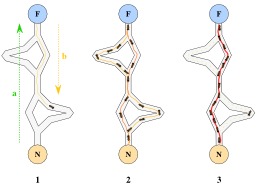
Choix du plus court chemin par une colonie de fourmis : 1) la première fourmi trouve la source de nourriture (F), via un chemin quelconque (a), puis revient au nid (N) en laissant derrière elle une piste de phéromone (b) ; 2) les fourmis empruntent indifféremment les 4 chemins possibles, mais le renforcement de la piste rend plus attractif le chemin le plus court ; 3) les fourmis empruntent le chemin le plus court, les portions longues des autres chemins voient la piste de phéromones s'évaporer. Source : Commentaire de l'auteur.
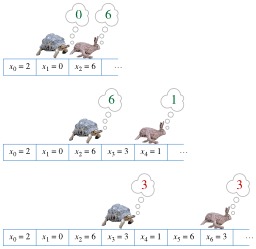
Algorithme du lièvre et de la tortue
Algorithme de Floyd, algorithme de détection de cycle. Le lièvre et la tortue, fable d'Ésope (0620?-0560? av. J.-C.).
Dessins et plans, Géométrie, Triangle, Mathématiciens, Itération (mathématiques), Algorithmes, Savants polonais, Wacław Sierpinski (1882-1969), Fractales, Récursivité, Théorie de la
Évolution du triangle de Sierpinski
Évolution du triangle de Wacław Sierpinski (1882-1969) en 5 itérations. Un algorithme pour obtenir des approximations arbitrairement proches du triangle de Sierpiński peut s'écrire de la manière suivante : 1-Commencer à partir d'un triangle quelconque du plan. Le triangle canonique de Sierpiński se construit à partir d'un triangle équilatéral ayant une base parallèle à l'axe des abscisses ; 2-Tracer les trois segments qui joignent deux à deux les milieux des côtés du triangle, ce qui délimite 4 nouveaux triangles ; 3-Enlever le petit triangle central. Il y a maintenant trois petits triangles qui se touchent deux à deux par un sommet, dont les longueurs des côtés sont la moitié de celles du triangle de départ (obtenue par une homothétie de rapport 1/2), et dont l'aire est divisée par 4. 4-Recommencer à la deuxième étape avec chacun des petits triangles obtenus.
Peinture, Peinture de portraits, Dix-neuvième siècle, Aquarelles, Inventeurs, Portraitistes, Algorithmes, Mathématiciennes, Ada King Lovelace (comtesse de, 1815-1852), Programmeurs, Savants britanniques
Portrait de Ada Lovelace en 1840
Portrait par Alfred Edward Chalon (1780-1860) de Ada King Lovelace (comtesse de, 1815-1852) en 1840, mathématicienne, fille de Lord Byron, épouse de William King, comte de Lovelace ; première programmatrice inventrice de l'algorithme en 1843. Source : http://fr.wikipedia.org/wiki/Ada_Lovelace