Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Kairouan (Tunisie) -- Grande mosquée, Symétrie, Symétrie (art), Arcades, Architecture islamique
Arcades symétriques de la mosquée de Kairouan
Vue intérieure des arcades symétriques du portique situé du côté occidental de la cour de la Grande Mosquée de Kairouan, en Tunisie.
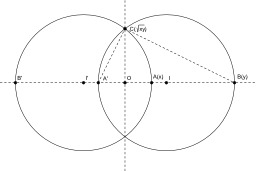
Calcul de racine carrée au compas
Construction au compas seul de la racine carrée du produit xy. Si A a pour abscisse x et B pour abscisse y, on construit les points A' et B' d'abscisses -x et -y Les cercles de diamètres [AB'] et [A'B] se coupent sur l'axe des ordonnées en un point d'ordonnée sqrt{xy} (propriété de la hauteur dans un triangle rectangle). Il est toujours possible de rabattre sqrt{xy} en abscisse par symétrie par rapport à la première bissectrice (constructible au compas).
Dessins et plans, Géométrie, Tapis, Architecture -- Dessins et plans, Symétrie, Tapis persans, Art iranien, Systèmes de quadrillage, Art décoratifs, Tapis -- Cartons
Carton de tapis iranien
Angle d'un plan ("carton") de tapis iranien à formes géométriques, avec indication des couleurs, sur papier quadrillé.
Photographie, Géométrie, Tapis, Croquis (art), Symétrie, Arts décoratifs, Tapis persans, Art iranien, Tapis -- Modèles, Tapis -- Cartons
Cartons de tapis iraniens
Plans ("cartons") de tapis iraniens sur papier quadrillé avec indications de coloriage.
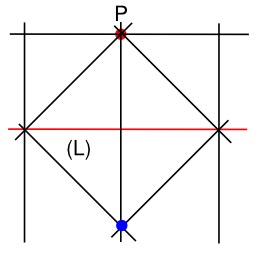
Construction d'un point symétrique par pliage
Construction du symétrique d'un point par rapport à une droite par origami : On construit la perpendiculaire à (L) passant par P puis la perpendiculaire à cette perpendiculaire passant par P (autrement dit, la parallèle à (L) passant par P). On construit les deux bissectrices en P à la parallèle à (L) et la perpendiculaire à (L). Ces deux bissectrices vont couper (L) en deux points d'où l'on trace deux nouvelles perpendiculaires à (L). Deux dernières bissectrices vont se couper en le symétrique à P cherché.
Dessins et plans, Géométrie, Compas, Règles, Parallèles (géométrie), Symétrie, Constructions géométriques
Construction d'une parallèle
Construction à la règle et au compas d'une parallèle à une droite passant par un point donné : La parallèle à la droite (AB) passant par un point C se construit à l'aide de la propriété de la droite des milieux. On construit le symétrique C1 du point C par rapport à A puis le symétrique C2 du point C1 par rapport à B. la droite recherchée est la droite (CC2). Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès.
Peinture, Cygnes, Art nouveau, Dix-neuvième siècle, Peintres anglais, Symétrie, Art nouveau (décoration), Décoration et ornement -- Art nouveau, Symétrie (art)
Deux cygnes
Deux cygnes, décor de papier peint, 1875, par Walter Crane (1845-1915), peintre anglais du mouvement de l'Art Nouveau.
Photographie, Symétrie, Symétrie (art), Frises, Architecture romaine, Translation (physique), Mouvement de
Frise décorative en architecture
Frise décorative imitant l'antique, 138-146 West 14° Rue, entre la 6° et la 7° Avenues à Manhattan, New York City datant de 1899. Les frises décoratives en architecture sont souvent des structures symétriques par translation : si on déplace la structure de la largeur d'un motif, on retrouve la même structure.
Dessins et plans, Géométrie, Solides, Tétraèdres, Polyèdres, Groupes de rotations, Symétrie, Symétrie (physique)
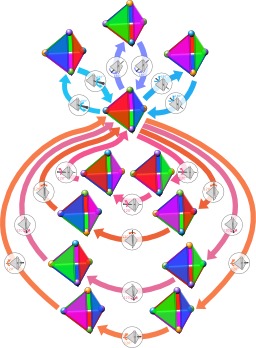
Groupe de symétrie du tétraèdre régulier
Un tétraèdre régulier peut être placé dans 12 positions distinctes par une seule rotation. Celles-ci sont illustrées dans le format d'un graphe de cycles avec des rotations à 180° par rapport à une arête (flèches bleues) et à 120° par rapport à un sommet (flèches rouges) qui permutent le tétraèdre dans toutes les positions. Les 12 rotations forment le groupe (de symétrie) de rotation de la figure.
La lapine devant son miroir du terrier d'Abulédu
La lapine devant son miroir du terrier d'Abulédu, par E. François et F. Audirac, 20080101.
Le lapin et son double du terrier d'Abulédu
Le lapin et son double du terrier d'Abulédu, par E. François et F. Audirac, 20080101.
Rotations du tétraèdre
Rotations du tétraèdre : Tout groupe de symétrie dont les éléments ont un point fixe commun, ce qui est vrai pour tous les groupes de symétrie de figures bornées, peut être représenté comme un sous-groupe du groupe orthogonal O(n) en choisissant comme origine un point fixe. Le groupe de symétrie propre est alors un sous-groupe du groupe spécial orthogonal SO(n), c'est pourquoi il est aussi appelé le groupe de rotation de la figure.
Photographie, Dessins et plans, loup, Lièvres, Bateaux, Grenouilles, Antiquités, Gravure, Peinture, Clip art, Balles et ballons, Amphibiens, Fleurs, Géométrie, Couleurs, Accumulateurs, Piles électriques, Plages, Forêts, Sable, Parasols, Cuisine (pain), Jardinage, Jardins, Réfrigérateurs, Réfrigération et appareils frigorifiques, Bains, Bovins de boucherie, Crustacés, Cuisine -- Appareils et matériel, Nuages, Produits viticoles, feu, Linux (système d'exploitation des ordinateurs), Compas, Salades, Livres illustrés pour enfants, Ombres, laine, Poisson, Plantes des jardins, Confitures, Outillage, Pêches, Cartes à jouer, Mer, Architecture végétale des jardins, Légumes, Potages, Navires à voiles, Découpage (cuisine), Viande, Viande -- Coupe, Étoiles, Cuisine (porc), Saucisses, Enseignes, Tables (meubles), Ongle, Cuisine (aliments naturels), Thé, Bleu, Mouton (viande), soleil, Cuisine (oeufs), Peur chez les animaux, Caricatures et dessins humoristiques, noir, Mécanique, Navires, Triangle, Oeufs, Baies (fruits), Porc, Émotions, Albums à colorier, Nombres cardinaux, Éléments de cuisine, Ustensiles de cuisine, Dinde (viande), Nouvelle-Zélande -- Civilisation, Boissons non alcoolisées, Peur, Pâtisseries, Familles, Fêtes -- Accessoires, Cuisine (fromage), Gelées (confiserie), Maillots de bain, Alimentation, Ciel, Temps -- Systèmes et normes, Oeufs -- Coquilles, Poissons d'eau douce, Parents et enfants, Cuisine (poisson), Véhicules prioritaires, Poulet (viande), Râteaux, Animaux des forêts, Cheminées, Couple -- Psychologie, Espace-temps, Cuisine (sucre), Bains de soleil, Terre, Veaux, Vents, Pyramides, Couple, Graines, Filage à la main, Poissons de mer, Rouge, Aluminium, Vert, Sacs, Membres, Cercle, Navires -- Équipement, Physique, Lumière, Lumière -- Propagation, Joie, Géologie -- Cartes, Poisson rouge, Saumon rouge, Agriculture -- Outillage, Coeur, Art médiéval, Trèfles, Pyramides -- Égypte, Cristaux, Blé, Batteries, Marbre, Fillettes, Caricature, Calcaire, Plantes méditerranéennes, Géométrie euclidienne, Navigation à voile, Cuisine (légumes verts), Sacs en tissu, Pelles, Thalès, Théorème de, Seizième siècle, Dix-neuvième siècle, Dix-septième siècle, Cuivre, Grumes, Albums, Pères, Pères et filles, Sentiers, Maisons individuelles, Pattes, Refus d'obéissance, Jardins médiévaux, Lièvre d'Europe, Méditerranée (région), Cuisine (thym), Aliments crus, Parapente, Vol libre, Dix-huitième siècle, France (Révolution) (1789-1799), Albrecht Dürer (1471-1528), Vinaigre, Poisson fumé, Poisson salé, Auckland (Nouvelle-Zélande), Nouvelle-Zélande (1945-....), Aliments, Cuisine (fruits), Aliments d'origine animale, Aliments fermentés, Cuisine (légumes), Produits de l'oeuf, Boissons alcoolisées, Hérodote (0484?-0420? av. J.-C.), Circulation, Vents -- Vitesse, Métamorphisme (géologie), Savants français, Cuisine (aliments crus), Cuisine (fruits de mer), Cuisine (aliments surgelés), Volaille (viande), Cuisine (poulet), Cuisine (volaille), Produits du blé, Sirops, Sauce à salade, Cuisine (viande), Cuisine (plantes odoriférantes), Crèmes (desserts), Entremets, Poisson surgelé, Agneau (viande), Desserts, Hors-d'oeuvre, Cuisine (baies), Cuisine (vinaigre), Ondes, Cuisine (céréales), Jeux de plage, Conduits d'évacuation de fumées, Fumées, Pull-over, Bronzage, Astérides, Seaux, Serviettes, Chlorure de sodium, Cycle hercynien, Boeuf (viande), Rôtis, Rotissoires, Plats complets, Astacidés, Cuisine (écrevisses), Décapodes (crustacés), Écrevisses, Vinaigrette, Champignons cultivés, Cuisine (champignons), Cuisine (truffes), Truffe du Périgord, Tubéracées, Cassis, Cassissier, Cuisine (cassis), Aliments -- Composition, Blanquette, Cuisine (veau), Veau (viande), Veaux -- Alimentation, Omble de fontaine, Poissonneries, Saumons, Saumons -- Pêche commerciale, Cuisine (semoule), Semoule, Cônes de pin, Pignons (graines), Aliments enrichis, Cuisine (restes), Tourtes, Deux, Jeux de société, Trois, Soupes, Infusions, Lumière, Théorie ondulatoire de la, Cuisson sur réchaud de table, Fondues, Savants allemands, Jumeaux, Interférence (optique), Rhubarbe, Augustin Fresnel (1788 - 1827), Diffraction, Ondes -- Diffraction, Énergie, Photons, Temps, Mesure du, France (Chute des Girondins) ( 30 mai-2 juin 1793), Exécutions capitales et exécuteurs, France (1793), Espace de Minkowski, Relativité (physique), Cônes de lumière, Relativité générale (physique), Architecture égyptienne, Constructions en pierres sèches, Cuisine (rhubarbe), Rhubarbes, Cuisine (boeuf), Cuisines, Aliments -- Consommation, Césium, Horloges à césium, Horloges atomiques, Berne (Suisse), Échelles de temps atomique, Temps (droit international), Johannes Kepler (1571-1630), Des révolutions des orbes célestes - Nicolas Copernic (1473-1543), Héliocentrisme, Énergie éolienne en mer, Portance, Aérodynamique, Relativité restreinte (physique), Muons, Rayons cosmiques, Aquarelle, Le lièvre - Albrecht Dürer (1471-1528), Peintres allemands, Cuisine (plantes aromatiques), Résistance à la chaleur, Thymus (plantes), Abats, Cuisine (abats), Tripes, Aliments -- Réfrigération, Entreposage frigorifique, Frigidaire, Frigo, Danse maorie, Ethnologie -- Nouvelle-Zélande, Linux (logiciels), Rugby, Bayonne (Pyrénées-Atlantiques), Ferias, Aliment, Chevreau (viande), Tacuini sanitatis - al-Muẖtār ibn al-Ḥasan ibn ʿAbdūn ibn Saʿdūn Ibn Buṭlān (10..-1066?), Tangram, Corrosion, Corrosion électrochimique, Assemblages à rivets, Corrosion galvanique, Réactions chimiques -- Mécanismes, Électricité, Symétrie, Constructions géométriques, Génie mécanique, Ressorts et suspension, Ressorts, Volutes, Algues marines, Algues -- Aspect économique, Navires -- Australie, Navires -- Déchets -- Élimination, Navires océanographiques, Navires -- Règlements de sécurité, Sargasses, Mer des, Auteurs arabes, Yuwānīs Ibn Buṭlān (10..-1066?), Jardins -- Aspect symbolique, Famille -- Anthropologie, Famille -- Loisirs, Famille -- Santé et hygiène, Mouton (laine), Quenouilles, Regroupement familial, Veillées, Scènes de la vie quotidienne, Vie quotidienne, Révolution industrielle, Projection cinématographique, Signes et symboles, Carreau, Cartes à jouer, Jeux avec, Pique, Trèfle, Chaleur -- Convection, Dissipateurs thermiques (électronique), Électronique, Acides aminés, Protéines
Dessins et plans, Neige, Dix-septième siècle, Savants français, Savants allemands, Johannes Kepler (1571-1630), Hexagones, Symétrie, Symétrie (physique), Cristallographie, Cristaux de neige, Astronomes, René Descartes (1596-1650)
Schémas de cristaux de neige par Descartes
Schémas de cristaux de neige par René Descartes (1596-1650), à partir de l'ouvrage de Johannes Kepler (1571-1630). En 1611, Kepler publie "L’Étrenne ou la neige sexangulaire", premier traité scientifique de 24 pages qui étudie les cristaux de neige, observant notamment leur symétrie hexagonale. René Descartes observe en 1635 à l'œil nu des cristaux de neige et décrit notamment des formes rares, cristaux à douze branches, plaques hexagonales et colonnes.
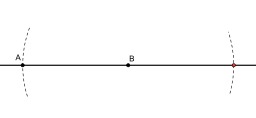
Symétrique d'un point par rapport à un point
Construction du symétrique d'un point A par rapport à un point B, à la règle et au compas.
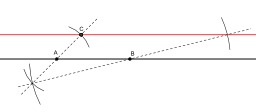
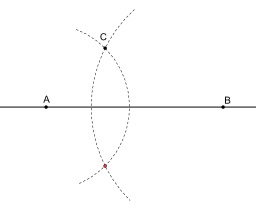
Symétrique d'un point par rapport à une droite
Construction du symétrique d'un point C par rapport à une droite à la règle et au compas : Le symétrique du point C par rapport à la droite (AB) s'obtient en construisant le point d'intersection (différent de C) entre le cercle de centre A passant par C et le cercle de centre B et passant par C. Si le point C est sur la droite (AB), il est son propre symétrique et aucune construction n'est nécessaire.
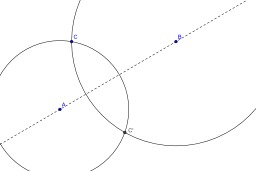
Symétrique d'un point par rapport à une droite
Construction au compas seul du symétrique d'un point par rapport à une droite. Le symétrique du point C par rapport à la droite (AB) est le point d'intersection des cercles de centres A et B et passant par C. Dans la construction la droite (AB) est tracée en pointillés pour permettre de suivre le raisonnement mais elle ne sert pas en tant que telle dans la construction. En géométrie classique plane, le théorème de Mohr Mascheroni, démontré par Georg Mohr en 1672 et par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas seul (sauf le tracé effectif des droites). Est considéré comme constructible tout point d'intersection de deux cercles dont les centres sont des points déjà construits et dont les rayons sont des distances entre des points déjà construits.