Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Dessins et plans, Géométrie, Carré, rectangle, rectangles, Angles, Parallèles (géométrie), Parallélogrammes, Polygones, Tablettes d'argile cunéiformes, Pentagones, Diagonales, Racine carrée de deux, Losanges, Quadrilatères, Trapèzes, Aires (surfaces), Aires (surfaces) -- Mesure
Parallélograme
Exemple de parallélogramme. Un parallélogramme, en géométrie, est un quadrilatère dont les côtés opposés sont parallèles deux à deux
Photographie, Géométrie, Carré, Triangle, Urbanisme, Isostasie, Égouts, Plaques de regard, Structures hyperstatiques
Plaque d'égout isostatique
Plaque d'égout isostatique : une plaque d'égout classique n'est jamais parfaitement plane ni l'appui sur lequel elle repose. Il en résulte un bruit de basculement, métal sur métal, chaque fois qu'on marche dessus ou, plus énervant encore, lorsqu'une roue de voiture la traverse. La solution a consisté à supprimer cet appui hyperstatique et à le remplacer par un appui en trois points : deux demi-plaques triangulaires jumelles dessinent un carré coupé en diagonale. Ces demi-plaques sont articulées selon deux côtés opposés du carré, le troisième appui étant constitué par la pointe que l'on relève pour accéder au regard. Source : http://fr.wikipedia.org/wiki/Plaque_d%27%C3%A9gout
Somme de huit nombres triangulaires
La somme de huit fois un nombre triangulaire et de un est un carré parfait.
Dessins et plans, Carré, Surfaces (mathématiques) -- Volumes, Géométrie des nombres, Johann Faulhaber (1580-1635), Pyramides (géométrie)
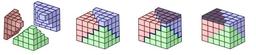
Somme des carrés
Un exemple de preuve sans mots à propos de la somme des premiers carrés : chacune des trois pyramides a pour volume la somme des carrés de 1 à n (n=4 dans cette illustration) ; le parallélépipède final est de côtés n, n+1 et n+1/2. Ce résultat se généralise pour la somme des n premières puissances strictement positives. Cette somme porte le nom de formule de Faulhaber. Johann Faulhaber (1580-1635) est un mathématicien allemand qui collabora avec Kepler.
Dessins et plans, Géométrie, Carré, Jeux mathématiques, Origami, Pliages en papier, Théorèmes -- Démonstration automatique, Mathématiques japonaises, Nombres rationnels
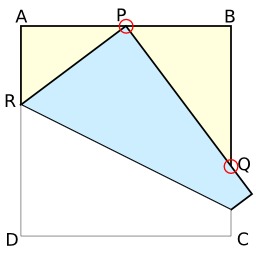
Théorème de Haga et origami
Théorème de Haga et origami : BQ est rationnel si AP l'est, par pliage du sommet d'un carré sur un point P du côté opposé. Source : http://en.wikipedia.org/wiki/Mathematics_of_origami.