Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Géométrie, hiver, Branches, Rosée, Art et photographie, Toiles d'araignée, Point de rosée
Toile d'araignée entre deux branches dans la rosée
Toile d'araignée dans la rosée du matin après un brouillard d'hiver. Elle est constituée d'un cadre porteur en général vertical, de rayons et enfin d'une spirale en soie collante qui seule peut retenir les proies qui viennent heurter la toile en volant. Source : http://fr.wikipedia.org/wiki/Toile_d%27araign%C3%A9e
Photographie, Géométrie, Architecture médiévale, Terre vernissée, La Rochepot (Côte-d'Or) -- Château
Toiture en tuiles vernissées du Chateau La Rochepot
Toiture en tuiles vernissées du Chateau La Rochepot en Bourgogne.
Dessins et plans, Géométrie, Crayons, Règles, Dessin -- Matériel, Dessin industriel, Dessin -- Instruments, Dessin -- Technique, Lignes du quadrillage, Dessin à l'encre
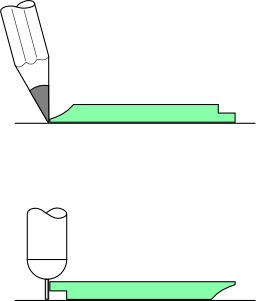
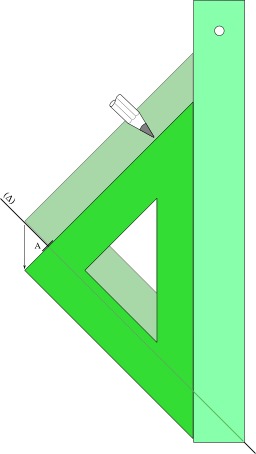
Tracé au crayon et à l'encre
Pour un tracé précis, il faut prendre en compte l'épaisseur de la mine de crayon ; on fait d'abord un tracé avec un crayon bien taillé, ou un critérium à mine fine, et à mine dure (qualité H, 2H, 3H, 4H) en appuyant légèrement ; puis, on repasse le résultat final à l'encre (stylo à bille ou à encre liquide) en laissant les traits de construction (on ne gomme pas) ; les outils de traçage — règles et équerres — présentent une « marche » sur certains côtés : si l'on fait un tracé au crayon ou au stylo bille, on utilise l'outil « à l'endroit », les graduations sont lisibles, le crayon ou le stylo est en contact avec le papier et avec l'outil ; si l'on fait un tracé à l'encre, par exemple avec un stylo à plume ou à mine tubulaire, on retourne l'outil, ainsi la pointe n'est pas en contact avec l'outil et l'encre ne risque pas de baver lorsque l'on enlève l'outil : Les règles et équerres on une marche qui permettent de dessiner à l'encre sans laisser de traînées lorsque l'on bouge les outils.
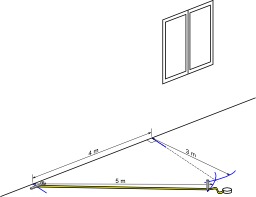
Trace d'une perpendiculaire avec la méthode du 3 4 5
Tracé d'une perpendiculaire en maçonnerie, méthode du 3-4-5 : le triangle est rectangle (théorème de Pythagore).
Dessins et plans, Géométrie, Règles, Dessin -- Matériel, Dessin -- Instruments, Ligne (art), Dessin -- Technique, Lignes du quadrillage, Points (mathématiques), Ensembles de
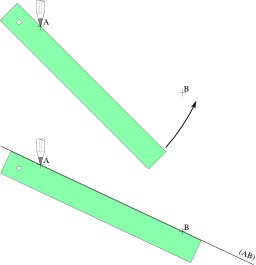
Tracer une droite entre deux points avec une règle
Comment prendre en compte la largeur de la mine pour tracer un trait entre deux points : 1) placer le crayon sur un des points A ; s'en servir comme pivot pour la règle vers le point B. 2) tracer un trait passant par ces deux point avec la règle.
Dessins et plans, Géométrie, Règles, Dessin -- Matériel, Parallèles (géométrie), Dessin -- Instruments, Dessin -- Technique, Lignes du quadrillage
Tracer une parallèle avec une règle et une équerre
Métode pour tracer une parallèle avec une règle et une équerre. On prend une équerre et l'on appuie un côté sur la droite de référence. On place une règle contre un autre côté de l'équerre. Puis, on appuie fermement sur la règle, et l'on fait glisser l'équerre contre la règle sans appuyer sur l'équerre, ceci afin d'éviter de faire bouger la règle. Source : Mécanique pour l'enseignement technique industriel/Éléments de géométrie (fr.wikiversity.org ).
Dessins et plans, Géométrie, Règles, Dessin -- Matériel, Dessin -- Instruments, Dessin -- Technique, Lignes du quadrillage
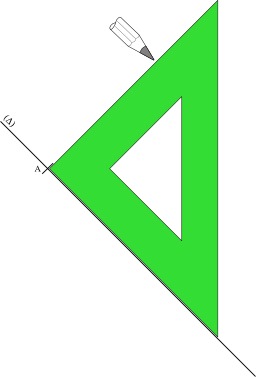
Tracer une perpendiculaire à une droite en un point avec une équerre
Méthode pour tracer une perpendiculaire à une droite en un point avec une équerre : on place un côté de l'angle droit de l'équerre contre la droite, l'angle droit étant contre le point considéré. Puis, on trace la ligne contre l'autre côté de l'angle droit. Cette méthode est simple, mais l'angle droit de l'équerre est en général émoussé, il est donc difficile d'être précisément sur le point.
Tracer une perpendiculaire précise
Méthode précise pour tracer une perpendiculaire en un point à une droite : placer un côté de l'angle droit de l'équerre contre la droite, un peu à côté du point ; placer une règle contre l’hypoténuse de l'équerre ; faire glisser l'équerre contre la règle jusqu'à ce que le point soit sur l'autre côté de l'angle droit, à l'épaisseur du crayon près. Pour cela, on appuie fermement sur la règle — elle est le guide et doit donc rester en place —, mais on reste très léger sur l'équerre ; tracer la ligne.
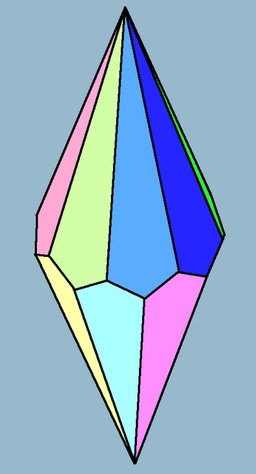
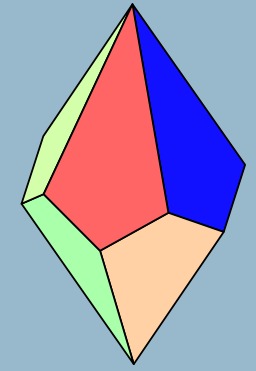
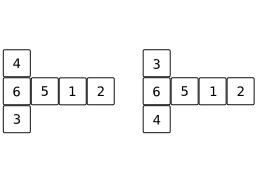
Trapézoèdre hexagonal
Trapézoèdre hexagonal. La partie n-gonale du nom ne fait pas référence aux faces mais à l'arrangement des sommets autour d'un axe de symétrie. L'antiprisme dual n-gonal possède deux faces n-gonales. Un trapézoèdre n-gonal peut être décomposé en deux pyramides n-gonales égales et un antiprisme n-gonal.
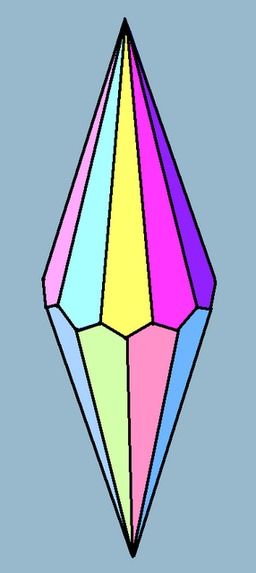
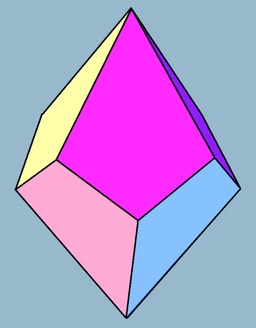
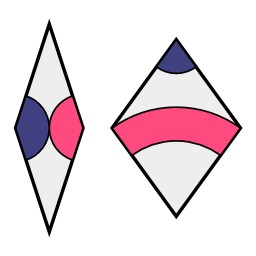
Trapézoèdre pentagonal
Trapézoèdre pentagonal : 10 faces en cerf-volant - dual : antiprisme pentagonal. Le trapézoèdre pentagonal est le premier solide différent des solides de Platon utilisé comme un dé dans les jeux de rôle tels que Donjons et Dragons. Ayant 10 côtés, il peut être utilisé en répétition pour générer n'importe quelle probabilité discrète désirée de base décimale.
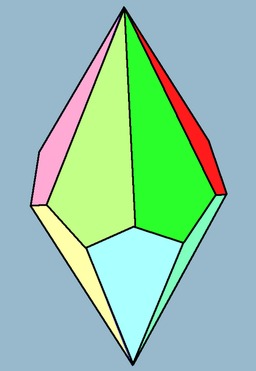
Trapézoèdre tétragonal
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces, par exemple le trapézoèdre tétragonal. Le nom trapézoèdre est trompeur puisque les faces ne sont pas des trapèzes. Le trapézoèdre ou antidiamant ou deltoèdre n-gonal est le polyèdre dual d'un antiprisme n-gonal régulier. Ses 2n faces sont des deltoïdes congrus (ou cerfs-volants). Les faces sont décalées symétriquement.
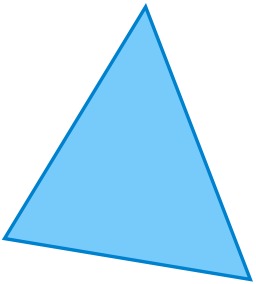
Triangle
Un triangle scalène : un triangle qui n'est ni isocèle (ce qui exclut également le cas équilatéral) ni plat est dit scalène (du grec σκαληνός (skalenos) : boiteux, inégal, déséquilibré, oblique...) Il s'agit donc d'un triangle ayant trois côtés de longueurs différentes, trois angles de mesures différentes et aucun axe de symétrie.
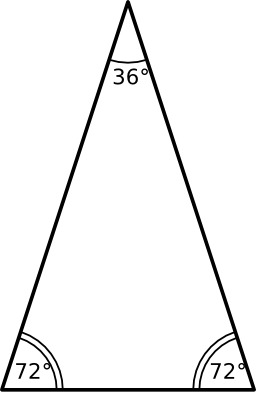
Triangle d'or
Le triangle d'or est un triangle isocèle dont les angles à la base valent deux cinquièmes de l'angle plat, soit 72° ;
Triangle de Sierpinski avec 7 itérations
Le triangle de Sierpiński, aussi appelé par Mandelbrot le joint de culasse de Sierpiński (1882-1969), est une fractale, du nom de Wacław Sierpiński. Il peut s'obtenir à partir d'un triangle « plein » par une infinité d'itérations consistant à diviser par deux la taille du triangle puis à en juxtaposer trois exemplaires par leurs sommets pour former un nouveau triangle. À chaque itération le triangle est donc de même taille, mais « de moins en moins plein ».
Triangle demi carre
Le demi-carré est un triangle isocèle rectangle, qui peut s'obtenir en reliant trois sommets d'un carré.
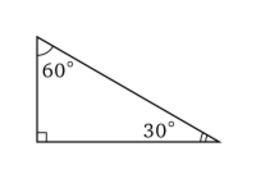
Triangle ecolier
Le triangle de l'écolier ou triangle hémi-équilatéral est un triangle rectangle dont les mesures des angles sont de 30°, 60° et 90° .
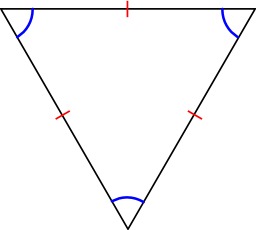
Triangle equilateral
Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur. Ses trois angles ont alors la même mesure qui vaut donc 60° et il admet trois axes de symétrie.
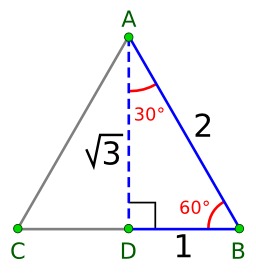
Triangle équilatéral
Représentation géométrique de fonctions trigonométriques : triangle équilatéral divisé en 2 pour calcul du sin, du cos, et de la tan pour 30° et 60°.
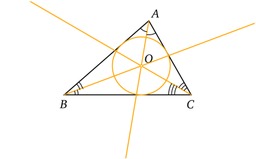
Triangle et bissectrices
Si le triangle est non plat, les trois bissectrices de ses angles (les demi-droites qui partagent les angles en deux angles de même mesure) sont concourantes en un point appelé centre du cercle inscrit, car il est le centre du seul cercle tangent aux trois côtés. Ce centre est en général noté I ou J.
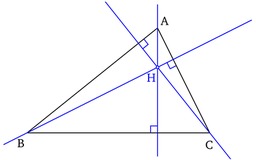
Triangle et hauteurs
Si les trois sommets sont distincts, une hauteur est une droite passant par un sommet et perpendiculaire au côté opposé. Si le triangle est non plat, les trois hauteurs sont concourantes en un point appelé orthocentre, souvent noté H.
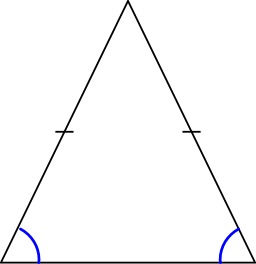
Triangle isocele
Un triangle isocèle est un triangle ayant au moins deux côtés de même longueur. Les deux angles adjacents au troisième côté sont alors de même mesure. Réciproquement, tout triangle ayant deux angles de même mesure est isocèle. Les triangles isocèles sont les seuls à admettre un axe de symétrie en dehors des triangles plats.
Triangle rectangle
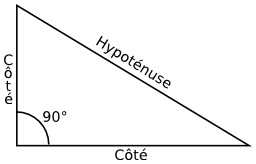
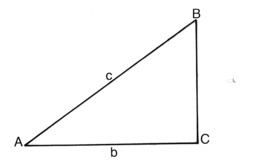
Triangle rectangle : Dans un triangle rectangle, l'hypoténuse (AB) est le côté non adjacent à l'angle droit, ou le côté opposé à l'angle droit (en C).
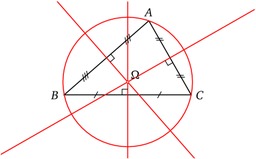
Triangle rectangle
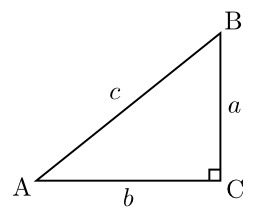
Triangle ABC rectangle en C. Le côté le plus long d'un triangle rectangle est appelé "hypoténuse" (côté AB dans cette image), les deux autres sont les "côtés de l'angle droit". Le théorème de Pythagore énonce, avec les notation du dessin ci-contre, que AB2 = AC2 + BC2.
Triangle rectangle
Triangle rectangle en C dont les côtés sont légendés en français : AB = Hypothénuse ; AC = Côté adjacent à l'angle A ; BC = Côté opposé à l'angle A.
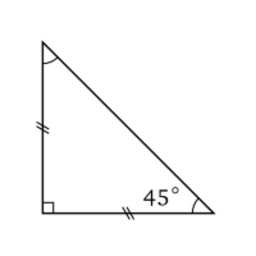
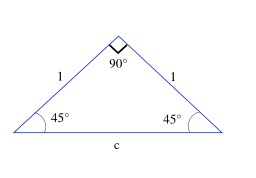
Triangle rectangle isocèle
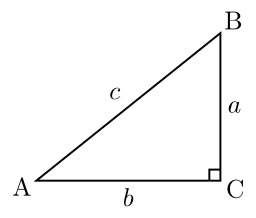
Triangle rectangle isocèle : c = √2. Pour 45 degrés (π/4 radians) : les deux angles du triangle rectangle sont égaux ; les longueurs a et b étant égales, nous pouvons choisir a = b = 1. On détermine alors le sinus, le cosinus et la tangente d'un angle de 45 degrés en utilisant le théorème de Pythagore : c = sqrt{a^2 + b^2} = sqrt{2}. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
Dessins et plans, Géométrie, Jeux mathématiques, Origami, Pliages en papier, Résolution de problème, Trisection de l'angle
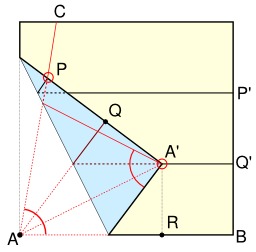
Trisection d'un angle et origami
Trisection de l'angle CAB : résolution d'un problème ne pouvant se faire par la méthode traditionnelle "à la règle et au compas".
Peinture, Géométrie, Raphaêl, Compas, Ardoise, Athènes (Grèce), L' école d'Athènes - Raphaël (1483-1520)
Une leçon d'Euclide
Détail du tableau de Raphaël intitulé "L'école d'Athènes" représentant un mathématicien grec dessinant une construction géométrique avec un compas sur une ardoise posée à terre. Tableau datant de 1509 : Fresque décorant la Chambre de la signature de l'appartement de Jules II au Vatican (une des trois Stanze du musée du Vatican).
Uxmal
Bâtiments de l'ancienne ville d'Uxmal, au Mexique. Le bâtiment du devant est le Quadrilatère des Nonnes et présente les caractéristiques du style Maya de la période Puuc : La mosaïque de pierres et l'importance de Chac, dieu des eaux etdes pluies. On peut voir trois grands masques du dieu au dessus de la porte de droite. En arrière et au dessus, on peut voir la La Pyramide du Devin, l'une des rares pyramides ovales du monde Maya. Sur la pyramide, deux portes sont visibles, la plus basse richement décorée avec des motifs liés à Chac, et la plus haute ayant d'autres motifs Puuc. Au dessus de la porte de gauche, on voit des hauts parleurs utilisés pour des spectacles son et lumière.
Photographie, Géométrie, Vitraux, Métaphore, Triangles (géométrie), Art contemporain, Carlo Roccella (né en 1956), Contribution au vitrail, Art abstrait, Issy-les-Moulineaux (Hauts-de-Seine), Trinité -- Dans l'art
Vitrail moderne à Issy-les-Moulineaux
Vitrail de la Trinité à Issy les Moulineaux, le fils, par Carlo Roccella (né en 1956). Source : http://fr.wikipedia.org/wiki/Carlo_Roccella
Photographie, Géométrie, Bleu, Architecture domestique, Volets, Architecture, Architecture -- Décoration et ornement, Architecture -- Détails, Art roumain, Bucarest (Roumanie), Contrevents
Volets peints à Bucarest
"Fenêtre bleue" aux volets peints de Jurilovca, 1898, au Musée du Village Roumain (Muzeul National al Satului Dimitrie Gusti) de Bucarest : Un contrevent est un dispositif habituellement installé en extérieur devant une fenêtre ou une porte, qui peut être fermé pour se protéger de la lumière, des intrusions, des projectiles, des regards extérieurs ou comme élément d'isolation contre la chaleur, le froid, le vent et la pluie. Il est en général confondu dans le langage courant avec le volet, qui lui est installé en intérieur. Source : http://fr.wikipedia.org/wiki/Contrevent Les contrevents sont traditionnellement composés d'un panneau en bois plein sans fentes avec des gonds métalliques qui les fixent au mur à l'extérieur de la baie (le contrevent battant), ce qui permet de les placer de façon à obstruer l'ouverture. Historiquement, ces contrevents ont pu être des panneaux simplement accrochés par des pitons ; puis ils furent ensuite articulés avec des charnières et rabattus.
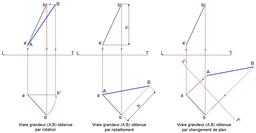
Vraie Grandeur de droite
Vraie grandeur d'une droite obtenue avec la technique dite du changement de plan.