Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Barcelone (Espagne), Astronomes, Dunkerque (Nord), Trigonométrie, Jean-Baptiste Delambre (1749-1822), Pierre Méchain (1744-1804), Télémètres
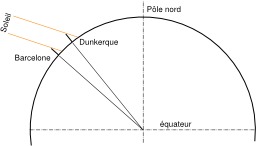
Angle Dunkerque Barcelone
Mesure de l'angle de l'arc de méridien entre Dunkerque (France) et Barcelone (Espagne) en utilisant l'ombre d'un bâton planté à la verticale. Ceci fut fait par des expéditions menées par Delambre et Méchain. Pour mesurer la distance de Dunkerque à Barcelone (qui sont sur un même méridien), on mesura la distance de proche en proche entre des points bien visibles : sommet des églises et des collines. Pour cela, on se place en un point, et on vise l'autre point, selon un principe similaire au télémètre ; la mesure des angles permet de déterminer la distance.
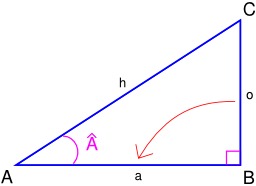
Calcul de la tangente de l'angle A
Représentation géométrique de la tangente dans un triangle rectangle. La tangente d'un angle est le rapport de la longueur du côté opposé à la longueur du côté adjacent :tan(Â) = longueur du côté opposé / longueur du côté adjacent = o/a. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique
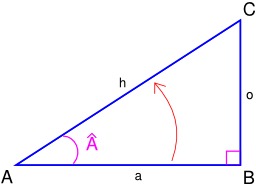
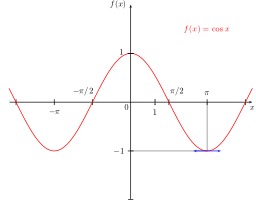
Calcul du Cosinus de l'angle A
Représentation géométrique d'un cosinus dans un triangle rectangle : Le cosinus d'un angle est le rapport de la longueur du côté adjacent par la longueur de l'hypoténuse :cos(Â) = longueur de côté adjacent / longueur de l'hypoténuse = a/h. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique
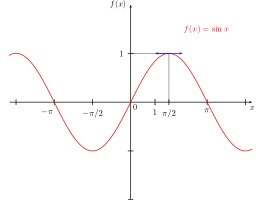
Calcul du Sinus de l'angle A
Représentation géométrique du sinus dans un triangle rectangle. Le sinus d'un angle est le rapport de la longueur du côté opposé par la longueur de l'hypoténuse :sin(Â) = longueur du côté opposé / longueur de l'hypoténuse = o/h. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
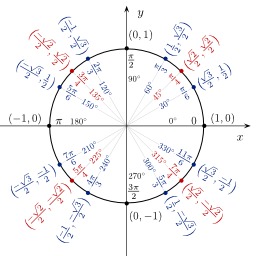
Fonctions trigonométriques dans le cercle unité
Représentation des fonctions trigonométriques dans le cercle unité. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre 0 et π/2. Sur ce cercle sont représentés certains angles communs, et sont indiquées leurs mesures en radians figurant dans l'intervalle [–2π, 2π], soit deux mesures par angle et même trois pour l'angle nul. Notez que les angles positifs sont dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive Ox de l'axe des abscisses coupe le cercle en un point de coordonnées (cos θ, sin θ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
Dessins et plans, Géométrie, Lune, Berlin (Allemagne), Astronomes, Parallaxe, Trigonométrie, Jérôme de La Lande (1732-1807), Le Cap (Afrique du Sud), Nicolas-Louis de La Caille (1713-1762)
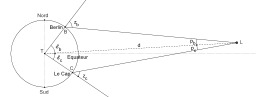
Parallaxe de la Lune entre Berlin et Le Cap
Illustration du calcul de la parallaxe de la lune entre Berlin et Le Cap, par Lalande et Lacaille (étape 2). Durant l'année 1751, Jérôme de La Lande situé à Berlin et Nicolas-Louis de La Caille situé au Cap entreprennent une série de mesures synchrones qui permettront de déterminer avec une relative précision la parallaxe de la Lune. Ils mesurent à des jours fixés la hauteur de la Lune quand celle-ci passe au méridien. La différence de longitude entre ces deux villes est assez faible pour que l'on puisse supposer que la position de la Lune n'a pas significativement changé. La réunion de ces deux mesures permet de déterminer la parallaxe lunaire au moment de l'observation. Lalande trouve ainsi une parallaxe moyenne de 57 minutes et 26 secondes. Le principe en est expliqué par Lalande dans son traité d'astronomie.
Dessins et plans, Coordonnées (mathématiques), Trigonométrie, Courbes algébriques, Fonctions trigonométriques
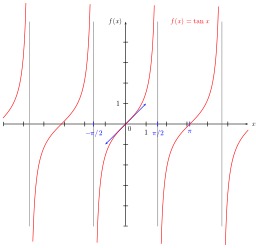
Représentation graphique de la fonction Tangente
Représentation graphique de la fonction Tangente.
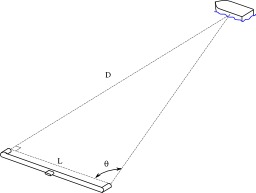
Télémètre à parallaxe
Principe de la mesure au télémètre à parallaxe. La parallaxe est l’incidence du changement de position de l’observateur sur l’observation d’un objet. En d'autres termes, la parallaxe est l'effet du changement de position de l'observateur sur ce qu'il perçoit.
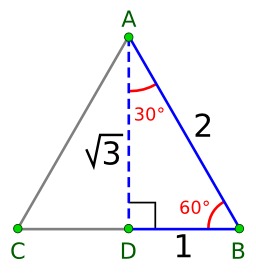
Triangle équilatéral
Représentation géométrique de fonctions trigonométriques : triangle équilatéral divisé en 2 pour calcul du sin, du cos, et de la tan pour 30° et 60°.
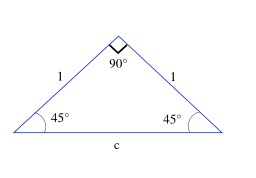
Triangle rectangle isocèle
Triangle rectangle isocèle : c = √2. Pour 45 degrés (π/4 radians) : les deux angles du triangle rectangle sont égaux ; les longueurs a et b étant égales, nous pouvons choisir a = b = 1. On détermine alors le sinus, le cosinus et la tangente d'un angle de 45 degrés en utilisant le théorème de Pythagore : c = sqrt{a^2 + b^2} = sqrt{2}. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.