Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
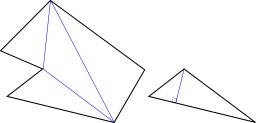
Découpage d'un polygone en triangles
Les triangles ont une importance capitale : en effet, tout polygone — surface délimitée par une ligne brisée fermée — peut se découper en triangles (maillage). Par ailleurs, tout triangle peut se découper en deux triangles rectangles. Ainsi, si l'on sait travailler sur un triangle rectangle, on sait travailler sur tout polygone. Par ailleurs, les triangles rectangles ont des propriétés particulières qui permettent des calculs faciles.
Dessins et plans, Géométrie, Parallèles (géométrie), Thalès, Théorème de, Constructions géométriques, Triangles (géométrie)
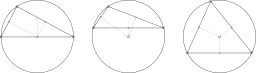
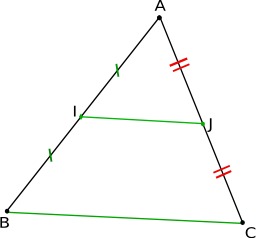
Réciproque du théorème de Thalès
Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès. Si un segment a pour extrémités les milieux de deux côtés d’un triangle, alors il est parallèle au troisième côté, et sa longueur est égale à la moitié de celle de ce troisième côté. Soient I et J les milieux respectifs des segments [AB] et [AC], alors (IJ) // (BC) et IJ = BC ÷ 2.
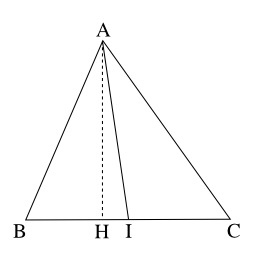
Théorème de la médiane
Médiane et hauteur d'un triangle. Le théorème de la médiane, ou théorème d'Apollonius, est une relation entre la longueur d'une médiane d'un triangle et la longueur de ses côtés. Soit ABC un triangle quelconque, et AI la médiane issue de A. On a alors la relation suivante : AB^2 + AC^2 = 2BI^2 + 2AI^2, Ou encore : AB^2 + AC^2 = {1 over 2} BC^2 + 2AI^2.
Théorème de Stewart
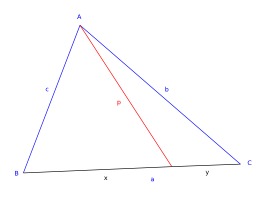
En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane, due au mathématicien Matthew Stewart dans les années 1746 : Théorème — Soit p une cévienne d'un triangle ABC divisant en X le côté a en deux parties x et y. On a alors la relation suivante : acdot (xy+p^{2}) = xcdot b^{2}+ycdot c^{2}. Matthew Stewart est un mathématicien écossais (1717-1785) reconnu comme un mathématicien important après la publication de son "General Theorems", en 1746.
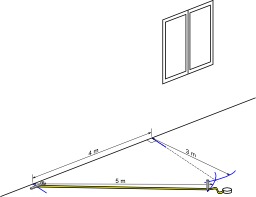
Trace d'une perpendiculaire avec la méthode du 3 4 5
Tracé d'une perpendiculaire en maçonnerie, méthode du 3-4-5 : le triangle est rectangle (théorème de Pythagore).
Triangle rectangle
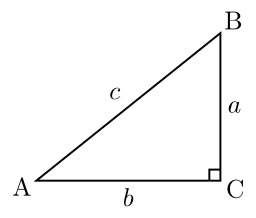
Triangle rectangle : Dans un triangle rectangle, l'hypoténuse (AB) est le côté non adjacent à l'angle droit, ou le côté opposé à l'angle droit (en C).
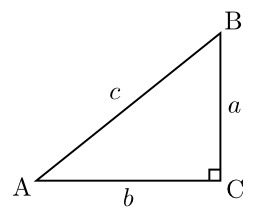
Triangle rectangle
Triangle ABC rectangle en C. Le côté le plus long d'un triangle rectangle est appelé "hypoténuse" (côté AB dans cette image), les deux autres sont les "côtés de l'angle droit". Le théorème de Pythagore énonce, avec les notation du dessin ci-contre, que AB2 = AC2 + BC2.
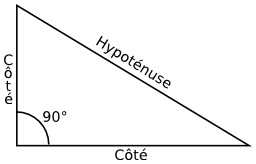
Triangle rectangle
Triangle rectangle en C dont les côtés sont légendés en français : AB = Hypothénuse ; AC = Côté adjacent à l'angle A ; BC = Côté opposé à l'angle A.
Photographie, Géométrie, Vitraux, Métaphore, Triangles (géométrie), Art contemporain, Carlo Roccella (né en 1956), Contribution au vitrail, Art abstrait, Issy-les-Moulineaux (Hauts-de-Seine), Trinité -- Dans l'art
Vitrail moderne à Issy-les-Moulineaux
Vitrail de la Trinité à Issy les Moulineaux, le fils, par Carlo Roccella (né en 1956). Source : http://fr.wikipedia.org/wiki/Carlo_Roccella
Photographie, Vitraux, Métaphore, Triangles (géométrie), Formes (mathématiques), Artistes italiens, Art contemporain, Carlo Roccella (né en 1956), Art abstrait, Issy-les-Moulineaux (Hauts-de-Seine), Iconographie religieuse, Symbolisme des formes
Vitrail moderne à Issy-les-Moulineaux
Vitrail de la Trinité, le père, à Issy les Moulineaux par Carlo Roccella (né en 1956). Source : http://fr.wikipedia.org/wiki/Trinit%C3%A9_chr%C3%A9tienne.