Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
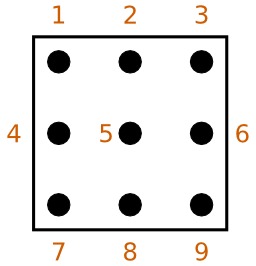
Notation sudoku
Méthode de résolution utilisable par un joueur de sudoku : numéroter les cellules "candidates"
Puzzle d'Euler
Problème d'Euler des 36 officiers : un carré gréco-latin d’ordre 6 est impossible à résoudre. En 1782, le mathématicien suisse Leonhard Euler imagine un problème dans une grille. Certains attribuent donc la paternité du sudoku au Suisse, bien que les travaux d’Euler concernent les carrés latins et la théorie des graphes. On considère six régiments différents, chaque régiment possède six officiers de grades distincts. On se demande maintenant comment placer les 36 officiers dans une grille de 6×6, à raison d’un officier par case, de telle manière que chaque ligne et chaque colonne contienne tous les grades et tous les régiments. Il s’agit en d’autres termes d’un carré gréco-latin d’ordre 6 (la combinaison de deux carrés latins, un carré latin pour les régiments, un carré latin pour les grades), problème dont la résolution est impossible. Euler l’avait déjà pressenti à l’époque, sans toutefois donner une démonstration formelle à sa conjecture. Il dira : « Or, après toutes les peines qu’on s’est données pour résoudre ce problème, on a été obligé de reconnaître qu’un tel arrangement est absolument impossible, quoiqu’on ne puisse pas en donner de démonstration rigoureuse. » En 1901, le Français Gaston Tarry démontre l’impossibilité du résultat grâce à une recherche exhaustive des cas et par croisement des résultats. Le lien entre le sudoku et le problème des 36 officiers est la contrainte qui empêche la répétition du même élément dans la grille, tout en arrivant au final à un jeu qui emploie le principe du carré latin (combinaison de deux carrés latins dans le cas du carré gréco-latin, carré latin subdivisé en plusieurs régions dans le cas du sudoku).