Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Football, Granite, Sphère, Ballons (articles de sport), Sculpture, Art contemporain, Salzbourg (Autriche)
Ballon de foot en pierre à Salzbourg
Ballon de foot en pierre à Salzbourg en Autriche : 2 mètres de diamètre, 2,5 mètres de hauteur, 32 morceaux de granite, par Helmut Moster.
Gravure, Sphère, Dix-septième siècle, Ferronnerie d'art, Objets en fer, Cantines, Économie domestique -- Appareils et matériel, Eugène Viollet-le-Duc (1814-1879), Musée de Cluny. Paris
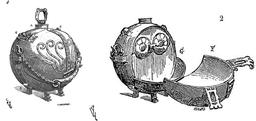
Cantine portable du XVIIème siècle
Dessin d'une cantine portable du XVIIe siècle conservée au musée de Cluny. Fer battu et étamé, 40 cm de hauteur. L'anse supérieure en bronze permet de dévisser le bouchon de l'orifice A) par lequel on introduit de l'eau bouillante dans la moitié de la sphère. Les oreilles C) permettent le passage d'une courroie d'attache. Dans la cantine ouverte (fig. 2), deux disques bouchent des manchons (petits fours) qui peuvent contenir au chaud des viandes cuites. Dans la partie rabattue F) posée sur un brasier, ou dans la poche G) on peut cuire des légumes ou une soupe. Cette coquille fait office de gamelle, mais on peut aussi y loger pain, serviette, couteaux, cuillers et fourchettes. Source : Eugène Viollet-le-Duc (1814–1879), Dictionnaire raisonné du mobilier français de l'époque carolingienne à la Renaissance, t. 2, Paris, 1871, p. 49-51 avec 2 fig.
Dessins et plans, Terre, Sphère, Latitude, Longitude, Géographie, Coordonnées géodésiques, Équateur (géographie), Repérage géographique
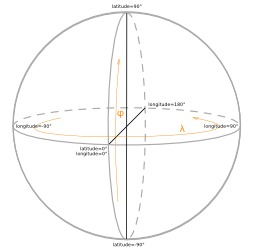
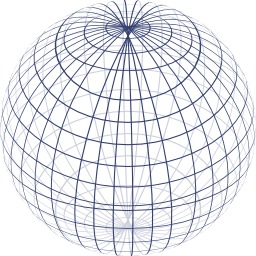
Coordonnées géographiques sur une sphère
Coordonnées géographiques sur une sphère : latitude et longitude.
Dôme sphérique
Dôme de la Grande mosquée de Kairouan. Usage de la sphère en architecture : voûte demi-sphérique côtelée d'un dôme de la Grande Mosquée de Kairouan (en Tunisie).
Photographie, Pierre, Sphère, Sculpture, Parcs géologiques, Réserves naturelles géologiques, Sutherland (GB)
Le globe sculpté en Écosse
Le globe sculpté, oeuvre de Joe Smith à Knockan Crag, Sutherland en Écosse.
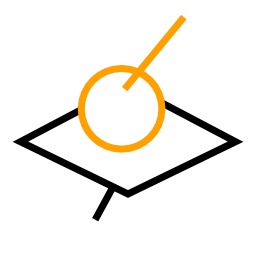
Liaison ponctuelle 3D vectorielle
Schéma d'une liaison ponctuelle sphère/plan dans l'espace : la liaison ponctuelle décrit un contact entre deux solides qui se réduit à un point. Par obstacle, ce contact interdit le rapprochement des deux corps, et autorise la transmission d'une force dans la direction normale (perpendiculaire) au plan tangent commun aux deux surfaces en contact. On définit ainsi son seul degré de liaison. C’est la liaison génératrice de toutes les autres, puisqu’une liaison peut toujours être décrite par plusieurs liaisons ponctuelles, qu'il s'agisse d'un ensemble discret ou continu de points.
Sphère dans un espace euclidien
En géométrie dans l'espace, une sphère est une surface constituée de tous les points situés à une même distance d'un point appelé centre. La valeur de cette distance au centre est appelée le rayon de la sphère. La géométrie sphérique est la science qui étudie les propriétés des sphères.
Photographie, Ponts, Sphère, Géographie, Sculpture, Danube (cours d'eau), Budapest (Hongrie) -- Château
Sphère en pierre à Budapest
Sphère en pierre sur la terrasse de Savoya du Château de Budapest avec vue sur le Danube, Hongrie.
Sphère en pierre précolombienne
Sphère en pierre précolombienne exposée à Harvard University, Cambridge, Massachusetts, USA.
Sphère et bilboquet
Bilboquet pour donner du sens à la sphère : Image de synthèse typique des années 1980 : dallage, sphère, reflets et une image de fond (les nuages).
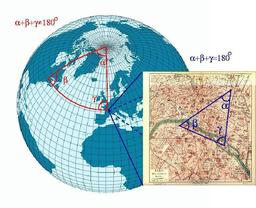
Un triangle sur un globe
Sur une sphère, la somme des angles d'un triangle n'est pas égale à 180° : une sphère n'est pas un espace euclidien. Par contre, les lois de la géométrie euclidienne sont de bonnes approximations locales. Pour un petit triangle sur la surface de la Terre, la somme des angles est proche de 180°.