Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
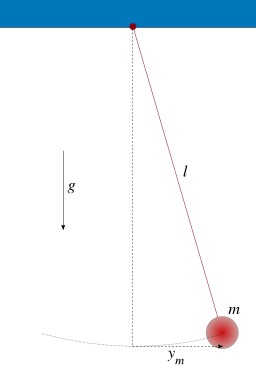
Mouvement pendulaire simple
Schéma montrant le comportement d'un pendule simple : En physique, le pendule est un système oscillant qui, écarté de sa position d'équilibre, y retourne en décrivant des oscillations, sous l'effet d'une force, par exemple la pesanteur. Le mot pendule (nom masculin), dû à Huygens, vient du latin pendere. Le pendule de Foucault est l'un des plus connus. Une petite masse pouvant être assimilée à un point matériel est suspendue au bout d'un fil (ou d'une tige) inextensible et de masse négligeable. Écartée de sa position d'équilibre, puis lâchée, la masse oscille dans un plan, de part et d'autre de la verticale. Cette oscillation provient de l'action de la pesanteur : il s'agit du pendule pesant simple, expression habituellement raccourcie en « pendule simple ». Cet oscillateur, bien que le plus simple, n'est pas un oscillateur harmonique : en particulier, la période des oscillations dépend de l'amplitude du mouvement.
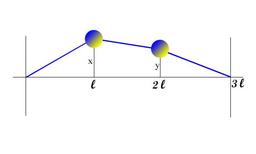
Pendule de D'Alembert
Illustration d'un pendule particulier imaginé par D'Alembert pour modéliser une corde vibrante : La corde vibrante est ici modélisée par un pendule dont la masse est concentrée en deux points régulièrement espacés. Le phénomène physique de la corde vibrante met en relation trois grandeurs physiques : 1) La tension de la corde notée F ; 2) La longueur de la corde notée l ; 3) La fréquence de résonance de la corde notée f.
Pendule électrique
Pendule électrique, attraction électrique. Illustration par Yan Dargent (1824-1899), in Jean Rambosson, Histoire des météores et des grands phénomènes de la nature, Firmin-Didot, 1883 (wikisource).
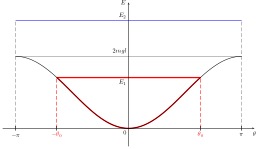
Puits de potentiel pour le pendule simple
Le calcul de l'énergie potentielle puis l'utilisation de l'expression de l'énergie mécanique peut permettre la détermination de l'équation du mouvement du système. Cette méthode est souvent plus judicieuse que l'utilisation du principe fondamental de la dynamique. Méthode énergétique pour la résolution du mouvement du pendule simple : Le système est en équilibre quand son énergie potentielle admet des minimums et des maximums locaux. On peut alors différencier les positions d'équilibre stables et instables selon que l'énergie potentielle est (respectivement) minimale ou maximale. On peut aussi soulever la notion de puits d'énergie potentielle lorsque le graphe de l'énergie potentielle en fonction du paramètre décrivant le mouvement admet un puits. Si le système n'a pas assez d'énergie mécanique pour sortir du puits, il est contraint à rester entre deux positions et peut éventuellement osciller.